ВОЛНЫ В ЦЕНТРИФУГИРОВАННОМ СЛОЕ ВЯЗКОЙ ФЛОТИРУЮЩЕЙ ЖИДКОСТИ, НЕРАВЕНСТВА И СОБСТВЕННЫЕ ФУНКЦИИ ОПЕРАТОРА РОТОР
Автор: Мария Андреевна Свешникова
Соавторы: Солдатов И.Н. , Симакин Д.А.
Организация: Радиофизический факультет ННГУ имени Н.И. Лобачевского, Н. Новгород
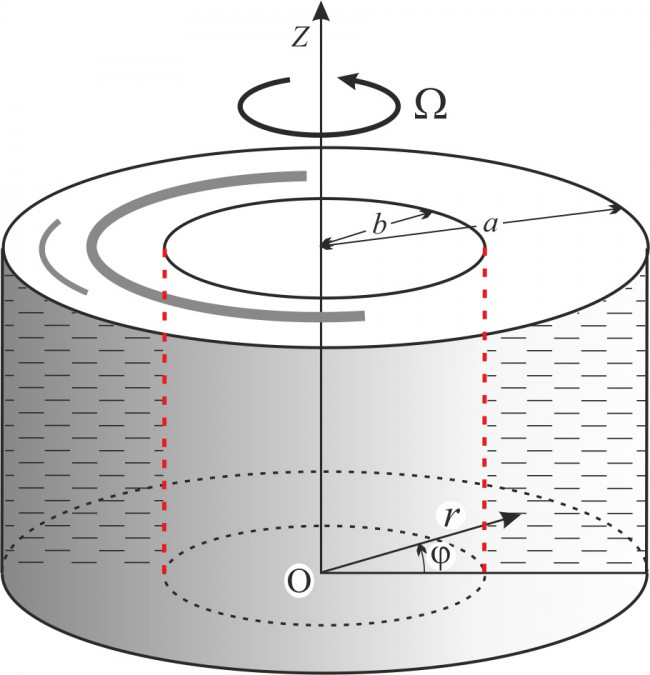
Исследуются основные свойства инерционных (гироскопических) волн во флотирующей вязкой жидкости, образующей центрифугированный слой на твердой стенке цилиндрической полости центрифуги (см. рис.). Наиболее детально рассмотрены азимутальные гироскопические волны. Флотирующая жидкость – это жидкость с инерционной поверхностью, образуемой плавающими на её свободной поверхности и не взаимодействующими между собой частицами, обладающими малой массой. Её движения описываются обычными уравнениями гидродинамики (за исключением того, что в правой части уравнения движения появляются два члена, связанные с действием кориолисовой и центробежной сил, поскольку рассмотрение ведется в неинерциальной системе отсчёта)
(1)
( – динамическая вязкость, – угловая скорость центрифуги, остальные обозначения стандартны), но граничные условия на свободной поверхности являются неклассическими
, ,
где , , , E – число Экмана, – уравнение свободной поверхности, T – вектор, определяющий реакцию частиц инерционной поверхности, в цилиндрической системе координат имеет вид
.
В отличие от традиционного подхода с применением погранслойных функций при решении задач с малым параметром при старших производных, мы ищем не приближенное, а точное решение гидродинамической задачи. Для построения решения используется суперпозиция собственных функций несамосопряженного оператора rot. Собственные вектор-функции v(x) оператора в пространстве соленоидальных полей, определяются из несамосопряженной задачи на собственные значения в двусвязной области. Получено и исследовано дисперсионное уравнение. Показано, инерционная поверхность оказывает дестабилизирующее действие. Получены оценки параметров, при которых стационарное движение жидкости является устойчивым.
