НИИ механики МГУ имени М.В. Ломоносова, биологический факультет МГУ имени М.В. Ломоносова
В работе [1] описано разработанное в НИИ механики МГУ устройство, позволяющее формировать длинную (длиной ~ 5D) ламинарную струю диаметром D = 0.12 м при числах Рейнольдса около 10 000. Особенность устройства состоит в том, что его длина составляет всего 1.5D. Для формирования струи диаметра ~ 0.1 м стандартным способом понадобилась бы труба длиной десятки метров (в ней на выходе формируется параболический профиль скорости, благодаря которому затопленная струя остаётся ламинарной на расстоянии нескольких диаметров от выхода из трубы) [3]. Полученная в работе [1] струя позволила экспериментально верифицировать предсказания линейной теории устойчивости в применении к затопленной струе круглого поперечного сечения [2], что является вкладом в развитие фундаментальной теории устойчивости.
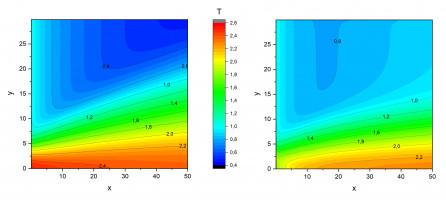
Кроме этого, разработанный способ создания длинных ламинарных струй имеет непосредственное прикладное значение. Если сформировать струю достаточно большого диаметра, состоящую из очищенного воздуха, то она может быть использована в качестве локальной чистой зоны. Такие зоны необходимы в ряде областей высокоточной промышленности, медицине, биологических и химических лабораториях. Если зона создаётся с помощью ламинарной струи, она не должна быть отгорожена непроницаемыми стенками, отсутствие которых упростит доступ персонала к защищаемому объекту и облегчит работу с ним. В докладе рассказывается об установке (см. рис. 1(а)), создающей локальную чистую зону диаметром 0.5 м и длиной 0.8 м. Кроме измерений механических характеристик струи, совместно с лабораторией физиологии и биохимии микробов биологического факультета МГУ проведены микробиологические эксперименты, результаты которых подтверждают, что струя очищенного воздуха не смешивается с окружающим воздухом, специально загрязнённым микроорганизмом Bacillus subtilis в споровом состоянии, и остаётся ламинарной на расстоянии до 0.8 м (см. рис. 1(б – г)).
Работа частично поддержана грантом РФФИ (проект № 18-08-00074).
Рис. 1: а — схема устройства, формирующего ламинарную струю, на штативе и расположение чаш Петри с питательной средой на рабочем столе (эксперименты проводились для различных расстояний L); на чашах, стоявших на расстоянии L = 0.8 м от диффузора при проведении эксперимента по загрязнению окружающего воздуха, не обнаружено колониеобразующих единиц (КОЕ) (б); на чашах, стоявших на расстоянии L = 1.2 м, выявлено 3.48 КОЕ/см2 (в); на контрольной чаше, стоявшей вдали от струи очищенного воздуха, выявлено 28 КОЕ/см2 (г).
1. Zayko J., Teplovodskii S., Chicherina A., Vedeneev V., Reshmin A. Formation of free round jets with long laminar regions at large Reynolds numbers. Phys. Fluids. 2018. V. 30. 043603.
2. Zayko J., Reshmin A., Trifonov V., Gareev L., Vedeneev V. Experimental study of perturbation growth in the submerged jet. EDRFCM 2019. March 26–29 2019, Bad Herrenalb, Germany.
3. Козлов Г.В., Грек Г.Р., Сорокин А.М., Литвиненко Ю.А. Влияние начальных условий на срезе сопла на структуру круглой струи. Теплофизика и аэромеханика. 2008. Т. 15. № 1. С. 59 – 73.
Юлия Сергеевна Зайко
НИИ механики МГУ
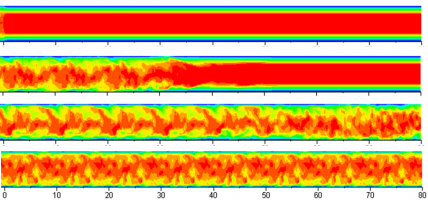
Турбулентные течения характеризуются пульсациями гидродинамических полей со случайным поведением, как во времени, так и в пространстве. При численном моделировании пространственно развивающихся течений в рамках уравнений Навье-Стокса требуется задание некоторого поля скорости во входном сечении в каждый момент времени. Например, в трубах входное течение можно задавать в виде суперпозиции равномерного потока либо течения Пуазейля и некоторого нестационарного возмущения. Развитие возмущения вниз по потоку при достаточно больших числах Рейнольдса приводит в конечном итоге к установлению развитой турбулентности с постоянными по длине трубы средними характеристиками. В зависимости от вида входных условий для установления течения может потребоваться значительная длина в несколько десятков или даже сотен калибров. Для ускорения выхода течения на установившийся режим предложено несколько стратегий формирования нестационарного входного потока со случайными во времени пульсациями и частотными характеристиками близкими к характеристикам развитой турбулентности. Предполагается, что чем ближе распределение по сечению трубы частотного состава пульсаций на входе к установившемуся течению, тем быстрее (на меньшей длине) будет достигаться установление. Отметим, что пространственные (по длине трубы) формы развивающегося течения никак при этом не прогнозируются. Бытует неявное предположение, что случайные во времени пульсации вызывают случайные же распределения в пространстве.
В докладе будет показано, что предположение о неминуемой пространственной случайности пространственно развивающегося турбулентного течения ошибочно. Аналитически построен алгоритм формирования входных граничных условий, дающих установившееся по длине трубы строго периодическое турбулентное течение с заранее заданным периодом [1]. Средние характеристики в этом течении на всей длине, начиная с входного сечения, постоянны и согласуются со всеми хорошо установленными экспериментальными данными.
Подпись к иллюстрации:
Замещение исходно ламинарного течения Пуазейля в трубе пространственно-периодическим турбулентным течением с периодом L=10 под действием входных возмущений, Re=4000. Поле продольной компоненты скорости в последовательные моменты времени. Течение слева направо.
Численно показано, что хотя построенное решение неустойчиво, и возмущения экспоненциально нарастают вниз по потоку, отклонение от чистой периодичности может оставаться на уровне менее 1% на длинах до 100 радиусов трубы.
Работа выполнена с использованием оборудования Центра коллективного пользования сверхвысокопроизводительными вычислительными ресурсами МГУ имени М.В. Ломоносова при поддержке гранта РНФ № 18-71-10075.
1.Nikitin N. Spatial periodicity of spatially evolving turbulent flow caused by inflow boundary condition // Phys. Fluids. 2007. V. 19. № 9. P. 091703(4).
Николай Васильевич Никитин
НИИ механики МГУ имени М.В. Ломоносова
Ранее была построена модель течения смеси газа и заряженных частиц с учётом их взаимодействия и электризации. В качестве взаимодействия частиц рассматривалось их соударение, в результате которого скорости и заряды частиц изменяются. Заряд, передаваемый при ударе, зависит от упругих и электрических свойств материала частиц, их размеров и скоростей. Удар рассматривался как абсолютно упругий, трение между частицами не учитывалось. В этой работе соударение частиц рассматривается как неупругий удар с ненулевым коэффициентом восстановления (когда коэффициент восстановления равен 1, удар является абсолютно упругим). Предполагается, что частицы не коагулируют (случай абсолютно неупругого удара). Учитывается трение между частицами и их вращение. Проводится оценка учёта дополнительных факторов взаимодействия частиц на течение смеси.
1. Горохова Н. В. Эволюция электрического поля в течениях смеси газа с заряженными частицами // XII Всероссийский съезд по фундаментальным проблемам теоретической и прикладной механики: сборник трудов в 4 томах. РИЦ БашГУ Уфа, 2019. Т. 4. С. 31–33.
2. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика – Том 7. Теория упругости. М: Наука. 1987.
3. Soo S.L. Dynamics of charged suspensions // International reviews in aerosol physics and chemistry. Vol. 2. Pergamon Press, Oxforf. 1971. P. 61-149.
Наталья Владимировна Горохова
Институт теоретической и прикладной механики им. С.А. Христиановича СО РАН
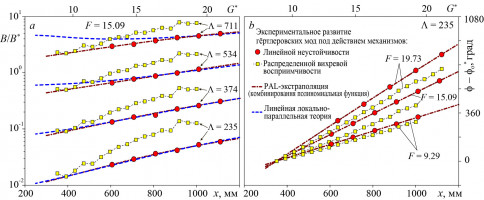
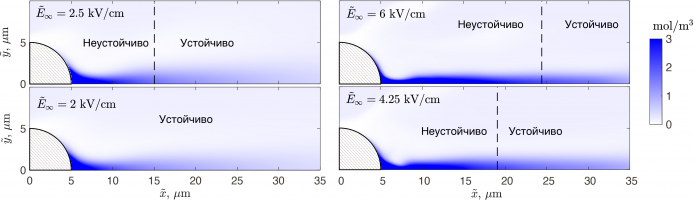
Работа посвящена систематическому экспериментальному исследованию одного из наиболее эффективных механизмов порождения нестационарных (в общем случае) вихрей Гёртлера [1], связанного с распределенным рассеянием низкочастотных и стационарных вихрей набегающего потока на естественной неоднородности нарастающего пограничного слоя. Эксперименты проведены в малотурбулентной аэродинамической трубе Т-324 ИТПМ СО РАН при скорости основного потока 9,18 м/с в двумерном пограничном слое типа Блазиуса на вогнутой поверхности высокоточной экспериментальной модели (радиус закругления R = 8,37 м). Основные измерения выполнены термоанемометром с использованием метода контролируемых нестационарных возмущений, реализованного за счет применения специальных источников. Прямые экспериментальные результаты получены для вихрей Гёртлера трех частот f = 8, 13 и 17 Гц (частотный параметр F = 9,29; 15,09 и 19,73) с поперечными длинами волн λz = 7 ÷ 24 мм (безразмерный поперечный масштаб L = 119 ÷ 758) в диапазоне чисел Гёртлера G*= 8,6 ÷ 21,0.
Обнаружено, что исследуемый механизм распределенной вихревой восприимчивости способен эффективно порождать как стационарные, так и нестационарные вихри Гёртлера, а также существенно модифицировать законы развития нестационарных (по крайней мере) гёртлеровских мод вниз по потоку (рис. 1). Действие механизма способно сильно изменять инкременты возмущений пограничного слоя и обеспечивать как усиление, так и подавление нестационарных гёртлеровских мод. В работе получены оценки количественных характеристик исследуемой задачи – коэффициентов распределенной вихревой восприимчивости. Найдено, что амплитуды и фазы коэффициентов не зависят от продольной координаты (в исследованном диапазоне параметров) и являются постоянными величинами (константами). Амплитуды коэффициентов нарастают (по линейному закону) с ростом частоты возмущений, а также с ростом их поперечного масштаба (особенно в области высоких частот). Оценки коэффициентов при порождении стационарных вихрей Гёртлера были получены путем линейной аппроксимации частотной зависимости амплитуд коэффициентов при порождении нестационарных гёртлеровских вихрей с последующей экстраполяцией на нулевую частоту. Обнаружено, что ответственный за порождение стационарных мод неустойчивости Гёртлера механизм распределенной вихревой восприимчивости является значительно более слабым, чем в случае порождения нестационарных гёртлеровских вихрей.
1.Boiko A.V., Ivanov A.V., Kachanov Y.S., Mischenko D.A. Steady and unsteady Görtler boundary-layer instability on concave wall // European Journal of Mechanics B/Fluids, 2010, 29, 61-83.
Дмитрий Алексеевич Мищенко
ИФТТ РАН, ИТФ РАН
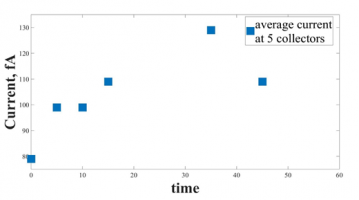
На рисунке: Зависимость суммарного тока от времени. Usours=350В,Uside1=6В,Uside2=6В,Uup=5В,Udown=25В, Freq=13Гц,A=10В
Вихревое движение может быть создано волнами на поверхности жидкости. При движении двух неколлинеарных волн под углом друг к другу формируется решетка вихрей.[1] Первоначально эксперименты по генерации вихрей волнами проводились на воде. Однако в природе, помимо классических жидкостей, существуют и квантовые жидкости, в которых вихревое движение квантовано. К таким жидкостям относится гелий-4 при температуре ниже 2,17 К. При температурах около 1,3 К плотность сверхтекучей компоненты доминирует. Инжектированные заряды являются хорошими пробными частицами для изучения вихревых течений в сверхтекучей жидкости, поскольку они взаимодействуют с квантовыми и нормальными вихрями[2].
Основной целью данной работы является изучение формирования квантовых вихревых структур поверхностными волнами в широком диапазоне температур, а также изучение эволюции вихревых структур при изменении условий накачки волн. Исследования проводились в гелиевой ячейке, находящейся в гелиевом криостате. В ходе эксперимента измерялся ток, приходящий на сборный коллектор. Волны на поверхности возбуждались двумя перпендикулярными плунжерами.
Чтобы оценить поведение вихревой структуры после отключения накачки, мы измерили временную зависимость величины общего тока, поступающего на все 5 сегментов. Точки на рисунке демонстрируют результаты измерений, выполненных через 0, 5, 10, 15, 35, 45 минут после выключения откачки. Видно, что суммарный ток линейно увеличивается со временем примерно на 30%. Можно предположить, что доля зарядов не достигла коллекторов из-за взаимодействия с вихрями. По-видимому, в результате взаимодействия заряды могут отклоняться от прямой траектории и перемещаться к боковым граням.
Разработан метод исследования поведения вихревой системы в сверхтекучем гелии-4 с помощью инжектированных зарядов. Первые эксперименты показывают, что волны на поверхности сверхтекучего гелия генерируют вихри, которые проникают в объем. В будущих экспериментах мы планируем более детально изучить взаимодействие зарядов с квантовыми вихрями.
Работа выполнена при поддержке гранта Министерства науки и высшего образования РФ #075-15-2019-1893
1. S.V. Filatov, V.M. Parfenyev, S.S. Vergeles, M.Y. Brazhnikov, A.A. Levchenko, V.V. Lebedev // Physical Review Letters. – 2016. – V. 116. – I. 5. – P. 054501.
2. P. M. Walmsley, A. I. Golov, H. E. Hall, A. A. Levchenko, and W. F. Vinen, PRL 99, 265302 (2007)
Мадина Рафаиловна Султанова
Механико-математический факультет МГУ имени М. В. Ломоносова, Москва
В работе рассматриваются течения вязкоупругой жидкости между двумя параллельными пластинами на малом расстоянии друг от друга – так называемые течения в ячейке Хеле-Шоу. Вязкоупругие свойства описываются моделью Максвелла с верхней конвективной производной. Модель характеризуется двумя постоянными параметрами: сдвиговой вязкостью и временем релаксации напряжений. Осреднением общей трёхмерной модели по координате, перпендикулярной пластинам ячейки Хеле-Шоу, получается двумерная модель фильтрации жидкости Максвелла. Частными случаями полученных уравнений являются уравнения Дарси и Бринкмана с учётом времени релаксации. При времени релаксации, стремящемся нулю, уравнения фильтрации жидкости Максвелла переходят в обычные уравнения Бринкмана для ньютоновской жидкости.
Изучается вытеснение вязкоупругой жидкости из ячейки Хеле-Шоу. Проведён линейный анализ устойчивости плоского фронта вытеснения вязкоупругой жидкости другой вязкоупругой жидкостью. Важная особенность исследования – отсутствие в системе стабилизирующего фактора – поверхностного натяжения. В его отсутствие, характерный размер неустойчивости определяется вязкими нормальными напряжениями: классическое динамическое условие равенства давлений на межфазной границе заменяется более общим равенством нормальных напряжений. Линейный анализ показал, что при определённом соотношении времён релаксации возможен «резонанс» – резкое увеличение темпа роста малого возмущения на фронте вытеснения. Это увеличение может приводить к образованию упругих трещин.
Олег Анатольевич Логвинов
НИИ механики МГУ, Москва
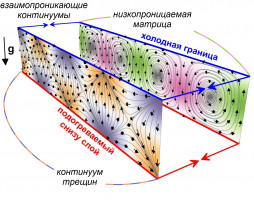
Рис. Схема постановки двухмерной задачи. Показаны линии тока в трещинах и низкопроницаемой матрице.
Исследуется свободная конвекция в трещиновато-пористой среде, т.е. среде, содержащей высокопроницаемые трещины (или каналы), вмещенные в низкопроницаемую матрицу – однородную среду с микро-пористостью. Фильтрация в подобных средах осложняется нарушением локального теплового равновесия между трещинами и матрицей. Влияние неравновесного характера течения на конвекцию исследуется в классической постановке Рэлея—Бенара [1], описывающей развитие ячеистой конвекции в подогреваемом снизу горизонтальном слое насыщенной трещиновато-пористой среды (Рис.).
Для описания течений используется модель двойной пористости и проницаемости, построенная с использованием двух взаимопроникающих континуумов. Один континуум соответствует трещинам, а второй – блокам. В каждой из этих сред тепломассобмен описывается системой законов сохранения и законом Дарси. Учитывается как кондуктивный, так и конвективный теплообмен между средами. Показано, что в такой двойной среде критическое число Рэлея зависит только от трёх параметров подобия, характеризующих распределение коэффициентов проницаемости и теплопроводности между трещинами и матрицей, а также параметра, описывающего интенсивность тепломассообмена между континуумами.
В линейном приближении исследованы решения дисперсионного уравнения, описывающего условия развития конвекции. Обнаружена богатая картина режимов конвективных течений. В зависимости от параметров среды и граничных условий существуют режимы как с совпадающим, так и противоположным направлением течения в трещинах и матрице (Рис.). Течение может перестроится в режим «плоской» конвекции, в котором нагретая жидкость поднимается только по трещинам, а холодная жидкость опускается по матрице. Показано, что в определенном диапазоне параметров именно тепломассобмен между континуумами, а не внутри них, приводит к потере устойчивости стратификации жидкости и развитию конвекции. Подробно описана диаграмма решений при малой степени надкритичности. Важный для практических приложений вывод заключается в том, что неоднородность пористой среды, например, связанная с трещиноватостью, всегда понижает запас устойчивости тепловой стратификации жидкости. Проведено численное моделирование фильтрации, подтвердившее результаты аналитического исследования дисперсионного уравнения.
Работа выполнена в рамках проекта МД-3567.2018.1 Совета по грантам Президента РФ.
1. Nield, D. A. & Bejan, A. Convection in porous media, 5th edn. New York, 2017. NY: Springer.
Андрей Александрович Афанасьев
НИИ механики МГУ им. М.В. Ломоносова
Рассматривается сверхзвуковое течение двухкомпонентной смеси «газ-капли» в плоском линейно расширяющемся канале с теплоизолированными стенками. Задача состоит из двух частей: в первой исследуется невязкий двухфазный поток вдали от стенки с целью найти такие соотношения определяющих параметров, которые соответствуют наиболее интенсивному росту капель благодаря процессу конденсации. Вторая часть – исследование движения капель и межфазного теплообмена в пограничном слое на стенке канала. Цель работы – определить, насколько возможно снижение равновесной температуры теплоизолированной стенки из-за наличия в потоке дисперсной фазы.
Для исследования характера газокапельного потока используется двухконтинуальная модель с фазовыми переходами на поверхности капель [1]. Считается, что во всей рассматриваемой области температура жидкости на поверхности и внутри капель не меняется. Для определения параметров потока вдали от пластины решаются квазиодномерные невязкие уравнения двухфазной среды с учетом обратного влияния и процесса конденсации. Установлено, что наиболее интенсивный рост капель происходит при малых значениях относительной массовой концентрации капель, а также при больших значениях параметра расширения канала.
Для исследования течения вблизи стенки используются уравнения теории двухфазного ламинарного пограничного слоя с малой объемной долей жидкой фазы [2]. В межфазном обмене импульсом, помимо силы аэродинамического сопротивления, учитывается боковая сила Сэфмана, под воздействием которой капли могут выпадать на обтекаемую поверхность. Уравнения двухфазного пограничного слоя решаются численно методом прогонки. Для численного интегрирования уравнений используется неявная разностная схема с первым порядком аппроксимации по продольной координате и вторым порядком - по поперечной.
В результате численных расчетов построены поля параметров фаз, такие как температура газа, размер и концентрация капель, а также графики изменения равновесной температуры стенки. На рисунке приведены картины распределения температуры несущей фазы в пограничном слое для чистого газа и газа с примесью капель. Во втором случае наблюдается охлаждение газа вблизи стенки по сравнению со случаем чистого газа.
1. Marble F.E. Dynamics of dusty gases // Annu. Rev. Fluid Mech. 1970. V. 2. P. 397-446.
2. Osiptsov A.N. Mathematical modeling of dusty-gas boundary layers // Appl. Mech. Rev. 1997. V. 50. P. 357-370.
Ирина Валерьевна Голубкина
Институт механики сплошных сред ПФИЦ УрО РАН

Стремительный процесс урбанизации приводит к бурному изменению морфологии городской застройки и оказывает негативное влияние на микроклимат в пределах городского ландшафта. Проблема прогнозирования микроклимата на масштабах города на сегодняшний день не решена. Городской микроклимат в первую очередь связан с естественной циркуляцией воздуха, интенсивность которой зависит от геометрии городского пространства и особенностей рельефа местности. Прямое численное моделирование городской среды, даже при помощи современных суперкомпьютеров, не представляется возможным. Создание двумерных моделей бессмысленно, течения в такой системе принципиально трехмерные. Существующие трехмерные модели с более подробной детализацией сильно ограничены по масштабам и требуют больших вычислительных ресурсов [1-2]. При этом результаты трехмерного моделирования согласуются с данными натурных наблюдений только при сравнении средних характеристик. В свою очередь натурные эксперименты дают очень ограниченный набор данных и чаще всего используются только для верификации моделей. Разумной альтернативой используемым подходам может служить лабораторный эксперимент. Однако экспериментальных работ по городской климатологии очень мало [3-4].
Целью данного исследования является лабораторное моделирование процессов теплообмена за счет нагрева поверхности города солнечным излучением. В качестве объекта исследования был использован трехмерный макет части города Пермь, который учитывает сложный рельеф местности, высоту и расположение зданий на территории площадью 5 квадратных километра (макет создан в масштабе 1:4000). Рассмотрено влияние рельефа на величину и пространственное распределение конвективного теплопотока при наличии и отсутствие внешней циркуляции.
Работа выполнена при поддержке Правительства Пермского края (проект № С-26/788)
1. Cybyk B. et al. Simulation of fluid dynamics around complex urban geometries // 39th Aerospace Sciences Meeting and Exhibit. 2001. 803
2. Boris, J. The threat of chemical and biological terrorism: preparing a response // Computing in Science & Engineering. 2002. 4(2). 22-32.
3. Kastner-Klein P., Rotach M. W. Mean flow and turbulence characteristics in an urban roughness sublayer //Boundary-Layer Meteorology. 2004. 111(1). 55-84.
4. Klein P., Leitl B., Schatzmann M. Driving physical mechanisms of flow and dispersion in urban canopies //International Journal of Climatology: A Journal of the Royal Meteorological Society. 2007. 27(14). 1887-1907.
Анна Валерьевна Евграфова
МГУ имени М.В. Ломоносова
Существует множество работ, посвящённых движению и устойчивости упругих трубок с текущей внутри жидкостью, которые находят приложения в ядерной энергетике, системах охлаждения и биомеханике. Исследовались как «жёсткие» трубки, теряющие устойчивость в форме изгибных колебаний [1, 2], так и «мягкие» [3], в которых происходят схлопывания поперёк сечения. В последнее десятилетие растёт интерес к стационарным и движущимся солитонам, которые могут возникать в трубках с текущей жидкостью [4, 5], поскольку они могут описывать возникновение аневризм кровеносных сосудов человека и животных. Ранее такие исследования проводились в предположении, что движущаяся жидкость идеальна.
В настоящей работе уравнения движения геометрически и физически нелинейной мембранной трубки с протекающей жидкостью, полученные в [4], обобщаются на случай вязкой и, вообще говоря, неньютоновской жидкости в предположениях [6, 7]. С помощью этой системы изучаются солитоноподобные решения в бесконечных, полубесконечных и конечных мембранных трубках из несжимаемого гиперупругого материала Гента.
При движении вязкой жидкости в бесконечно длинной трубке доказано существование двух предельных состояний при x® –∞ и x® +∞ таких, что деформации стремятся к конечным значениям, а напряжения — к бесконечности, так чтобы компенсировать бесконечно растущее вверх по потоку (и бесконечно убывающее вниз по потоку) давление и растягивающую силу. Найден диапазон скоростей, в котором существует монотонный переход от одного состояния к другому в «центральной» части трубки (т.е., решение для всей трубки в целом). Доказано, что солитоноподобных решений не существует. Однако, такие решения существуют, если трубка неограниченна только в одном направлении, либо вверх, либо вниз по потоку. Решений в виде повторяющихся волн в таких трубках по-прежнему нет. Для трубок конечной длины существуют как солитоноподобные решения, так и решения в виде повторяющихся волн.
Работа поддержана грантом РФФИ 18-29-10020.
1.Paidoussis, M.P. Fluid-structure interactions: slender structures and axial flow. V. 1. Acad. press, 1998.
2.Горшков А.Г., Морозов В.И., Пономарёв А.Т., Шклярчук Ф.Н. Аэрогидроупругось конструкций. М.: Физматлит, 2000.
3.Heil, M., Hazel, A.L. Fluid-Structure Interaction in Internal Physiological Flows. Ann. Rev. Fluid Mech. V. 43, p. 141-162, 2011.
4. M. Epstein, C. R. Johnston. On the exact speed and amplitude of solitary waves in fluid-filled elastic tubes. Proc. R. Soc. Lond. A. 2001. Vol. 457. P. 1195–1213.
5.Y.B. Fu, A.T. Ilichev. Solitary waves in fluid-filled elastic tubes: existence, persistence, and the role of axial displacement. IMA Journal of Applied Mathematics. 2010. Vol. 75. P. 257--268.
6. А. Б. Порошина, В. В. Веденеев. Существование и единственность стационарного состояния упругой трубки при протекании через нее степенной жидкости// Российский журнал биомеханики. 2018. Т. 22. № 2. P. 196-222.
7.В. В. Веденеев, А. Б. Порошина. Устойчивость упругой трубки, содержащей текущую неньютоновскую жидкость и имеющей локально ослабленный участок// Труды МИАН. 2018. Т. 300. С. 42-64.
Василий Владимирович Веденеев
Финансовый университет при Правительстве Российской Федерации
Одной из фундаментальных проблем при проектировании лабораторий на чипе для медицинской диагностики является проблема малых концентраций аналита в микропробах. Большинство биологических пептидов и макромолекул имеют очень низкую концентрацию в пробах, поэтому для их детектирования необходимо предварительное локальное концентрирование. В экспериментальной работе [1] наблюдался эффект суперконцентрации, когда на полюсе ионоселективной микросферы наблюдалось увеличение концентрации пептидов.
Наши теоретические работы [2,3] по исследованию электрофореза ионоселективной микросферы качественно подтвердили этот результат и показали, что за микрогранулой при достаточно большой напряженности внешнего электрического поля образуется зона повышенной концентрации соли. С учётом движения микрогранулы, за ней образуется концентрационный след, распространение которого имеет автомодельный характер.
Концентрационный след за частицей, несмотря на электронейтральность, вызывает остаточный заряд, так как порождает неоднородность электрической проводимости электролита. В результате при достаточно большой напряженности поля концентрационный след может терять устойчивость вблизи микрогранулы, где градиент концентрации наибольший. Возникающие неоднородности переносятся вдоль по потоку. В упрощенной постановке получено стационарное автомодельное решение и проведен линейный анализ его устойчивости.
Качественно такой механизм неустойчивости похож на электрокинетическую неустойчивость, вызванную градиентом концентрации [4].
1. Wang S.-C. и др. Dynamic superconcentration at critical-point double-layer gates of conducting nanoporous granules due to asymmetric tangential fluxes. // Biomicrofluidics. 2008. Т. 2. № 1. С. 14102.
2. Frants E.A., Ganchenko G.S., Shelistov V.S., Amiroudine S., Demekhin E.A. Nonequilibrium electrophoresis of an ion- selective microgranule for weak and moderate external electric fields // Physics of Fluids. 2018. Vol. 30, No 2. P. 022001.
3. Ganchenko G., Frants E., Shelistov V., Nikitin N., Amiroudine S., Demekhin E. Extreme nonequilibrium electrophoresis of an ion-selective microgranule // Phys. Rev. Fluids, 2019. Vol. 4, No 4. P. 043703.
4.Chen C.-H. и др. Convective and absolute electrokinetic instability with conductivity gradients // J. Fluid Mech. 2005. Т. 524. С. 263–303.
Георгий Сергеевич Ганченко
НИИ Механики МГУ
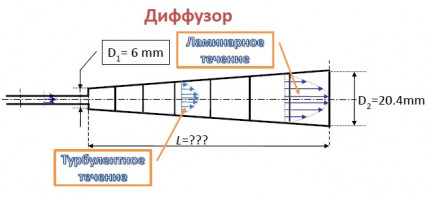
В работе исследовалось явление ламинарно-турбулентного перехода в диффузоре в зависимости от угла раскрытия и степени расширения канала (отношения входного диаметра диффузора к выходному). При расчете использовалась трехпараметрическая модель сдвиговой турбулентности [1]. Расчеты проводились, при числах Рейнольдса на входе в канал от 100 до 4000. На вход в диффузор подавалось, либо развитое турбулентное течение, либо течение с равномерным профилем скорости и с разной энергией турбулентности. Угол раскрытия варьировался от 0.01° до 4°, при этом течение в канале происходило, при положительном, отрицательном или нулевом продольном градиенте давления. Полученные при расчете характеристики течения на выходе диффузора и различных сечениях вдоль диффузора сравнивались с экспериментальными данными [2]. При заданном угле раскрытия и степени расширения, течение в диффузоре зависит только от локального числа Рейнольдса и не зависит от условий на входе, пока эти условия достаточны для формирования турбулентного течения. Было показано, что при увеличении длины диффузора турбулентное течение затухает и плавно переходит в ламинарное.
Получены рис. а зависимости критического числа Рейнольдса от угла раскрытия для диффузоров с разной степенью расширения 1.65, 2.5, 3.4 и 6.8 (обозначение индексов: 1 - вход в диффузор, 2 - выход из диффузора). При угле раскрытия 0.01°, что очень близко к прямой круглой трубе, критическое число Рейнольдса для заданных степеней расширения лежит в диапазоне от ~900 до ~1000. Также получены зависимости рис. б критического числа Рейнольдса от угла раскрытия со степенью расширения канала 3.4 и разной энергией турбулентности на входе в диффузор.
В докладе будет рассмотрен вопрос как влияет степень расширения канала на величину генерации турбулентного течения. Также будут представлены изменения энергии турбулентности по сечению диффузора за счет переноса, генерации, диссипации и диффузии турбулентного течения.
Владимир Викторович Трифонов
Институт физики атмосферы им.А.М.Обухова РАН
Эмиссия частиц микронного и субмикронного размера связывается с наличием потока сальтирующих частиц [1], усиливается с увеличением высоты эффективной шероховатости [2] и имеет кубическую зависимость от динамической скорости [3]. Другой механизм выноса связан с возникновением тепловых конвективных потоков над поверхностью [4]. Соотношение доли падающих частиц к частицам, выносимым с поверхности, возрастает при движении вверх по наветренному склону дюны [5, 6]. Этот факт позволяет сделать вывод о преобладании вертикального механизма выноса частиц над сальтационным (ударным). Проведены исследования условий отрыва отдельных частиц и влияния на этот процесс возникновения и роста эоловых микроструктур.
Рассмотрено обтекание микроряби высотой 0,1-1 мм при скоростях воздушного потока до 4 м/с на высоте 1-2 см с использованием открытого пакета LES model in openFOAM. Добавление на шероховатую поверхность обтекаемой эоловой структуры борозд у вершины приводит к смещению точки отрыва восходящих потоков, к изменению протяженности зоны рециркуляции и временных интервалов струйного усиления ветра у вершины, которое наблюдалось в частности в [7]. Эксперимента с добавлением борозды добавлены с учетом численных исследований для обтекания отдельных частиц для области 5х5х2 мм при скорости воздушного потока на верхней границе 2,8 м/с, выбираемой в соответствии с данными экспериментов в ветровом канале [7]. В зависимости от расстояния между частицами меняются выталкивающая сила, действующая со стороны воздушного потока, критическая скорость и начальные скорости вылета частицы. Как следствие, появляются области с различной вероятностью ветрового выноса, за счет чего, в частности, возникает эоловая рябь.
Исследование выполнено при поддержке проекта РНФ 20-17-00214.
- Houser C. A., Nickling W. G. Sedimentology. 2001. 48(2). 255-267.
- Martin R.L., Kok J.F. J. Geophys. Res. 2018. 123(7). 1546-1565.
- Shao Y., Raupach M. R., Findlater P. A. Effect of saltation bombardment on the entrainment of dust by wind //Journal of Geophysical Research: Atmospheres. – 1993. – Т. 98. – №. D7. – С. 12719-12726.
- Chkhetiani O. G. et al. Dust resuspension under weak wind conditions: direct observations and model //Atmospheric Chemistry and Physics. – 2012. – Т. 12. – №. 11. – С. 5147.
- Malinovskaya E.A. Izv. Atmos. Oceanic Phys. 2019. 55(2). 86-92.
- Neuman C.M.K et al. Sediment. 2000. 47(1). 211-226.
- Semenov O.E. Introduction to experimental meteorology and climatology of the sand storms. Almaty. 2011. p 580 (in Russian).
Елена Александровна Малиновская
НИИ Механики МГУ
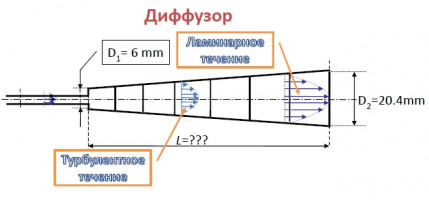
В работе исследовалось явление ламинарно-турбулентного пере-хода в диффузоре в зависимости от угла раскрытия и степени расшире-ния канала (отношения входного диаметра диффузора к выходному). При расчете использовалась трехпараметрическая модель сдвиговой турбулентности [1]. Расчеты проводились, при числах Рейнольдса на входе в канал от 100 до 4000. На вход в диффузор подавалось, либо развитое турбулентное течение, либо течение с равномерным профилем скорости и с разной энергией турбулентности. Угол раскрытия варьи-ровался от 0.01° до 4°, при этом течение в канале происходило, при по-ложительном, отрицательном или нулевом продольном градиенте дав-ления. Полученные при расчете характеристики течения на выходе диффузора и различных сечениях вдоль диффузора сравнивались с экс-периментальными данными [2]. При заданном угле раскрытия и степени расширения, течение в диффузоре зависит только от локального числа Рейнольдса и не зависит от условий на входе, пока эти условия доста-точны для формирования турбулентного течения. Было показано, что при увеличении длины диффузора турбулентное течение затухает и плавно переходит в ламинарное.
Получены зависимости критического числа Рейнольдса от угла раскрытия для диффузоров с разной степенью расширения 1.65, 2.5, 3.4 и 6.8 (обозначение индексов: 1 - вход в диффузор, 2 - выход из диффузора). При угле раскрытия 0.01°, что очень близко к прямой круг-лой трубе, критическое число Рейнольдса для заданных степеней рас-ширения лежит в диапазоне от ~900 до ~1000. Также получены зависи-мости рис. б критического числа Рейнольдса от угла раскрытия со сте-пенью расширения канала 3.4 и разной энергией турбулентности на входе в диффузор.
Владимир Викторович Трифонов
НИИ механики МГУ имени М.В. Ломоносова
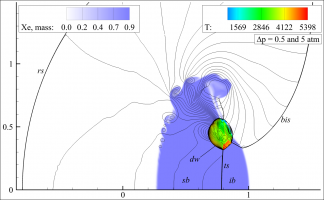
Описаны два подхода к моделированию течений горючих газовых смесей на основе уравнений Эйлера и конечно-объемного метода «MUSCLE» типа С.К. Годунова второго порядка аппроксимации, включающий HLLC-решатель локальных задач о распаде разрыва.
В первом подходе применяется модель равновесной смеси совершенных газов. Воздух моделируется смесью кислорода и азота в соотношении 1 к 4, а неоднородность заполнена пропано-кислородной смесью с добавлением азота и ксенона. Горение пропана моделируется одностадийной кинетикой Вестбрука.
Во втором подходе применяется модель совершенного газа с неоднородным распределением молярной массы. Реакция горения газовой смеси моделируется с помощью двухстадийной кинетики Коробейникова-Левина.
Описаны особенности реализации численного метода и кинетик горения, а также определена зависимость одномерной и двумерной структуры газовой детонации от параметров, входящих в модели горения.
Работа выполнена в НИИ механики МГУ имени М.В. Ломоносова с использованием ресурсов суперкомпьютерного комплекса МГУ имени М.В. Ломоносова при частичной финансовой поддержке Совета по грантам президента РФ (МК-3012.2019.1) и Российского фонда фундаментальных исследований (18-01-00793).
Олег Георгиевич Сутырин