НИИ механики МГУ
Вследствие вязкой диссипации в пограничном слое сверхзвукового потока сжимаемого газа происходит перераспределение температуры торможения. В результате температура торможения во внутренней части пограничного слоя – адиабатная температура стенки – оказывается ниже, а во внешней части – выше, чем температура торможения в основном потоке (для газов с числом Прандтля меньшем единицы). Определение адиабатной температуры стенки является одной из главных проблем при исследовании теплообмена сверхзвуковых потоков, поскольку ее непосредственное измерение в эксперименте затруднено. Для этого необходимо либо проведение длительных экспериментов на теплоизолированных моделях с достижением равновесного теплового режима, либо использование специальных методик математической обработки кратковременных экспериментов [1].
Внешние воздействия (градиент давления, проницаемость стенки, число Прандтля рабочего тела, форма и рельеф поверхности, скачки уплотнения и отрывные течения) могут приводить как к повышению аэродинамического нагрева в локализованной области, так и к охлаждению стенки. Известен эффект снижения адиабатной температуры стенки до значений ниже термодинамической температуры при поперечном обтекании дозвуковым сжимаемым потоком цилиндра в области задней критической точки (эффект Эккерта-Вайзе). За цилиндром (или, например, за выходной кромкой лопатки турбины) образуется вихревой след с температурной стратификацией по сечению вихря: в центре вихря полная температура ниже начальной, а на периферии – выше. Для сверхзвуковых потоков снижение адиабатной температуры стенки фиксируется в следе за обтекаемым препятствием в виде клина, ребра или ступеньки [2].
Данная работа направлена на исследование возможности снижения температуры по обводу профиля цилиндра, обтекаемого сверхзвуковым потоком сжимаемого газа. Экспериментальное исследование проводится на базе сверхзвуковой аэродинамической установки АР-2, на которой имеется возможность проведения бесконтактных исследований с помощью высокоскоростной ИК-камеры InfraTEC и иллюминатора из ZnSe (коэффициент пропускания 0.7), установленного на боковой стенке рабочей части установки.
1. Попович С.С. Особенности автоматизации эксперимента и обработки результатов при исследовании теплообмена в сверхзвуковом потоке сжимаемого газа // Программная инженерия. 2018. № 1. С. 35–45. DOI: 10.17587/prin.9.35-45
2. Leontiev A.I., Popovich S.S., Strongin M.M., Vinogradov Y.A. Adiabatic wall temperature and heat transfer coefficient influenced by separated supersonic flow // EPJ Web of Conf. 2017. V. 159. P. 1-5, DOI: 10.1051/epjconf/201715900030
Сергей Станиславович Попович
СтГАУ
Взаимодействие сред с различной динамикой движения рассматривается в рамках ветрового выноса частиц поверхности эолового происхождения.
Крупные частицы размерами от 30 до 300 мкм подскакивают над поверхностью до высоты около 20 см (сальтации), мелкие частицы микронного и субмикронного уровня поднимаются до высоты тысяч метров. Эти два различных типа движения связаны между собой [1]. Изменение концентраций микрочастиц связано с изменениями температуры поверхности и воздуха [2]. Поэтому необходимо изучение взаимодействий на микро-уровне в каналах пористой сыпучей среды.
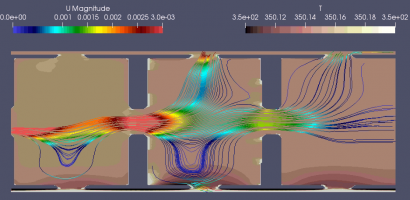
Для масштабов порядка долей и десятков микрометров проведение натурных экспериментов затруднено. В вычислительном эксперименте исследовалось влияние изменений температуры поверхности и скорости горизонтального потока над поверхностью на движение в пористой среде.
Область, повторяющая форму воздушного канала между частицами поверхности одного размера при прямоугольной укладке, построена с использованием моделирования 3D-объектов.
В качестве граничных условий при численном моделировании микропроцессов в воздушных каналах между частицами на поверхности приняты следующие: температура поверхности меняли от 310° до 350° К с шагом в 10°, скорость воздушного потока на верхней границе – от 0,01 до 0,05 м/с с шагом 0,01 м/с.
Вычислительный эксперимент реализован с использованием OPEN FOAM для ламинарной модели, учитывающей теплоперенос (рисунок). Величина составляющей скорости Uz восходящего потока в области взаимодействия модельной области канала с верхним потоком возрастает с увеличением температуры от 0,002 м/с до 0,0026 м/с, что определяет механизм микроконвекции у поверхности. В нижней области под слоем частиц составляющая скорости Uz отрицательна и скачком возрастает по модулю при температуре выше 330 К, что способствует отрыву от поверхности крупных сальтирующих частиц и выносу из пор частиц микронного и субмикронного размера.
Исследование выполнено при поддержке проекта РФФИ 19-05-50110.
1. Houser C. A., Nickling W. G. Sedimentology. 2001. 48(2). 255-267.
2. Chkhetiani O. G. et al. Atmospheric Chemistry and Physics. 2012. 12(11). 5147.
Денис Романович Малиновский
ИММ - обособленное структурное подразделение ФИЦ КазНЦ РАН
Серьезной проблемой загрязнения окружающей среды являются выбросы частиц аэрозоля микронного размера, связанные с дымовыми газами сжигания ископаемого топлива, химическим взаимодействием газов, измельчением твердых тел [1]. Для удаления частиц были разработаны различные технологии, такие как электрофильтры, высокоэффективные фильтры, обладающие низкой эффективностью. Ранее были проведены различные исследования резонансных режимов коагуляции и осаждения частиц [2, 3], доказавших свою эффективность в простых установках в виде трубы. Как известно, современные технические системы обладают компактностью и технологически сложностью конструкции. В связи с этим исследуются нелинейные колебания газа и аэрозоля в резонаторах различной формы и размеров.
Исследования ведутся в широком диапазоне частот и амплитуд возбуждения. Получена визуализация процесса осаждения аэрозоля в резонаторе при вынужденных колебаниях среды. Выявлены особенности изменения концентрации частиц от времени при различных начальных концентрациях. Дано сравнение для осаждения аэрозоля в трубе со скачком сечения от осаждения в гладкой трубе в безударно-волновом режиме колебаний.
Исследование выполнено при поддержке РФФИ № 19-01-00442 и гранта президента Российской Федерации (номер гранта МК-297.2020.1).
1. Медников Е. П. Акустическая коагуляция и осаждение аэрозолей. // М.: Изд-во АН СССР. 1963. 263 с.
2. Губайдуллин Д. А., Зарипов Р. Г., Ткаченко Л. А., Шайдуллин Л. Р. Экспериментальное исследование коагуляции и осаждения газовзвеси в закрытой трубе при переходе к ударно-волновому режиму // Теплофизика высоких температур. 2017. Т. 55. № 3. С. 484–486.
3. Губайдуллин Д. А., Зарипов Р. Г., Ткаченко Л. А., Шайдуллин Л. Р. Динамика табачного дыма при резонансных колебаниях в закрытой трубе // Теплофизика высоких температур. 2019. Т. 57. № 2. С. 312-315.
Линар Радикович Шайдуллин
ЦИАМ им. П.И. Баранова
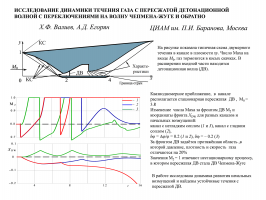
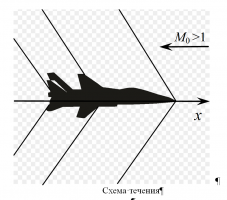
Изучается динамика течений идеального (невязкого и нетеплопроводного) газа с горением в структурно устойчивой детонационной волне (ДВ) – нормальной оси канала поверхности разрыва. Как установлено ранее [1], в такой постановке одномерные стационарные течения с горением в ДВ Чепмена - Жуге всегда неустойчивы, чего нельзя сказать о течениях с горением в пересжатой ДВ. Изучение динамики таких течений сведено к численному решению начально-краевой задачи, описывающей развитие конечных возмущений потока между движущейся ДВ и минимальным (при внезапном сужении) или выходным сечениями сопла [2]. Для ее решения модифицированной схемой Годунова повышенного порядка аппроксимации создан алгоритм расчета распада разрыва, допускающий переключения (с пересжатой ДВ на ДВ Чепмена - Жуге и обратно) явно выделяемых ДВ. Приведены примеры устойчивых и разрушающихся большими начальными возмущениями течений, с расчетом их динамики с вышеупомянутыми переключениями.
На рисунке показана типичная схема двумерного течения в канале в плоскости xy. Число Маха на входе M0, газ тормозится в косых скачках КС. В расширении входной части находится ДВ. Показаны характеристики Х-КИ течения газа в сопле и граница струи ГС.
Работа выполнена при поддержке РФФИ (20-01-00100 и 18-31-20059).
1.Крайко А.Н. Неустойчивость стационарных течений в каналах переменной площади поперечного сечения с детонационной волной Чепмена-Жуге // Прикл. матем. и механ. 2019. Т. 83. Вып. 3. С. 354-369.
2.Валиев Х.Ф., Крайко А.Н., Тилляева Н.И. Устойчивость одномерных стационарных течений с детонационной волной в канале переменной площади // Ж. выч. матем. и матем. физики 2020. Т. 60.№ 4. С. 711-724.
Харис Фаритович Валиев
НИИ механики МГУ им. М.В. Ломоносова
Изучение луночных углублений и их характеристик уже длительное время остается актуальной задачей современной механики и теплофизики. Подобные углубления являются хорошими интесификаторами теплообмена, не вызывающими, при этом существенного роста гидравлического сопротивления [1]. На практике этой свойство применяется при разработке теплообменных устройств макро- и микро-масштабов. Структура обтекания подобных углублений существенно зависит от относительной глубина (H/D). Так называемые «мелкие» лунки (H/D<0.25), характеризуются стационарным режимом обтекания, при котором в большинстве случаев, наблюдаются два симметричных вихря. При повышении отношения H/D до 0.25 стационарная структура потока в окрестности лунки разрушается и наблюдается формирование несимметричного течения с непериодическим чередованием «левостороннего» и «правостороннего» режима.
В настоящем исследовании проводится численное моделирование обтекания глубокой лунки (H/D=0.5) турбулентным потоком вязкой несжимаемой жидкости. Лунка располагается на нижней стенке плоскопараллельного канала, высотой 0.83 D. Входная и выходная границы канала расположены на расстоянии 4.5D, а расстояние от кромки лунки до боковых стенок канала составляет 1.5. Для описания турбулентного течения используется метод моделирования крупных вихрей (LES) c подсеточной моделью WALE [2]. Расчеты проведены для двух чисел Рейнольдса, вычисленных по диаметру лунки, ReD = 10 000 и ReD = 40 000. Для генерации турбулентности на входе использовался метод SEM (Synthetic Eddy Methods) [3].
Проведенные расчеты показали, что на наличие переключающихся режимов, кроме глубины лунки оказывает влияние и число Рейнольдса. Получено, что при ReD = 10 000 внутри лунки формируется практически симметричная вихревая структура, несимметричные переключающиеся структуры отсутствуют. Существенно иная картина формируется при увеличении числа Рейнольдса до 40 000. Наблюдается наличие переключающихся режимов, которые представляют собой одноядерные наклонные вихревые структуры, которые начинаются в одном конце лунки, пересекают продольную плоскость симметрии и выходят с противоположенного конца. Осреднение по трем циклам дает в среднем близкую к симметричной картину, которая при этом отличается от полученной для ReD = 10 000. Кроме того, было проведено осреднение за период существования одного режима, в этом случае получается характерная одноядерная вихревая структура.
Работа выполнена при финансовой поддержке РФФИ (грант № 19-01-00242).
1.Дзюбенко Б.В., Кузма-Кичта Ю.А., Леонтьев А.И., Федик И.И., Холпанов Л.П. Интенсификация тепло- и массообмена на макро-, микро- и наномасштабах. - М.: ФГУП “ЦНИИАТОМИНФОРМ”, 2008, с цв.вкладкой
2.Nicoud, F. and Ducros, F., 1999. “Subgrid-Scale Stress Modelling Based on the Square of the Velocity Gradient Tensor,” Flow, Turbulence and Combustion, 62, pp. 183-200.
3.Jarrin, N., Benamadouche, S., Laurence, D., and Prosser, R. 2006. “A synthetic-eddy-method for generating inflow conditions for large eddy simulations”. International Journal of Heat and Fluid Flow, 27, pp. 585-593
Алексей Юрьевич Чулюнин
МГУ имени М.В. Ломоносова
В биологических приложениях при течении жидкостей в моделях кровеносных сосудов возникают различные явления, которые оказывают влияние на характер течения и на деформацию стенок, что влечёт за собой дисфункциональные изменения в организме человека или животного.
Ранее в литературе исследовались, в основном, течения ньютоновской (линейно-вязкой) или идеальной жидкости [1, 2]. Хотя, кровь в средних и мелких сосудах обладает неньютоновскими свойствами. При этом одномерное моделирование течения крови по кровеносным сосудам является удобным инструментом для изучения динамики биологической жидкости в системе кровообращения.
Данное исследование проводилось классическими методами теории устойчивости, на основе ранее разработанной одномерной модели [3, 4]. Для трубок бесконечной длины рассматривались решения в виде бегущих волн и выводилось дисперсионное уравнение. Анализом его корней находились области неустойчивости в пространстве параметров.
Поскольку критерий устойчивости для сколь угодно большой длины трубки не совпадает с критерием устойчивости для бесконечно длинной трубки, то для определения границ устойчивости задача была исследована на нахождение области глобальной неустойчивости. В данном случае использовался асимптотический метод глобальной неустойчивости, разработанный А.Г. Куликовским [5].
Кроме того, для трубок конечной длины была решена задача на собственные значения. Граница устойчивости исследовалась численно с учетом упругости стенки трубы, продольного натяжения и длины трубки.
1.Grotberg J.B., Jensen O.E. Biofluid mechanics in flexible tubes // Ann. Rev. Fluid Mech. 2004. Vol.36. P.121–147.
2. Heil M., Hazel A.L. Fluid-Structure Interaction in Internal Physiological Flows // Ann. Rev. Fluid Mech. 2011. Vol.43. P.141–162.
3. Порошина А.Б., Веденеев В.В. Существование и единственность стационарного состояния упругой трубки при протекании через нее степенной жидкости // Российский журнал биомеханики. 2018. Т. 22. № 2. С. 196–222.
4. Веденеев В.В., Порошина А.Б. Устойчивость упругой трубки, содержащей текущую неньютоновскую жидкость и имеющей локально ослабленный участок // Труды МИАН. 2018.
Т. 300. С. 42–64.
5. Куликовский А.Г. Об устойчивости однородных состояний // Известия АН СССР. ПММ. 1966. Т. 30. Вып. 1. С. 148-153.
Анастасия Борисовна Подопросветова
Институт теплофизики им. С. С. Кутателадзе СО РАН
Моделирование режимов работы вихревых реакторов необходимо для интенсификации тепло- и массопереноса. Особое внимание при исследовании ограниченных вихревых течений уделяется изучению распада вихря из-за важных приложений в химических, биологических и энергетических технологиях. Изучение природы распада вихря часто проводится в цилиндрическом контейнере, из-за канонической формы геометрии и малого количества определяющих параметров. Сравнительно недавно внимание исследователей привлекли двух-жидкостные вращающиеся течения в связи с развитием вихревых биореакторов. Для повышения эффективности работы вихревых устройств, таких как вихревые биореакторы, необходимо комплексное исследование структуры вихревых течений и процессов массопереноса.
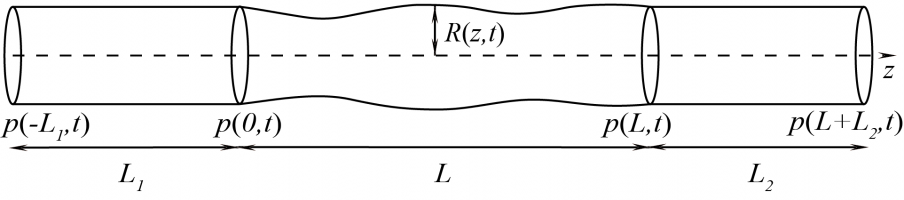
В работе было проведено экспериментальное исследование структуры вихревого течения двух несмешиваемых жидкостей в замкнутом цилиндрическом контейнере. В работе показано, что распад вихря в зависимости от свойств и объемов жидкостей может происходить (а) в верхней [1], (б) в нижней [2] или (в) в обеих жидкостях одновременно. Опыты проводились в цилиндрическом контейнере с радиусом R = 45 мм и высотой h = 2,5R с верхним торцом, вращающимся с угловой скоростью ω. В качестве верхней жидкости использовалось подсолнечное масло (rо = 920 кг/м3, nо = 49 мм2/с), нижней - водный раствор глицерина. Толщина слоя верхней жидкости ho = 1R, а нижней hg = 1.5R. Скорость вращения характеризуется числом Рейнольдса Re = ωR2/νо. Для изучения структуры потока применялся метод цифровой трассерной визуализации.
На рисунке 1(а) показан пример распада вихря, наблюдаемый в верхней жидкости при Re = 800, в то время как в нижней жидкости (водный раствор глицерина с ρg = 1208 кг/м3 и νg = 43 мм2/с) распада вихря не происходит. На рисунке 1(б) показан распад вихря в нижней жидкости (дистиллированная вода) при Re = 300. На рисунке 1(в) показан распад вихря в верхней и в нижней жидкости (водный раствор глицерина с ρg = 1070 кг/м3 и νg = 3 мм2/с) при Re = 700. Таким образом, двух-жидкостный вихревой поток можно эффективно контролировать, выбирая соответствующие объемы и свойства жидкостей.
Работа выполнена при поддержке гранта РФФИ № 18-08-00508.
Список литературы:
1. Naumov I.V., Glavny V.G., Sharifullin B.R., Shtern V.N. Formation of a thin circulation layer in a two-fluid rotating flow // Phys. Rev. Fluids, 2019, vol. 4, 054702.
2. Naumov I.V., Sharifullin B.R., Shtern V.N. Vortex breakdown in the lower fluid of two-fluid swirling flow // Phys. Fluids, 2020, vol. 32, 014101.
Булат Руфкатович Шарифуллин
Московский государственный университет имени М.В.Ломоносова
Потоки на склонах, такие как снежные лавины, грязекаменные сели, оползни, подводные мутьевые потоки, в процессе движения разрушают подстилающую поверхность и уносят массу вниз по течению. В случае селевых или подводных мутьевых потоков интерес представляет глубина разрушения склона, так как потоком могут быть разрушены элементы инфраструктуры, изменена форма русла. В случае снежных лавин разрушение подстилающей поверхности изучается для определения изменения массы потока, так как в процессе движения масса потока может измениться в несколько раз, это важно учитывать при проектировании заградительных сооружений.
Для моделирования разрушения потоком и вовлечения в движение материала склона используется многофазный подход. Методом контрольных объёмов рассчитывается движение 3 фаз: материал подстилающей поверхности, материал движущегося потока, воздух. Используется решатель multiphaseInterFoam пакета OpenFOAM. В качестве механизма захвата рассматривается захват при превышении напряжения на дне потока некоторого порогового значения, описанный в работах [1, 2]. Материал потока представлен средой Хершеля-Балкли, использование данного реологического закона позволяет смоделировать процесс отложения материала потока на поверхности склона, а также остановку потока.
Для верификации полученной модели течения рассчитывается снежная лавина в 22 очаге на горе Юкспор (Хибины). Последний раз катастрофическая лавина сошла здесь в 2017 году, тогда были засыпаны автомобильная и железная дороги, выбиты окна в близлежащем доме, погибли 3 человека. В работе используются данные о лавине из этого очага, сошедшей в 1965 году. Для этой лавины известна масса сорвавшегося снега и масса лавинных отложений, что позволяет оценить количество захваченного потоком материала.
Дарья Игоревна Романова
Пермский государственный национальный исследовательский университет
В работе [1] проведено численное исследование ламинарной нестационарной естественной конвекции в замкнутой кубической полости, имеющей локальный источник тепла различной геометрической формы. Для такой системы с цилиндрическим компактным нагревателем предложена численная модель, которая предсказывает возникновение двух противовращающихся тороидальных вихрей.
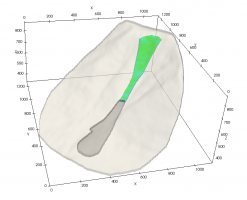
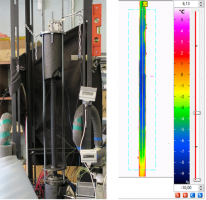
Для подтверждения наличия такой особенности был поставлен эксперимент, схема которого представлена на рис. 1. Кювета 2 представляет собой стеклянный параллелепипед высотой 25 см с квадратным основанием со стороной 19 см. В центре нижнего основания кюветы расположен медный кубический нагреватель со стороной 2.4 см. В качестве рабочей жидкости выступает вода при нормальных условиях. Для регулирования температуры используется электрический нагреватель на основе PID регулятора 4.
В ходе эксперимента с помощью лазера 1 и цилиндрической линзы был получен лазерный нож, вырезающий исследуемую область в центре кюветы. С использованием камеры 5 и флуоресцентного красителя изучалась структура установившегося конвективного течения. Для получения поля скорости жидкости в центральном сечении кюветы, использовались полиамидные светоотражающие частицы и метод PIV.
1.Gibanov N. S., Sheremet M. A. Natural convection in a cubical cavity with different heat source configurations //Thermal Science and Engineering Progress. – 2018. – Т. 7. – С. 138-145.
Матвей Максимович Гончаров
НИИ механики МГУ им. М.В. Ломоносова
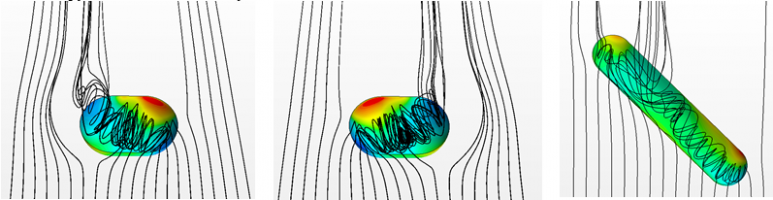
Исследование механизмов обтекания лунок различной глубины, является актуальной задачей современной механики. Известно, что подобные углубления являются хорошими интенсификаторами теплообмена и не вызывают при этом сильного роста коэффициента гидравлического сопротивления. В зависимости от отношения максимальной глубины H и диаметра пятна D принято различать мелкие (H/D<0.125), умеренные (0.125 <Δ< 0.25) и глубокие (H/D>0.25) лунки [1]. В мелких лунках течение безотрывное, а в умеренных – возникают характерные вихревые структуры в виде симметричной двухъячеистой области рециркуляционного течения. В глубоких лунках стационарные схемы течения оказываются неустойчивыми, наблюдается формирование нестационарного течения с непериодическим чередованием «левостороннего» и «правостороннего» несимметричных режимов. Последние работы (например, [2]) показывают, что эффективная форма вихрегенератора – овально-траншейная лунка (ОТЛ).
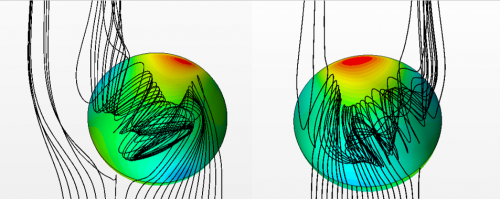
В работе на базе численного моделирования исследуется структура течения в глубоких овально-траншейных лунках, расположенных различными углами к набегающему потоку, на нижней стенке плоскопараллельного канала. Траншея представляет собой две половинки полусферической лунки радиуса R, соединенных между собой полуцилиндрической вставкой, длина которой L варьируется в широком диапазоне. Для дискретизации расчетной области применялась неструктурированная сетка размером до 15 млн. элементов. Число Рейнольдса вычисленное по скорости потока на входе в канал и диаметру начального пятна лунки изменяется в диапазоне от 104 до 105.
В ходе проведения вычислительного эксперимента выявлено, что увеличение длины цилиндрической части лунки от 0 до L=R приводит к стабилизации течения, воспроизводятся два устойчивых стационарных состояния, характеризуемые одноядерными вихревыми структурами, начинающимися на внутренних стенках концевых сферических скруглений траншеи и выходящих во внешнюю пристеночную область течения в районе противоположных концов траншеи (Рис.1а, б). Конкретная конфигурация зависит от предыстории установления, в частности – от начальных условий задачи. Дальнейшее увеличение длины лунки, а также поворот лунки относительно набегающего потока устраняет неоднозначность решения и приводит к новым, более сложным вихревым структурам (Рис.1в).
Алексей Юрьевич Чулюнин
НИИ механики МГУ
В технике известен способ безмашинного энергоразделения газового потока. В основе данного способа лежит тепловое взаимодействие между сверхзвуковым и дозвуковым потоками, разделенными теплопроводной перегородкой. Сжатый газ разделяется на 2 потока: дозвуковой, текущий, например, по центральному каналу, и сверхзвуковой – по кольцевому [1]. Часть газа, поступающая в сверхзвуковое сопло, теряет полное давление при разгоне и торможении в диффузоре и подогревается за счет теплообмена через стенку с дозвуковым потоком.
С помощью устройства энергоразделения можно компенсировать снижение температуры газа при дросселировании. Ранее было показано, что дроссель-эффект при работе устройства энергоразделения на воздухе полностью перекрывается нагревом сверхзвукового потока от дозвукового [2]. Актуальным представляется возможность применения устройства энергоразделения для подогрева природного газа при редуцировании его давления на газораспределительных станциях.
В рамках данной работы проводится исследование устройства энергоразделения на гидратообразующем компоненте природного газа – углекислом газе. На первом этапе с помощью ИК-камеры InfraTEC проведено измерение адиабатной температуры стенки при течении в канале сверхзвукового потока углекислого газа, а также серия экспериментальных измерений распределения статического давления по длине канала при работе на воздухе и углекислом газе.
1. Leontiev A.I., Popovich S.S., Vinogradov U.A., Strongin M.M. Experimental research of supersonic aerodynamic cooling effect and its application for higher energy separation efficiency // International Heat Transfer Conference. Proceedings of the 16th International Heat Transfer Conference, IHTC 2018. P. 2987-2994.
2.Попович С.С., Киселёв Н.А., Макарова М.С. Использование сверхзвукового безмашинного энергоразделения для подогрева газа при дросселировании // Одиннадцатая Всероссийская конференция молодых ученых и специалистов «Будущее машиностроения России»: сборник докладов. Издательство МГТУ им. Н. Э. Баумана, 2018. С. 443–446.
Сергей Станиславович Попович
Научно-исследовательский московский комплекс «Центральный аэрогидродинамический институт им. проф. Н.Е. Жуковского»
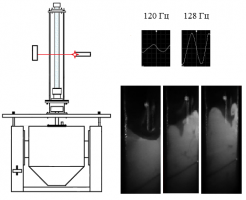
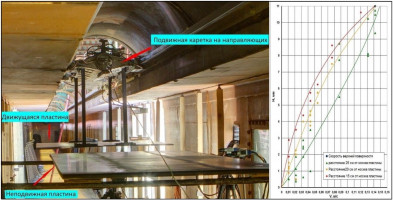
В целях верификации визуализационно-видеографической системы (ВВИС) [1], реализованной в виде макета мобильной измерительной системы (МИС) проведена серия экспериментов на установке прямого движения ‑ скоростном гидростенде ЦАГИ (ГСС, г. Дубна. Исследовалось движение тонкой плоской пластины (ТПП) размером 1470х1000х10 мм, установленной на подвижной каретке, с различными скоростями V=3÷6 м/с в режиме штатного движения и с малой скоростью V=0.15 м/с в режиме возвратного хода каретки. Движение осуществлялось в присутствии неподвижного плоского экрана размером 2400х900х20 мм, располагаемого на различных высотах h под движущейся пластиной в диапазоне h=0.01÷ 0.1 м. Система крепления экрана внутри канала ГСС позволяла изменять h непрерывно.
Поле скорости в щели между ТПП и экраном измерялось по авторской методике ВВИС. Результаты измерения профилей продольной скорости в щели для различных расстояний от передней кромки ТПП сравнивались с точными классическими аналитическими решениями разгонного течения Куэтта в рамках пространственно-временной связи x=Vt. Степень количественного совпадения этих результатов позволяет признать верификационную процедуру состоявшейся. Ниже на рисунке приведены графики профилей разгонного течения Куэтта, полученные по результатам обработки экспериментальных данных для h=0.01 м и V=0.15 м/с.
Другая серия экспериментов была выполнена по такой же схеме с моделью телесной пластины (толщина 0.05 м) с оживальным скруглением передней и задней кромок. Одним из непредсказуемым априори результатов оказалось существование в зазоре между движущейся пластиной и неподвижным экраном области, где в связанной с экраном системе отсчёта скорость потока направлена навстречу движущейся пластине. Первоначально было решено, что такое явление связанно с несовершенством экспериментальной установки. Но проведённое впоследствии численное математическое моделирование схематизированного эксперимента показало, что физическое явление существует и результаты эксперимента можно считать достоверными.
1. Айрапетов А.Б., Катунин А.В., Стрекалов В.В. Измерение скоростей потока за плохообтекаемым телом визуализационно-видеографическим методом// Тезисы XXVI научно-технической конференции по аэродинамике. 2015 г.
Андрей Владимирович Катунин
ЦИАМ им. П.И. Баранова
Огромное многообразие работ по математическому моделированию звукового удара, возникающего при полёте сверхзвуковых гражданских самолетов, предполагает разбиение всего течения на две подобласти: близкую к летательному аппарату (ЛА) и далекую от него. В близкой подобласти возмущения течения велики, а скачки уплотнения (ударные волны - УВ) интенсивны и имеют сложную пространственную структуру. В системе координат ЛА течение в этой подобласти в основном стационарное и сверхзвуковое с небольшими дозвуковыми зонами, в частности, вблизи затупленных кромок крыльев. Влияние нестационарности вихрей, сходящих с концов крыльев и хвостового оперения, реактивных струй и турбулентности в пограничных слоях на эволюцию ударно-волновых структур, ответственных за звуковой удар, невелико и убывает с удалением от ЛА. Поэтому для моделирования звукового удара расчет течения в ближней подобласти возможен в рамках уравнений Эйлера. По сравнению с современными расчетами обтекания всего ЛА в приближении осредненных по Рейнольдсу уравнениями Навье-Стокса (RANS) такой расчет много проще, ибо не требует сгущения сетки у поверхностей, обтекаемых без прилипания, и пограничных слоев. Существенно то, что установлением по времени нужно рассчитывать область, ограниченную длиной ЛА, а далее вести счет маршем по оси х, направленной по скорости набегающего на ЛА сверхзвукового потока. Чтобы правильно рассчитать эволюцию ударно-волновой структуры, при маршевом счете следует при каждом х ограничиваться только возмущенной областью, по возможности адаптируя сетку к зоне УВ. При удалении по х от ЛА на 5-10 его длин, когда максимальное относительное возмущение давления |Dp/p0| уменьшится до 0.1, следует переходить к маршевому счету [1] в приближении нелинейной акустики. Явное выделение в этом приближении "внешней" и "внутренней" близких к коническим, "бегущих в одном направлении" слабых УВ при на порядки меньшем, чем вблизи ЛА общем фиксированном числе ячеек позволит рассчитать звуковой удар на расстояния в многие сотни длин ЛА. Ключевой элемент такого расчета - одно семейство сеточных линий, "бегущих в том же направлении" и как следствие - адаптированных к волновой "квазикольцевой" (в дальней подобласти) структуре звукового удара.
Работа выполнена при поддержке РФФИ (20-01-00100 и 18-31-20059).
1.Годунов С.К., Забродин А.В., Иванов М.Я. и др. Численное решение многомерных задач газовой динамики. М.: Наука, 1976. 400 с.
Харис Фаритович Валиев
ИПФ РАН
Морской аэрозоль в приповерхностном слое играет огромную роль в процессах обмена импульсом, теплом и газообмена. В настоящий момент мелкомасштабные быстропротекающие процессы обуславливающие механизмы образования брызг при ветро-волновом взаимодействии изучены слабо. В натурных условиях это сделать практически невозможно, поэтому прибегают к моделированию на крупномасштабных ветро-волновых каналах. При этом наиболее перспективными методом регистрации событий представляется высокоскоростная видеосъемка со специальной визуализацией.
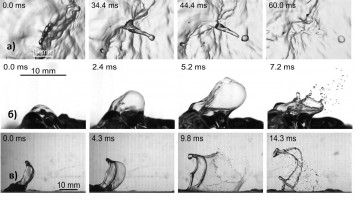
В настоящей работе приведены исследования, выполненные на Ветро-Волновом Термостратифицированном бассейне (ВВТСБ) ИПФ РАН [1]. С помощью высокоскоростной видеосъемки и теневой подсветки были получены изображения, характеризующие процессы образования брызг. Теневые фотографии типичных событий, приводящих к генерации капель, показаны на Рис. 1 (а-в). Мможно предложить их следующую классификацию:
1. Дробление жидких "пальцев" (Рис. 1а). В районе гребней обрушающихся волн развиваются небольшие выступы воды, которые затем растягиваются в «пальцы» и разрываются на одну-две капли диаметрами несколько миллиметров.
2. Разрыв подводных пузырей (Рис. 1б). Подводные пузыри, формирующиеся у гребней обрушающихся волн, всплывают из-за положительной плавучести и разрываются при достижении поверхности воды, генерируя брызги.
3. Дробление типа "парашют" (Рис. 1в). Это явление начинается с появления мелкомасштабного возвышения водной поверхности, затем развивающегося в «микро-парус», который раздувается разрывается, образуя сотни брызг.

Рис. 1. Фотографии событий, сопровождающих генерацию брызг: а) дробление жидких "пальцев" (вид сверху); б) разрыв подводных пузырей (вид сбоку); в) нижний ряд фотографий – формирование и разрыв «парашюта» (вид сбоку)
Максим Игоревич Вдовин
НИИ механики МГУ
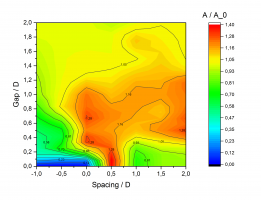
Усиление амплитуды колебаний цилиндра у задней кромки пластины по сравнению с амплитудой одиночного цилиндра. Gap – зазор между поверхностями цилиндра и пластины, Spacing – смещение центра цилиндра по потоку относительно задней кромки пластины. Направление потока – слева направо, поверхность пластины соответствует Gap=0.
Колебания, возникающие в поперечном потоке жидкости или газа за плохо обтекаемыми телами из-за периодического срыва вихрей могут приводить к неприятным условиям эксплуатации различных конструкций, вплоть до их разрушения, но в то же время эти резонансные колебания можно использовать в малых устройствах, преобразующих энергию движения среды в электроэнергию, поэтому изучение этого явления имеет большую практическую значимость.
В данном исследовании рассматривается обтекание упругого цилиндра – резинового круглого шнура диаметром D = 6 мм, установленного в рабочей части аэродинамической трубы с поперечным сечением 500x300 мм. Скорости, на которых наблюдаются резонансные колебания, соответствуют 0.4-0.6 м/с.
В предварительных экспериментах с одиночным цилиндром получена максимальная относительная амплитуда колебаний A/D ~ 0.29 и качественное сходство с другими экспериментами [1], проведенными преимущественно на упруго подвешенных цилиндрах. Визуализация показала небольшую модификацию вихревой дорожки из-за осцилляции шнура. Следующие серии экспериментов проводились при поперечном относительно скорости потока расположении упругого шнура и: а) жесткого цилиндра такого же диаметра; б) жесткой пластины, сонаправленной с потоком. Влияние зазора G между упругим шнуром и вторым объектом на амплитуду показано на рисунке. Для тандема цилиндров найдено, что при зазоре, меньшем половины, колебания отсутствуют, а для 1–1.5 диаметров существует плато, где амплитуда колебаний приблизительно одинакова, затем оно резко переходит в зону отсутствия взаимного влияния цилиндров друг на друга.
В случае расположения цилиндра рядом с пластиной последняя имела длину 35 мм, толщину 2 мм, а концы скруглены по эллипсу с полуосями 3 и 1 мм. Было найдено, что амплитуда колебаний уменьшается при расположении цилиндра «над» пластиной (Рис., S < 0). В непосредственной близости от задней кромки цилиндра и далее по потоку (S > 0) обнаружены зоны усиления колебаний амплитуды вплоть до 40% по сравнению с одиночным цилиндром. На дымовых визуализациях видно, что присутствие цилиндра у задней кромки пластины приводит к более скорому развитию неустойчивости следа пластины, который разрушается в вихри, напоминающие вихри Кельвина-Гельмгольца. Скорее всего, присутствие этих вихрей, сходящих с частотой парных вихрей кармановского типа, воздействуют на цилиндр в фазе движения и усиливая колебания.
1. Williamson C. H. K., Govardhan R. Vortex-induced vibrations //Annu. Rev. Fluid Mech. 2004. Т. 36. С. 413-455.
Олег Олегович Иванов