Пермский национальный исследовательский политехнический университет
Неправильное функционирование и физиология трехстворчатого аортального клапана оказывает негативное влияние на системный кровоток в организме человека. Причины нарушения работы клапана могут быть разными: стеноз или неправильное развитие системы кровообращения на эмбриональном этапе, и т.д.
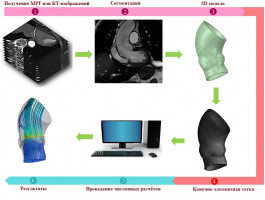
В представленной работе было проведено исследование по зависимости гемодинамики в аортальном клапане в зависимости от формы створок и их биомеханических свойств. Используя результаты мультиспиральной компьютерной томографии был получен набор геометрии клапанов реальных пациентов. Далее была построена компьютерная модель кровотока в исследуемом участке с учетом двустороннего взаимодействия жидкости и твердого тела [1]. Были получены распределения скоростей, давлений, НДС створок. Исследовалось влияние изменения толщины створок клапана и их биомеханических свойств материала. Результаты работы сравнивались с результатами, полученными в работе [2]. Показано хорошее качественное и количественное совпадение результатов. В дальнейшем планируется сравнительный анализ течения крови в аортальном клапане в норме, при патологии и после хирургического вмешательства для анализа его последствий.
1.Kochergin, M. Investigation of fluid flow in the curved tube at 1-way and 2-way fluid-structure interaction // Mater’s Journal. 2020. Vol. 1. P. 228–239.
2.Gilmanov A., Barker A., Stolarski H., Sotiropoulos F. Image-guided fluid-structure interaction simulation of transvalvular hemodynamics: quantifying the effects of varying aortic valve leaflet thickness // Fluids. 2019. Vol. 4, 119. https://doi.org/10.3390/fluids4030119
Максим Владимирович Кочергин
Пермский Национальный Исследовательский Политехнический Университет
Некоторые кости скелета человека внутри имеют пористую структуру, напоминающую губку. Отсюда и название такого типа костной ткани – губчатая. В 19 веке ученые обратили внимание, что структурные единицы губчатого вещества располагаются вдоль преобладающей нагрузки, действующей на костную ткань [1], что делает ее прочнее в данном направлении. Дальнейшие наблюдения показали, что в течение жизни структура губчатой ткани может меняться в зависимости от внешней нагрузки. Способность кости приспосабливать внутреннюю структуру к внешним воздействиям привлекла многих врачей и учеными своими широкими возможностями. Исправление прикуса посредством брекетов – один из ярких примеров использования адаптационных свойств кости на благо человечества.
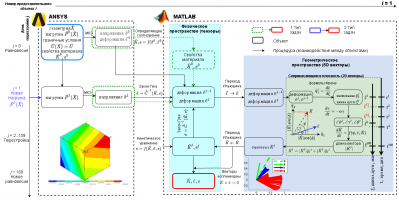
В данной работе представлена модель адаптации кости, в основе которой лежит гипотеза о том, что структурные единицы костной ткани в процессе адаптации выстраиваются вдоль линий действия наибольших механических нагрузок. Для описания изменения структуры используется система кинетических уравнений, согласованных с обобщенным законом Гука, в котором свойства материала рассчитываются на основе тензора структуры [2,3,4]. Расчёт ведется в программных продуктах ANSYS и MATLAB по схеме, изброженной ниже:
При помощи данной модели возможно предсказать результат врачебного вмешательства для каждого пациента в каждом конкретном случае и при необходимости, скорректировать силу и направление воздействия на костную ткань.
Работа выполнена при финансовой поддержке Правительства Пермского края.
1. Wolff J. Das Gesetz der Transformation der Knochen. Berlin: Hirshwald, 1892. 416 p.
2. Зубчанинов В.Г. Основы теории упругости и пластичности. М.: Высш. шк. 1990. 368 с.
3. Чикова Т.Н и др. Моделирование перестройки трабекулярной костной ткани в ветви нижней челюсти человека // Российский журнал биомеханики. 2018. Т. 22. № 3. С. 292–300.
4. Тверье В.М. Кинетические уравнения перестройки трабекулрной костной ткани в пространстве Ильюшина. // Российский журнал биомеханики. 2019. Т.23. № 2. С. 293-301.
Татьяна Николаевна Чикова
МИРЭА – Российский технологический университет

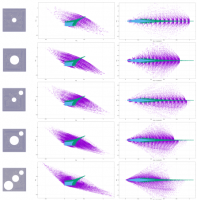
Пространственное распространение пандемии COVID-19 изучается с помощью кинетического метода с введением двух параметров. Предлагается одномерная модель на основе уравнения кинетического типа для изучения динамической плотности распределения носителей вируса во времени и пространстве с учетом их миграции из выделенного центра. Данная модель является новой и принципиально отличается от известных моделей типа диффузия-реакции. Строится аналитическое решение; для получения серии расчетов применяются и численные методы. Производится сравнение модельных и реальных данных в Италии, России и Чили (возможность применения простой одномерной модели для этих стран связана с особенностями их географического положения). Помимо скорости заражения, вводится в рассмотрение «скорость выздоровления». При прохождении волны выздоровления по территории с большей частью населения страны делается вывод о начале глобального выздоровления, что соответствует реальным данным. Предсказания оказываются точными и для второй волны пандемии в России. Ожидается, что модель способна адекватно описать не только развитие COVID-19, но и последующих эпидемий.
Андрей Дмитриевич Ястребов
Донской Государственный Технический Университет
Одна из основных задач офтальмологии на сегодняшний день является исследование механических характеристик тканей глаза, знание которых позволяет предвидеть группу заболеваний, связанных непосредственно с дегенеративными заболеваниями глаза, в первую очередь к таким заболеваниям относятся кератоконус и дистрофия, которые в отсутствии терапии приводят к ухудшению и потере зрения. Так же при получении данных характеристик, появляется возможность уменьшить риски во время проведения межслойной рефракционной кератопластики – пересадки части роговицы донора между слоями роговицы пациента – требует предварительного исследования напряженно-деформированного состояния роговицы под действием внутриглазного давления. В этом случае можно построить оболочечную расчетную схему с использованием нескольких базовых поверхностей. В основе модели лежит кинематическая гипотеза, по которой пространственное поле деформации оболочки определяется деформацией нескольких базовых поверхностей, а также операций по восстановлению отдельных тканей роговицы.
Изучение механических характеристик тканей глаза, так же важно для разработки новых биосовместимых материалов, используемых для создания новых видов имплантов, а также возможности прогнозирования осложнений, что позволяет выбрать метод операции.
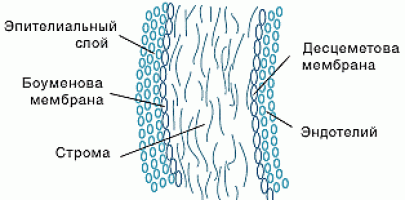
В настоящей работе предложен метод исследования механических характеристик, путем рассмотрения топологических особенностей слоев роговицы глаза, а также соседних тканей. Данная методика учитывает особенности клеточного строения мягких тканей глаза, а также предполагает возможность рассмотрения клеточного строения отдельных слоев, таких как: передний эпителий, передняя пограничная мембрана (Боуменова), строма, слой Дюа, задняя пограничная оболочка (Десцеметова оболочка), задний эпителий.
В качестве образцов, для отработки методики, использовались энуклеированные глазные яблоки кроликов, предоставленные Ростовским государственным медицинским университетом (РостГМУ). Исследования проводились с разрешения этического комитета РостГМУ. Топология поверхности роговицы была получена с помощью атомно-силового сканирующего микроскопа NanoEducator (NT-MDT, Россия). Наведение проводилось при помощи позиционирующей микроскопии. Для сканирования использовались зонды с вольфрамовым наконечником, заточенные электро-химическим способом. Для обработки полученных результатов, использовалась программная среда Gwyddion.
Роман Витальевич Кароткиян
Научно-исследовательский институт механики МГУ имени М.В. Ломоносова
В настоящее время предпринимаются многочисленные попытки применения моделей сердечной мышцы, миокарда, для исследования условий зарождения и длительного существования аритмий в стенках камер сердца, а также для выработки рекомендаций по их лечению. Имеются опытные данные о зависимости скорости распространения волны возбуждения в миокарде от его деформации. Однако большинство моделей мышцы не только не учитывают эту механо-электрическую обратную связь, но и, зачастую, не содержат какого-либо описания активной механики миокарда. Представленные в литературе модели миокарда не показывают важные зависимости развиваемой мышцей силы от частоты стимуляции, и моделируемое ими распространение волн электрического возбуждения представляется нам недостаточно адекватным.
В докладе предложена новая модель электромеханики сердечной мышцы, включающая описание цепочки процессов, ведущих от электрической активации мышцы к её механическому сокращению, и влияния напряжённо-деформированного состояния мышцы на характеристики волны электрической активации. Механический блок представлен разработанной нами ранее моделью [1], учитывающей процессы взаимодействия сократительных и регуляторных белков мышцы и воспроизводящей большой набор опытных данных. Электрофизиологический блок представлен простой феноменологической моделью [2], которая хорошо воспроизводит вид разности потенциала на мембране и его изменение с частотой стимуляции. Для электромеханического сопряжения использовали модель [3], которую упростили и модифицировали. Эта модель учитывает важный механизм кальций-инициируемого высвобождения кальция в клетку.
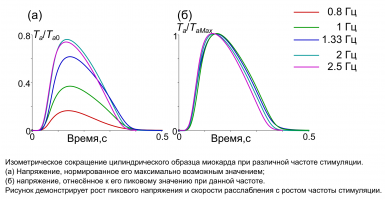
Решена задача о сокращении цилиндрического образца сердечной мышцы в различных режимах деформации и нагружения. Полученные результаты демонстрируют согласованные с опытными данными зависимости силы и внутриклеточной концентрации ионов кальция от частоты стимуляции или длительности одиночной паузы после периодического сокращения. Модель воспроизводит важные медленные эффекты, связанные с изменением длины мышцы или частоты стимуляции.
Работа поддержана грантом РНФ № 20-74-00046.
-
Syomin FA, Tsaturyan AK. A simple model of cardiac muscle for multiscale simulation: Passive mechanics, crossbridge kinetics and calcium regulation // J Theor Biol. 2017. V. 420. P. 105-116.
-
Aliev RR, Panfilov AV, A simple two-variable model of cardiac excitation // Chaos, Solitons & Fractals. 1996. V. 7(3). P. 293-301.
-
ten Tusscher KH, Panfilov AV. Alternans and spiral breakup in a human ventricular tissue model // Am J Physiol Heart Circ Physiol. 2006. V. 291(3). P. H1088-H1100.
Фёдор Александрович Сёмин
Институт Гидродинамики им. М.А. Лаврентьева СО РАН
Церебральная артериовенозная мальформация (АВМ) является патологией развития сосудов головного мозга, при которой артериальное и венозное кровеносные русла соединены клубком беспорядочно переплетенных вырожденных сосудов. Наиболее предпочтительным методом лечения данных патологий является эмболизация - внутрисосудистое заполнение клубка патологических сосудов АВМ специальным эмболическим агентом (например, ONYX) с целью блокирования кровотока через них. Данный способ хирургического вмешательства широко применяется, но до сих пор в некоторых случаях сопровождается периоперационным разрывом сосудов мальформации. В работе математически моделируется процесс эмболизации и строится алгоритм, позволяющий находить её оптимальные режимы.
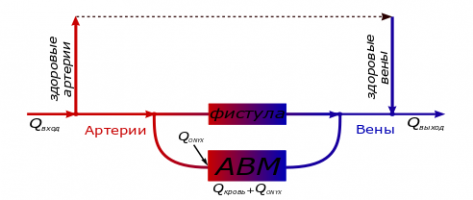
Для описания процесса эмболизации предлагается модель, в которой наряду с течением крови и эмболического агента в мелкососудистой части АВМ и фистуле (крупном выделенном сосуде патологии) учитывается перераспределение крови в окружающие здоровые сосуды. Процесс эмболизации АВМ моделируется как процесс двухфазной фильтрации несмешивающихся несжимаемых жидкостей, где вытесняемой фазой является кровь, а вытесняющей эмболический агент, получаемая система уравнений решается численно с помощью монотонной модификации схемы CABARET [1]. Во время эмболизации поток крови, поступающий в АВМ, меняется за счет перераспределения в соседние здоровые сосуды из-за увеличивающегося во время операции сопротивления патологии, в модели этот эффект учитывается путем введения дополнительных соотношений.
Основная цель работы заключается в отыскании оптимального с точки зрения безопасности и эффективности сценария эмболизации. Целевой функционал и ограничения, возникающие в такой задаче оптимального управления, выбираются в соответствии с медицинскими показаниями, а управлением является объёмный расход эмболического агента на входе в АВМ. Сформулирована и для специального закона подачи эмболического агента численно решена задача оптимального управления многоэтапной эмболизацией. При решении задачи использовались клинические данные, полученные во время мониторинга гемодинамических параметров во время нейрохирургических операций в НМИЦ им. Мешалкина [2].
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 20-31-90096.
1.Cherevko A.A., Gologush T.S., Petrenko I.A., Ostapenko V.V., Panarin, V.A. Modelling of the arteriovenous malformation embolization optimal scenario //Royal Soc. Open Sci. 2020. Vol. 7. №. 7. P. 191992.
2. Khe A.K. et al. Monitoring of hemodynamics of brain vessels // J. App. Mech. Tech. Phys. 2017. Vol. 58. P. 763–770.
Татьяна Сергеевна Шарифуллина
Сеченовский университет
Моделирование напряженно-деформированного состояния мягких тканей зачастую сопряжено с использованием гиперупругих моделей.
В работе описан метод приближенного решения задач нелинейной теории упругости в рамках конечных деформаций для случая гиперупругих материалов. Метод основан на использовании P1-конечных элементов и интерполяционных свойств барицентрических координат. Данный метод позволяет аналитически записать конечно-элементные уравнения для различных мер деформации, что способствует уменьшению объема вычислений, простоте и общности реализации по сравнению с классическими технологиями, основанными на использовании гессиана упругого потенциала.
Предложенный подход был реализован [2, 3, 4] для мер деформаций, основанных на полярном и верхнетреугольном (QR) разложении градиента деформации [1].
Отметим, что мера деформации, основанная на QR-разложении градиента деформации, позволяет использовать экспериментальные данные о механическом поведении материала непосредственно (без априорно заданного вида модели), что позволяет избежать неопределенности восстановления вида определяющих соотношений по экспериментальным данным.
В рамках развития модельно-независимых подходов (использующих таблично заданные экспериментальные данные) для моделирования напряженно-деформируемых состояний упругих тел предложенные методы протестированы на примере модельных задач для гиперупругих мембран [5].
Работа выполнена при финансовой поддержке РНФ (проект 19-71-10094).
Список литературы
1. Srinivasa A.R. On the use of the upper triangular (or QR) decomposition for developing constitutive equations for Green-elastic materials //International Journal of Engineering Science. 2012. Т. 60. С. 1-12.
2. Salamatova V.Y., Liogky A.A. Method of Hyperelastic Nodal Forces for Deformation of Nonlinear Membranes //Differential Equations. 2020. Т. 56. №7. С. 950-958.
3. Василевский Ю. В., Саламатова В. Ю., Лозовский А. В. О компактных формулах расчета деформаций мягких биологических тканей //Дифференциальные уравнения. – 2017. – Т. 53. – №. 7. – С. 935-935.
4. Саламатова В. Ю. Конечно-элементный метод расчёта трёхмерной деформации гиперупругих материалов //Дифференциальные уравнения. – 2019. – Т. 55. – №. 7. – С. 1023-1032.
5. Salamatova V. Y., Liogky A. A. Hyperelastic membrane modelling based on data-driven constitutive relations //Russian Journal of Numerical Analysis and Mathematical Modelling. – 2020. – Т. 35. – №. 3. – С. 163-173.
Виктория Саламатова
ИБХФ им. Н.М. Эмануэля РАН / РЭУ им. Г.В. Плеханова
В последние годы нанокомпозиционные волоконные материалы с ценными функциональными свойствами находят широкое применение в различных областях, в том числе: материалы для фотоники, генной терапии, биомедицины [1]. Большой научный и практический интерес представляет исследование структурных особенностей биополимерных волокон, позволяющих варьировать их важнейшие свойства и эксплуатационные характеристики. Одним из наиболее перспективных методов получения материалов с контролируемой морфологией и геометрией волокон в слое материала является электроформование [2]. Целью данной работы было рассмотрение особенностей структуры ультратонких волокон на основе поли-3-гидроксибутирата (ПГБ) и установление деформационных свойств полимерных волокон.
В результате серии экспериментов в различных средах (вода, воздух, многоатомные спирты), моделирующих условия, в которых могут оказываться волоконные тканеинженерные конструкиции в период эксплуатации, были установлены ключевые закономерности, позволяющие детально описать деформационные процессы, как в материале, так и в одельных волокнах.
Было установлено, что деформационные свойства волокон на основе ПГБ в большой степени зависят от организации надмолекулярной структуры. Выработка волокон методом электрофоромования способствует формированию локальных напряжений в макромолекулях полимера [3]. Воздействие на эти области за счет предварительной обработки или помещение материала в жидкие среды ведет к реорганизации надмолекулярной структуры и снятию этих напряжений, что обуславливает существенный рост всех физико-механических характеристик.
Полученные данные позволяют моделировать надмолекулярную стурктуру волокон на основе ПГБ для медицинских изделий таким образом, чтобы обеспечить заданные физико-механические свойства, а также с высокой точностью предсказать характер деформирования и разрушения материала.
1. Ding J., Zhang J., Li J., Li D., Xiao C., Xiao H., Yang H., Chen X. Electrospun polymer biomaterials. // Progress in Polymer Science, 2019, 90, pp. 1-34.
2. Филатов Ю. Н. Электроформование волокнистых материалов (ЭФВ-процесс). М.: Нефть и Газ, 1997.
3. Tyubaeva P., Zykova A., Podmasteriev V., Olkhov A., Popov A., Iordanski A. The investigation of the structure and properties of ozone-sterilized nonwoven biopolymer materials for medical application. // Polymers, V. 13, № 8, 2021, Номер статьи 1268.
Полина Михайловна Тюбаева
Институт механики МГУ, Москва
Модели механики контактных взаимодействий находят широкое применение при анализе взаимодействия медицинских инструментов с различными биологическими тканями, а также при разработке методов оценки механических характеристик сложных биологических объектов. Полученные знания имеют самостоятельный интерес, а также используются для разработки сложных робототехнических устройств для проведения различного рода малоинвазивных операций, в том числе с возможностью тактильного очувствления действий хирурга во время операций на различных органах.
Излагаются методы решения контактных задач о взаимодействии медицинского инструмента с мягкой упругой тканью, основанные на подходах механики дискретного контакта [1]. Анализируется влияние формы поверхности инструмента на распределение контактных давлений и на зависимость внедрения инструмента от приложенной к нему силы [2]. Ставятся вопросы выбора формы поверхности инструмента, обеспечивающей более равномерное распределение действующей нагрузки по поверхности инструмента.
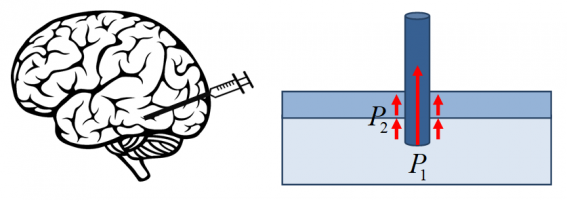
При разработке позиционирующего медицинского оборудования возникает необходимость описания процесса взаимодействия иглы с биологической тканью (рис.1а) или фантомом, моделирующим механическое поведение мягких тканей. Процесс взаимодействие иглы с мягкими тканями включает в себя несколько стадий: сжатие мягкой ткани, прокол, углубление иглы в ткань на большую глубину, удержание ее на этой глубине и дальнейшее ее извлечение. При этом необходимо учитывать такие механические процессы, происходящие в ткани, как упругое сжатие, разрушение поверхностного слоя, большие деформации, релаксация напряжений, трение (рис.2б). Для описания механического поведения биологической ткани применяются упруго-вязко-пластические модели. Использование аналитических методов позволяет получить зависимости силы от времени (или глубины внедрения) в течение всего процесса взаимодействия.
Важным применением методов механики в медицине является также разработка приборов для определения механических свойств биологических тканей [3].
1. Горячева И.Г. Механика фрикционного взаимодействия. М.: Наука. 2001. 478 с.
2. Яковенко А.А. Моделирование контактного взаимодействия захватывающего инструмента с биологической тканью. Российский журнал биомеханики. 2017, т.21, № 4, сс.418-428.
3.M.M. Gubenko, A.V. Morozov, A.N. Lyubicheva, I.G. Goryacheva, M.Z. Dosaev, M.-Sh. Ju, Ch.-S. Yeh, F.-Ch. Su. Video-tactile pneumatic sensor for soft tissue elastic modulus estimation. BioMedical Engineering. 2017, V.16, № 94
Ирина Георгиевна Горячева
МГУ имени М.В.Ломоносова
Была поставлена глобальная задача моделирования грудной клетки для применения в лечении пациентов с килевидной деформацией. Подобное моделирование, особенно с помощью программ конечно-элементного анализа1, является своевременным и отвечающим запросам современной медицины.
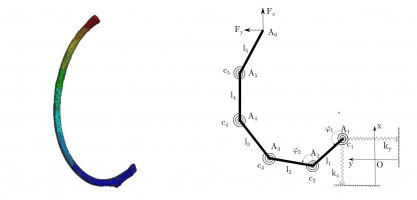
В данном исследовании была построена механическая модель плоского ребра под нагрузкой, приложенной к его концу. Модель ребра состоит из 5 абсолютно твердых стержней, соединенных между собой спиральными пружинами и расположенных в одной плоскости. Спиральная пружина в начале первого стержня препятствует повороту этого стержня в плоскости. Также начало первого стержня соединено цилиндрическими пружинами с двумя перпендикулярными друг другу неподвижными плоскостями, что моделирует податливость в синовиальном суставе головки ребра. В изначальном положении все пружины не деформированы.
Для данной системы были получены уравнения равновесия под действием плоской силы, приложенной к свободному концу ребра. При известных жесткостях пружин и геометрических параметрах ребра данная система позволит быстро вычислять деформированное состояние ребра. Геометрические параметры, а именно длины стержней и углы между ними в недеформированном состоянии были найдены с помощью специализированной медицинской программы 3D Slicer, позволяющей сегментировать необходимые области по КТ сканам пациентов. Для нахождения решения уравнений равновесия необходимо идентифицировать параметры – жесткости пружин.
Жесткости пружин находились из гипотезы равенства перемещений свободного конца ребра в стержневой модели и в модели ребра как криволинейной линейно-упругой однородной изотропной плоской балки. Перемещения в балочной модели находились численно с помощью интеграла Мора.
Также было произведено моделирование ребра в программе конечно-элементного анализа Ansys. Ребро моделировалось линейно-упругим изотропным материалом. Механические характеристики материала, такие как модуль Юнга, были взяты из литературы1. Для конечно-элементной модели было найдено напряженно-деформированное состояние. Различие перемещений свободного конца в рассмотренных моделях составляет не более 10%.
Иван Викторович Алпатов
Донской государственный технический университет
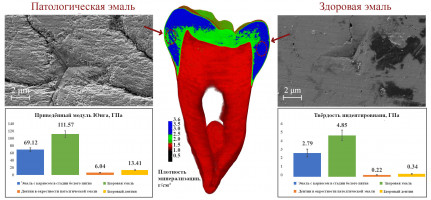
Начальная стадия кариеса характеризуется деминерализацией эмали (как в коронковой части, так и в пришеечной) без кавитации. При этом происходит повреждение основного структурного компонента твёрдых тканей зуба – кристаллов гидроксиапатита, которые либо растворяют центры кристаллов, либо участки на их периферии [1]. Подобная патология называется кариесом в стадии белого пятна, причем в некоторых случаях в процесс может быть также вовлечен дентин в окрестности деминерализованной эмали. В клинической практике все большее распространение получают малоинвазивные методы лечения ранних стадий кариеса. Использование реминерализующих агентов направлено на восстановление естественной структуры эмали, тогда как методы инфильтрации позволяют избежать использования стоматологического бора и анестезии, сводя удаление тканей зуба к минимуму. Принимая результаты исследований характеристик тканей в областях кариеса в стадии белого пятна как контрольные, стоматологи могут in vitro отслеживать изменения, возникающие в патологических тканях после минимально инвазивного лечения.
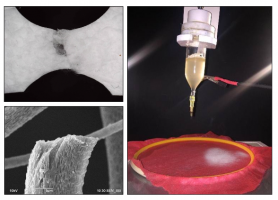
В настоящей работе изучен комплекс характеристик (плотность минерализации, приведенный модуль Юнга, твердость индентирования, средняя шероховатость, максимальная высота шероховатости) и особенностей (структура поверхности, молекулярный состав, ползучесть при индентировании) здоровых эмали и дентина, а также этих же тканей в окрестности области раннего на зубе человека (некоторые результаты представлены на Рисунке 1). Были использованы следующие методы: наноиндентировнаие (проведено в РЦКП НОЦ «Материалы» ДГТУ ), рентгеновская компьютерная микротомография, атомно-силовая, оптическая и сканирующая электронная микроскопия, а также рамановская спектроскопия [2].
Работа выполнена при финансовой поддержке гранта Правительства РФ № 14.Z50.31.0046.
1.Yanagisawa T., Miake Y. High-resolution electron microscopy of enamel-crystal demineralization and remineralization in carious lesions //Microscopy. 2003. Т. 52. №. 6. С. 605-613.
2.Sadyrin E., Swain, M., Mitrin, B., Rzhepakovsky, I., Nikolaev, A., Irkha, V., Yogina, D., Lyanguzov, N., Maksyukov, S. Aizikovich, S. Characterization of Enamel and Dentine about a White Spot Lesion: Mechanical Properties, Mineral Density, Microstructure and Molecular Composition //Nanomaterials. 2020. Т. 10. №. 9. С. 1889.
Евгений Валерьевич Садырин
Институт вычислительной математики им. Г.И. Марчука российской академии наук

Характеристики коаптации (соприкосновения) имеют решающее значение при оценке физиологической пригодности реконструированных аортальных клапанов. Коаптацию створок клапана можно оценить, используя для моделирования оболочечную или мембранную формулировки. В данной работе мы впервые провели сравнение обоих подходов с точки зрения коаптационных характеристик. Наша численная модель тонких оболочек основана на сочетании метода гиперупругих узловых сил и конечных элементов без вращения. Оболочечная модель проверена на нескольких популярных тестах для тонких оболочек, учитывающих изгибную жёсткость. Относительная погрешность относительно референсных решений не превышает 1-2%. Мы применили наши численные оболочечные и мембранные формулировки для моделирования закрытия идеализированного аортального клапана с различными моделями гиперупругости и их модулями сдвига. Характеристики коаптации оказались чувствительны к учёту изгибной жёсткости и почти нечувствительными к выбору упругих потенциалов, из числа нами рассматриваемых.
Алексей Андреевич Легкий
ФТИ им. А.Ф. Иоффе РАН, СПбПУ им. Петра Великого
Дентин – природный пористый материал с иерархической структурой, включающей в себя не менее семи масштабных уровней. Например, дентинные каналы представляют собой вытянутые микрополости диаметром 2-5 мкм, располагающиеся на расстоянии 10 мкм друг от друга.
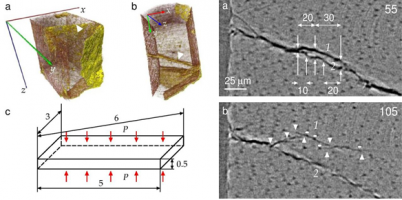
В течение многих десятилетий прочность и ударная вязкость дентина были в центре внимания обширных исследований, однако их происхождение до сих пор не ясно. Частично это объясняется тем, что ни один метод визуализации не может отображать по крайней мере несколько структурных уровней дентина одновременно. Среди других важных тем, связанных с дентином человека, большой интерес вызывают процессы распространения в нем трещин. Исследования в этой области показали, что основным механизмом упрочнения является перекрытие трещин связками без трещин [1]. Так называемые «мостики» неповрежденного материала наблюдались непосредственно с помощью оптического и сканирующего электронного микроскопов и рентгеновской томографии [2]. Были представлены доказательства взаимодействия каналов с растущей микротрещиной. Однако не было предложено никакого механизма, объясняющего, как образуются вторичные (сателлитные) микротрещины и как микротрещина притягивается к каналу.
В данной работе представлены экспериментальные доказательства и теоретическая модель распространения трещин поперечного сдвига в дентине при одноосном сжатии. Экспериментальные наблюдения образцов дентина размером несколько миллиметров проводились методом рентгеновской томографии с использованием синхротронного излучения. 2D-срезы (томограммы) выявили доминирующие и сателлитные трещины поперечного сдвига в образцах дентина после нагрузки: оба типа трещин распространяются по дентинным каналам [3].
Сделан вывод о том, что растягивающие напряжения на поверхности дентинных каналов, расположенных вблизи вершины заторможенной магистральной трещины, достаточны для образования сателлитных трещин. Процесс раскрытия трещины в дентине происходит за счет последовательных перемещений ее вершины от одного канала к другому (рис. 1) в плоскости действия максимальных локальных растягивающих напряжений; это сопровождается раскрытием сателлитных трещин в окрестности вершины заторможенной магистральной трещины.
Работа выполнена при поддержке гранта Российского фонда фундаментальных исследований № 19-29-12041.
1.Kinney J. H. et al. Age-related transparent root dentin: mineral concentration, crystallite size, and mechanical properties //Biomaterials. – 2005. – Т. 26. – №. 16. – С. 3363-3376.
2.Nalla R. K., Kinney J. H., Ritchie R. O. Effect of orientation on the in vitro fracture toughness of dentin: the role of toughening mechanisms //Biomaterials. – 2003. – Т. 24. – №. 22. – С. 3955-3968.
3.Argunova T. S., Gudkina Z. V., Gutkin M. Y. A Model of Microcrack Development in Human Tooth Dentin Using Data of Microtomography //Technical Physics Letters. – 2020. – Т. 46. – №. 5. – С. 505-509.
Жанна Вадимовна Гудкина
Пермский национальный исследовательский политехнический университет
За последние 10 лет распространенность онкологических заболеваний желчевыводящих путей увеличилась примерно в 2 раза. Одним из решения проблемы удаления желчного протока, пораженного опухолью, может стать его замена искусственно созданным биополимерным каркасом (скаффолдом). Существует несколько способов создания биоматериалов для замены тканей и органов (3d биопечать, электроформование и т.д.).
В ходе данной работы было выполнено создание двухслойного волокнистого каркаса общего желчного протока методом электроформования. Основа этого метода заключается в том, что электрическое напряжение прикладывается к раствору полимера, который при помощи дозатора подается через капилляр, а высокое напряжение индуцирует в растворе полимера одноименные электрические заряды, которые, в результате кулоновского электростатического взаимодействия, приводят к вытягиванию раствора полимера в тонкую струю. В качестве материала для воссоздания органа использовались биосовместимые и биоразлагаемые полимеры: поли-L-лактид, хитозан, поликапролактон и диацетат целлюлозы. Производилось сравнение микроструктуры данных материалов с помощью микроскопии. Для оценки распределения волокон использовались методы математического моделирования и статистической механики. Также была произведена оценка механических свойств полученных протоков.
Было показано что, наиболее подходящими для создания каркаса общего желчного протока являются поли-L-лактид и поликапролактон, прочные волокнистые структуры которых создавались методом электроформования. Данный каркас можно эффективно использовать в медицине, а его механические свойства дают результаты сопоставимые с данными о натуральном органе.
Дарья Ивановна Спорышева
Новосибирский Государственный Университет
Вступление
Аорта - самый крупный сосуд кровеносной системы человека, который играет важнейшую роль в процессе кровоснабжения всех органов и тканей. Любые поражения аорты приводят к тяжелым последствиям и даже к летальному исходу. При повреждении стенки и разрыве аорты вероятность летального исхода достигает 90% даже при экстренной госпитализации и хирургическом вмешательстве.
Основная причина разрыва аорты – возникновение аневризмы, которая чаще всего возникает набрюшном отделе аорты. Риск разрыва при наличии аневризмы может усугубляться сопутствующими сердечно-сосудистыми заболеваниями - стенозом, атеросклерозом, которые вызывают патологические изменения стенок сосуда, приводящие к ухудшению упругих свойств тканей и постепенной его деградации.
Материалы и методы
Целью данной работы является экспериментальное изучение механических свойств тканей аорты с аневризмами и сопутствующими патологиями. Для этого использовались ткани аорты, иссеченные во время кардиохирургических операций в НМИЦ им. Мешалкина. В условиях, обеспечивающих наилучшее сохранение механических свойств этих сосудов, образцы аорты доставляются в лабораторию Института гидродинамики и науки им. М. А. Лаврентьева СО РАН, где проводятся эксперименты. Перед экспериментом полученную ткань разрезают на несколько образцов, по возможности обращая внимание на направление кровотока. После этого измеряются параметры образца, и он помещается в одноосную разрывную машину INSTRON 5944.
Результаты и обсуждение
Полученные результаты были обработаны, для каждого эксперимента построены диаграммы деформация-напряжение. Такие данные, как предельное напряжение и деформация, а также модуль Юнга были определены для каждого типа патологии и статистически проанализированы.
Анна Игоревна Липовка