Асимптотическое поведение локализованного возмущения слоя вязкой жидкости на наклонной плоскости

Автор: Юлия Сергеевна Зайко

Соавторы: А.Г. Куликовский

Организация: Математический институт им. В.А. Стеклова Российской академии наук, Москва

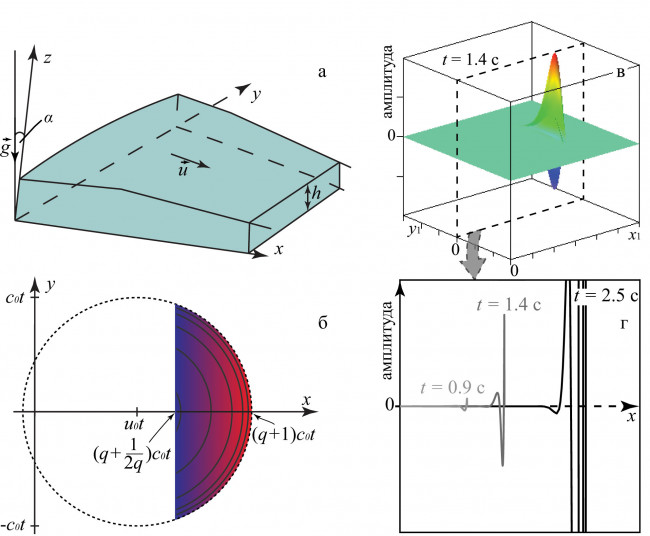
Течения потоков жидкости по наклонным поверхностям часто встречаются в природе и различных технических приложениях. С первой четверти XX века устойчивость таких потоков и развитие возмущений в них активно изучались аналитически, экспериментально, а позже и численно (см., например, [1, 2]). В настоящей работе аналитически в линейном приближении с помощью метода перевала изучается асимптотическое поведение локализованного по пространству и времени возмущения слоя линейно-вязкой жидкости на наклонной плоскости. Течение описывается уравнениями в гидравлическом приближении, то есть осреднёнными по глубине уравнениями МСС с учётом некоторых предположений (см., например, [3]). Рассматривается однородный неустойчивый поток на склоне постоянного уклона α (рис. 1а). Ранее эволюция трёхмерного локализованного возмущения открытого потока на вертикальной стенке исследовалась методом перевала в работах [2, 4]. В [2] (Глава 11, с. 327) рассматривалось течение, описываемое обобщённым уравнением Курамото-Сивашинского; в [4] — течение, описываемое системой уравнений Капицы-Шкадова.

Локализованное возмущение представляется суммой двойных интегралов Фурье, где интегрирование ведётся по всем вещественным волновым числам k_x, k_y (k_x, k_y — компоненты волнового вектора), суммирование — по корням дисперсионного уравнения (см. [5]). В начальный момент времени возмущение задаётся дельта-функцией. С помощью метода перевала определены размеры и форма области пространства, занятой растущим возмущением (рис. 1б), и поведение волны внутри этой области. (Обозначения: g — ускорение свободного падения, h — глубина потока, q = u₀/c₀, c₀ = (gh₀cosα)^1/2, u₀ — скорость невозмущённого потока, направленная вдоль оси x, нижний индекс «0» отмечает величины, относящиеся к невозмущённому течению.) Возмущение растёт внутри сегмента круга радиуса c₀t с центром в точке x = u₀t, y = 0. Гребни растущих волн — дуги окружностей с центром в той же точке (показаны серым на рис. 1б). Длина волны стремится к нулю при приближении к точке x = (q+1)c₀t. Фазовая скорость возмущения превосходит групповую. Визуализация возмущения в пространстве приведена на рис. 1в.

Исследование выполнено за счет гранта Российского научного фонда (проект № 19-71-30012).

1. Алексеенко С.В., Накоряков В.Е., Покусаев Б.Г. Волновое течение пленок жидкости. — Новосибирск: ВО «Наука». Сибирская издательская фирма, 1992. — 256 с.

2. Chang H.-C., Demekhin E.A. Complex Wave Dynamics on Thin Films. D. Möbius and R. Miller. Elsevier. Amsterdam. 2002.

3. Эглит М.Э. Неустановившиеся движения в руслах и на склонах. — М.: Изд-во Моск. ун-та, 1986. — 96 с.

4. Demekhin E.A., Kalaidin E.N., Kalliadasis S., Vlaskin S.Yu. Three-dimensional localized coherent structures of surface turbulence. II. Λ solitons // Phys. Fluids. 2007. V. 19. 114104.

5. Zayko J., Eglit M. Stability of Downslope Flows to Two-Dimensional Perturbations. // Phys. Fluids. 2019. V. 31. 086601.