Исследование неустойчивости упругой трубки бесконечной и конечной длины с протекающей внутри псевдопластической жидкостью
Автор: Анастасия Борисовна Подопросветова
Организация: МГУ имени М.В. Ломоносова
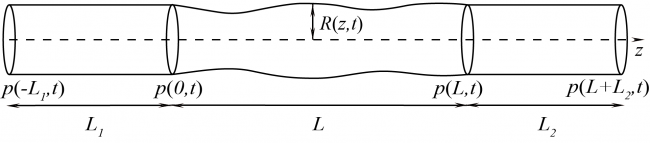
В биологических приложениях при течении жидкостей в моделях кровеносных сосудов возникают различные явления, которые оказывают влияние на характер течения и на деформацию стенок, что влечёт за собой дисфункциональные изменения в организме человека или животного.
Ранее в литературе исследовались, в основном, течения ньютоновской (линейно-вязкой) или идеальной жидкости [1, 2]. Хотя, кровь в средних и мелких сосудах обладает неньютоновскими свойствами. При этом одномерное моделирование течения крови по кровеносным сосудам является удобным инструментом для изучения динамики биологической жидкости в системе кровообращения.
Данное исследование проводилось классическими методами теории устойчивости, на основе ранее разработанной одномерной модели [3, 4]. Для трубок бесконечной длины рассматривались решения в виде бегущих волн и выводилось дисперсионное уравнение. Анализом его корней находились области неустойчивости в пространстве параметров.
Поскольку критерий устойчивости для сколь угодно большой длины трубки не совпадает с критерием устойчивости для бесконечно длинной трубки, то для определения границ устойчивости задача была исследована на нахождение области глобальной неустойчивости. В данном случае использовался асимптотический метод глобальной неустойчивости, разработанный А.Г. Куликовским [5].
Кроме того, для трубок конечной длины была решена задача на собственные значения. Граница устойчивости исследовалась численно с учетом упругости стенки трубы, продольного натяжения и длины трубки.
1.Grotberg J.B., Jensen O.E. Biofluid mechanics in flexible tubes // Ann. Rev. Fluid Mech. 2004. Vol.36. P.121–147.
2. Heil M., Hazel A.L. Fluid-Structure Interaction in Internal Physiological Flows // Ann. Rev. Fluid Mech. 2011. Vol.43. P.141–162.
3. Порошина А.Б., Веденеев В.В. Существование и единственность стационарного состояния упругой трубки при протекании через нее степенной жидкости // Российский журнал биомеханики. 2018. Т. 22. № 2. С. 196–222.
4. Веденеев В.В., Порошина А.Б. Устойчивость упругой трубки, содержащей текущую неньютоновскую жидкость и имеющей локально ослабленный участок // Труды МИАН. 2018.
Т. 300. С. 42–64.
5. Куликовский А.Г. Об устойчивости однородных состояний // Известия АН СССР. ПММ. 1966. Т. 30. Вып. 1. С. 148-153.
