О ПЕРИОДИЧЕСКИХ ПО ВРЕМЕНИ РЕШЕНИЯХ ЗАДАЧ ОДНОМЕРНОЙ ГАЗОВОЙ ДИНАМИКИ

Автор: Дмитрий Владимирович Украинский

Организация: Московский Государственный Университет имени М.В. Ломоносова

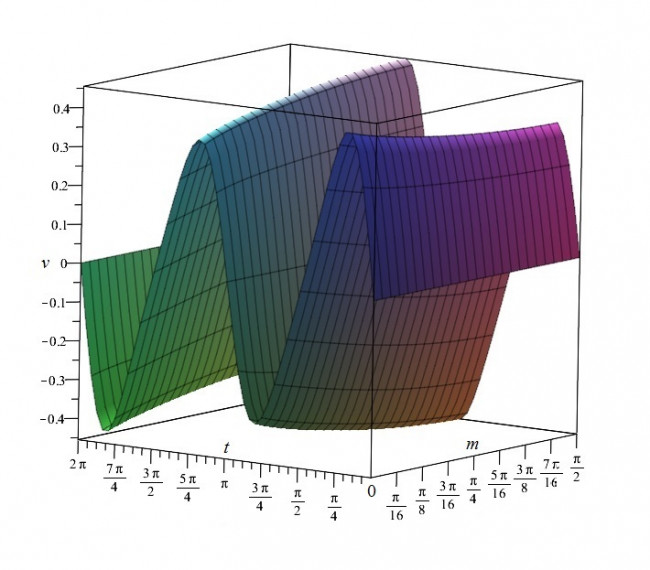
Рассматривается одномерное адиабатическое движение с плоскими волнами совершенного идеального газа в лагранжевых переменных. При этом уравнения движения сводятся с использованием массовой переменной к системе с квадратичной нелинейностью. Решение ищется, в частности, в виде рядов для закона движения газа и давления по степеням косинуса от временной переменной с коэффициентами, зависящими от массы. Для построения ряда требуется задать три первых коэффициента. Все остальные коэффициенты вычисляются рекуррентным образом по заданным при условии ненулевой производной первого коэффициента ряда для закона движения. Преимуществом данного подхода перед разложением решения, например в тригонометрический ряд Фурье, является именно конечность алгебраических рекуррентных соотношений, связанных только с вычислением производных по массе. Проводятся численные расчеты, которые показывают высокую сходимость ряда при определенных ограничениях на производные от задаваемых коэффициентов. Дальнейшим обобщением развитого подхода является представление решения в виде суммы одного ряда по степеням косинуса и произведения синуса на другой аналогичный ряд. При этом условием рекуррентной разрешимости является неравенство нулю разности квадратов производных первых членов, указанных выше рядов. Развивается соответствующий вычислительный процесс. Приводятся примеры, не содержащие особенностей.

Работа частично поддержана РФФИ (проект 17-01-00037)

Рис. Пример графика скорости потока на периоде