МГТУ им. Н.Э. Баумана; ИМАШ им. А.А. Благонравова РАН
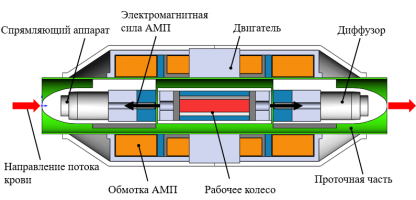
На рисунке: Схема НВК в разрезе с указанием основных функциональных элементов и электромагнитой силы АМП
Искусственный желудочек сердца (ИЖС) находит применение в терапии сердечной недостаточности терминальной стадии. Роль рабочего звена ИЖС, непосредственно обеспечивающего транспорт крови в обход желудочка сердца, играет насос вспомогательного кровообращения (НВК). В настоящее время наблюдается тенденция по переходу от традиционных подшипниковых узлов скольжения к магнитному подвесу. Данный переход связан с уменьшением гемолиза крови, потерь мощности насоса и риска тромбообразования при использовании магнитного подвеса [1].
Магнитный подвес должен обеспечивать контролируемую динамику рабочего колеса (РК) при действии внешних сил, имея при этом минимально возможные габариты. Применительно к проектированию НВК внешние силы обусловлены набегающим потоком крови. В работе [2] представлена оценка действующих на рабочее колесо гидродинамических сил, которая получена посредством решения стационарной CFD‑задачи.
В данной работе рассмотрен осевой тип НВК. Его вид в разрезе с указанием характерных элементов приведён на рисунке. Согласно выбранной схеме, поток крови набегает вдоль оси насоса на его составляющие, расположенные в проточной части: спрямляющий аппарат (СА), рабочее колесо и диффузор. Лопасти РК условно не показаны. РК приводится во вращение электродвигателем, его положение контролируется магнитным подвесом. Здесь и далее подразумевается именно активный магнитный подвес (АМП). АМП установлен в торцевые части СА и диффузора.
Для конструирования конфигурации магнитного подвеса применена методика, изложенная в [3]. Определены число витков в катушке АМП, сила тока, осевое усилие.
Для уточнения характерных размеров разрабатываемой конфигурации решена задача оптимизации по критерию минимума геометрических параметров при выполнении требования по осевой нагрузке. Варьируемыми параметрами представлены геометрические размеры, число витков, сила тока. Для достижения цели была построена конечноэлементная модель АМП. На её основе решена задача расчёта распределения магнитного поля АМП и генерируемых сил в стационарной постановке, а также проведена оптимизация по обозначенному выше списку параметров. Результат работы выражен определёнными из анализа оптимальными характеристиками АМП в составе НВК.
Благодарность: Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 19-31-90051.
1. Hoshi H., Shinshi T., Takatani S. Third‐generation blood pumps with mechanical noncontact magnetic bearings //Artificial organs. – 2006. – Т. 30. – №. 5. – С. 324-338.
2.Скорюков С.В., Киселёв В.В., Крупнин А.Е., Банин Е.П., Гуськов А.М., Сорокин Ф.Д. Оценка гидродинамических сил на импеллере осевого насоса вспомогательного кровообращения с применением методов вычислительной гидродинамики // МИКМУС-2019 (Москва, 4-6 декабря 2019). – М: Изд-во ИМАШРАН. – 2020. – С. 406-409.
3. Журавлёв Ю.Н. Активные магнитные подшипники: теория, расчёт, применение. СПб: Политехника, 2003. 206 p.
Станислав Владимирович Скорюков
НИИ механики МГУ имени М.В. Ломоносова
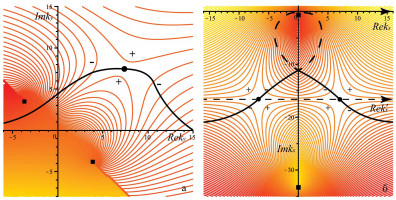
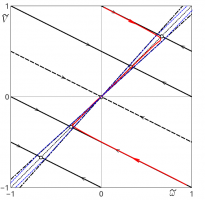
В докладе подробно описывается применение метода перевала к задаче об асимптотическом поведении локализованного возмущения потока ньютоновской среды на склоне постоянного уклона α. Движение жидкости происходит под действием силы тяжести и описывается уравнениями в гидравлическом приближении. Система уравнений имеет аналогию с системой уравнений газовой динамики, следовательно, является гиперболической. Все малые возмущения такой системы лежат внутри конуса характеристик (x-c0t)2+y2≤c02t2, который выделяет на плоскости U1,V1 круг единичного радиуса с центром в точке (q,0). Здесь U1=U/c0, V1=V/c0, q=u0/c0, x=Ut, y=Vt, u0 — модуль скорости невозмущённого течения, с0 = (ghcosα)1/2 — скорость распространения малых мелкомасштабных возмущений относительно частиц среды, оси x, y лежат в плоскости склона, невозмущённая скорость направлена вдоль оси x. С помощью метода перевала исследуется характер неустойчивости (конвективная или абсолютная неустойчивость) вдоль каждого луча x=Ut, y=Vt (U, V вещественные). В рассматриваемой задаче метод перевала применяется сначала в комплексной плоскости ky, затем в комплексной плоскости kx (возмущение считается двумерным и задаётся интегралом Фурье по всем вещественным волновым числам). С помощью метода перевала найдена форма области, занятой растущим возмущением. На рис. приведены картины линий уровня функции Im(ω(kx,ky))=const в комплексных плоскостях волновых чисел kx, ky, показаны деформированные контуры интегрирования, проходящие через перевальные точки функции ω(kx,ky) (здесь ω — комплексная частота).
Работа частично поддержана грантами РФФИ (проекты № 18-31-20057, № 18-29-10020).
Юлия Сергеевна Зайко
МГУ имени М.В. Ломоносова
В докладе рассматриваются новые примеры применения метода асимптотического разделения движений для исследования динамики систем твердых тел. В каждой задаче естественным образом возникает малый параметр, при нулевом значении которого уравнения допускают один или несколько первых интегралов. При возмущении системы значения этих интегралов медленно меняются с течением времени, что позволяет производить качественный анализ решений полной системы.
В задаче о движении экипажа повышенной маневренности с омниколесами выявляется связь между динамической системой, описывающей его движения по инерции [1], и классической задачей неголономной механики о коньке Чаплыгина. Исследуется механизм потери устойчивости прямолинейных движений такого экипажа (по результатам курсовой работы студента механико-математического факультета Я.Э. Минькова).
В задаче о торможении однородного упругого деформируемого цилиндра по полупространству из того же материала [2] рассматривается два варианта возмущений: однородный цилиндра из вязкоупругого материала [3] и неоднородный упругий цилиндр(по результатам курсовой работы студентки механико-математического факультета А.Н. Зотовой). В каждой из представленных задач методом введения быстрых и медленных переменных удается выявить качественные свойства решений возмущенных задач.
Работа выполнена при поддержке гранта РФФИ 19-01-00140.
Александра Александровна Зобова
НИИ механики МГУ
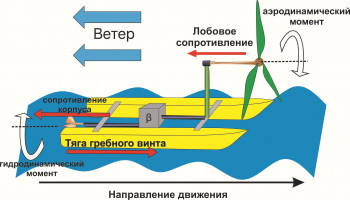
Рассматривается математическая модель одноосного судового ветродвигателя с трансмиссией, продолжающая исследование [1]. Основу такого ветродвигателя составляют два горизонтально расположенных вала, соединённых между собой трансмиссионным блоком передачи вращения (рис.1). На конце верхнего вала закреплён ветроприёмный пропеллер, а на конце нижнего – подводный гребной винт.
Для описания пропеллера и гребного винта рассматриваются результаты реальных экспериментов для корабельных гребных винтов и пропеллеров от ветроэнергетических установок [2,3].
В работе проанализировано влияние учёта гидродинамического сопротивления корпуса, найдено оптимальное значение коэффициента передачи вращения от пропеллера к винту, при котором катамаран развивает теоретически максимальную скорость против ветра. Исследованы преимущества разных коэффициентов передачи и произведено численное моделирование выхода катамарана из состояния покоя на режим движения «против ветра» при помощи переключения передач. Найдена возможная стратегия перехода на предпочтительный режим движения.
1.Гарбуз М.А. Катамаран, движущийся против ветра при помощи противовращающихся пропеллерных ветродвигателей. – Сборник трудов КМУ 2018., Издательство Московского университета 2019, Москва, том 1, с. 69-76.
2. Я.И. Войткунский. Справочник по теории корабля. Том 1. Ленинград 1986.
3. Adaramola, M.S., Krogstad, P.A. Experimental in-vestigation of wake effects on wind turbine perfor-mance. Renewable Energy, 2011, 36(8), pp 2078-2086.
Михаил Андреевич Гарбуз
Институт физики атмосферы им.А.М.Обухова РАН
Эмиссия частиц микронного и субмикронного размера связывается с наличием потока сальтирующих частиц [1], усиливается с увеличением высоты эффективной шероховатости [2] и имеет кубическую зависимость от динамической скорости [3]. Другой механизм выноса связан с возникновением тепловых конвективных потоков над поверхностью [4]. Соотношение доли падающих частиц к частицам, выносимым с поверхности, возрастает при движении вверх по наветренному склону дюны [5, 6]. Этот факт позволяет сделать вывод о преобладании вертикального механизма выноса частиц над сальтационным (ударным). Проведены исследования условий отрыва отдельных частиц и влияния на этот процесс возникновения и роста эоловых микроструктур.
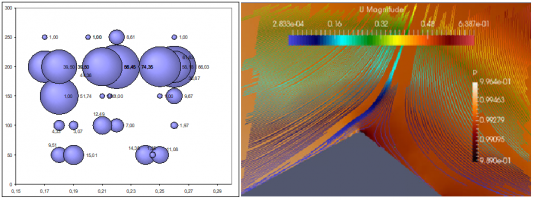
Рассмотрено обтекание микроряби высотой 0,1-1 мм при скоростях воздушного потока до 4 м/с на высоте 1-2 см с использованием открытого пакета LES model in openFOAM. Добавление на шероховатую поверхность обтекаемой эоловой структуры борозд у вершины приводит к смещению точки отрыва восходящих потоков, к изменению протяженности зоны рециркуляции и временных интервалов струйного усиления ветра у вершины, которое наблюдалось в частности в [7]. Эксперимента с добавлением борозды добавлены с учетом численных исследований для обтекания отдельных частиц для области 5х5х2 мм при скорости воздушного потока на верхней границе 2,8 м/с, выбираемой в соответствии с данными экспериментов в ветровом канале [7]. В зависимости от расстояния между частицами меняются выталкивающая сила, действующая со стороны воздушного потока, критическая скорость и начальные скорости вылета частицы. Как следствие, появляются области с различной вероятностью ветрового выноса, за счет чего, в частности, возникает эоловая рябь.
Исследование выполнено при поддержке проекта РНФ 20-17-00214.
- Houser C. A., Nickling W. G. Sedimentology. 2001. 48(2). 255-267.
- Martin R.L., Kok J.F. J. Geophys. Res. 2018. 123(7). 1546-1565.
- Shao Y., Raupach M. R., Findlater P. A. Effect of saltation bombardment on the entrainment of dust by wind //Journal of Geophysical Research: Atmospheres. – 1993. – Т. 98. – №. D7. – С. 12719-12726.
- Chkhetiani O. G. et al. Dust resuspension under weak wind conditions: direct observations and model //Atmospheric Chemistry and Physics. – 2012. – Т. 12. – №. 11. – С. 5147.
- Malinovskaya E.A. Izv. Atmos. Oceanic Phys. 2019. 55(2). 86-92.
- Neuman C.M.K et al. Sediment. 2000. 47(1). 211-226.
- Semenov O.E. Introduction to experimental meteorology and climatology of the sand storms. Almaty. 2011. p 580 (in Russian).
Елена Александровна Малиновская
Механико-математический факультет МГУ имени М.В. Ломоносова, Москва; НИИ механики МГУ имени М.В. Ломоносова, Москва
В рамках данного исследования был создан лабораторный макет ротора Савониуса. Прототип изучали в аэродинамической трубе НИИ механики МГУ при малых скоростях набегающего потока. Замерялись силы, действующие на ротор, и аэродинамический момент. В процессе эксперимента изменялись значения скорости набегающего потока и угловой скорости вращения ротора (в том числе исследовалось вращение в обратную сторону).
На базе полученных данных предложена модификация модели воздействия потока на ротор типа Савониуса, описанная в работах [1-3]. В рамках такой модели безразмерный коэффициент аэродинамического момента раскладывается в ряд Фурье. Получена зависимость коэффициентов ряда от безразмерной угловой скорости.
Такая модель позволяет существенно упростить проведение параметрического анализа для сложных механических систем, имеющих в своем составе ротор Савониуса. Это достигается благодаря расширению методов, применимых для решения такого рода задач за счет средств теоретической механики. Далее результаты можно уточнить с помощью классических методов теории сплошных сред, дающих более точное количественное совпадение, но слишком ресурсоемких для анализа динамики в широкой области параметров.
1. Мастерова А.А. Моделирование динамики малогабаритной ветроэнергетической установки на базе ротора Савониуса/ Труды конференции-конкурса молодых ученых. 13-17 октября 2017 г. / М.: Издательство Московского университета, 2018. – 140-147 с.
2. Мастерова А.А. Моделирование динамики колесной тележки, приводимой в движение с помощью ротора Савониуса/ Труды конференции-конкурса молодых ученых. 15-17 октября 2018 г. / М.: Издательство Московского университета – 98-105 с.
3. Мастерова А.А. Эмпирический подход к описанию воздействия потока на ротор Савониуса/ Тезисы конференции-конкурса молодых ученых Научно-исследовательского института механики МГУ имени М.В. Ломоносова 21-25 октября 2019 г. – с. 21.
Анна Андреевна Мастерова