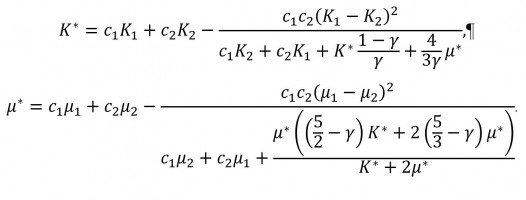НИИ механики МГУ, Москва
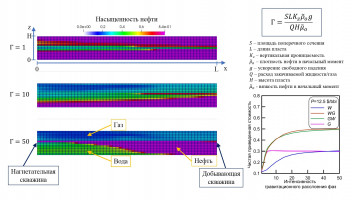
Исследуется влияние гравитационного расслоения фаз на оптимальные режимы водогазового воздействия на нефтяные пласты, предполагающего поочередную закачку воды и газа с целью вытеснения нефти. Целью данной работы является поиск безразмерного параметра, характеризующего гравитационное расслоение фаз, и исследование его влияния на коэффициент извлечения нефти и на значение чистой приведённой стоимости, характеризующей рентабельность водогазового воздействия. Для этого используется модель, объединяющая в себе физические и экономические параметры течения. Ранее рассматривалась аналогичная модель, описанная в [1], но для одномерного течения. В данной работе исследуются влияние стратификации фаз на оптимальные режимы водогазового воздействия.
Рассматривается двумерная модель нефтяного пласта заданной длины и высоты. На левой и правой границах расположены нагнетающая и добывающая скважины соответственно. В данной работе рассматриваются различные интервалы перфораций скважин и несколько различных режимов поочередной закачки смеси воды и углекислого газа. Параметр, характеризующий гравитационное расслоение фаз, выводится из системы уравнений, состоящей из законов сохранения массы каждой компоненты и закона Дарси. Исследуется влияние данного параметра на чистую приведённую стоимость закачки. Также рассмотрено несколько различных интервалов перфорирования скважин и исследовано их влияние на коэффициент извлечения нефти и чистую приведённую стоимость при различных значениях параметра подобия, характеризующего стратификацию фаз.
1. Afanasyev A., Andreeva A., Chernova A. Influence of oil field production life on optimal CO2 flooding strategies: Insight from the microscopic displacement efficiency // Journal of Petroleum Science and Engineering. 2021. V. 205. P. 108803
Анна Александровна Чернова
Институт механики и машиностроения ФИЦ КазНЦ РАН
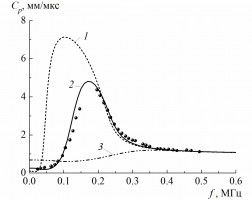
Покрытые вязкоупругой оболочкой пузырьки встречаются во многих областях. Но основное применение они нашли в биомедицине, где используются в качестве контрастных веществ для ультразвуковой диагностики [1]. В рамках данной работы получено модифицированное уравнение Релея-Ламба, учитывающее радиальные колебания пузырька газа, покрытого вязкоупругой оболочкой и находящегося в вязкоупругой среде. Учет вязкоупругости оболочки и несущей жидкости проводится на основе реологических моделей Кельвина-Фойгта и Максвелла. Для случая малых возмущений найдено дисперсионное уравнение, учитывающее межфазный теплообмен межу газом, вязкоупругой оболочкой и несущей средой. Проиллюстрировано влияние оболочки пузырьков, упругости несущей фазы на динамику акустических волн. В частности, на приведенном рисунке представлено влияние упругости несущей среды, оболочки пузырьков на зависимости фазовой скорости от частоты возмущений для смеси полидиметилсилоксана (PDMS RTV-615) с воздушными пузырьками. Дано сравнение теории с экспериментальными данными [2]. Параметры расчета и математическая модель представлены в работах [3, 4]. Кривая 1 построена без учета упругости несущей среды, кривая 2 – с учетом упругости несущей среды, кривая 3 – с учетом упругости несущей среды и при наличии вязкоупругой оболочки пузырьков. Как видно из рисунка, учет упругости несущей фазы приводит к сдвигу резонансной частоты возмущений (кривая 2), что также хорошо подтверждается экспериментальными данными. Дополнительный учет вязкоупругой оболочки приводит к еще большему значению резонансной частоты (кривая 3). Наличие оболочки пузырьков может привести также к исчезновению полосы непрозрачности у фазовой скорости (фазовая скорость не превысит скорость звука в несущей фазе во всем диапазоне частот). Это связано с тем, что оболочка пузырьков сдерживает пульсации включений. Пузырьки ведут себя как твердые частицы и, в связи с этим, происходит меньшее рассеяние акустической волны по сравнению с обычными пузырьковыми средами.
1.Goldberg B.B., Raichlen J.S., Editors F.F. Ultrasound contrast agents. Basic principles and clinical applications. Martin Dunitz, 2001.
2. Leroy V., Strybulevich A., Page J.H., Scanlon M. G. Influence of positional correlations on the propagation of waves in a complex medium with polydisperse resonant scatterers // Physical Review E. 2011. V. 83. P. 046605.
3. Губайдуллин Д.А., Федоров Ю.В. Волновая динамика покрытых оболочкой включений в вязкоупругой среде // ПМТФ. 2020. Т. 61. № 4. С. 22-30.
4. Gubaidullin D.A., Fedorov Yu.V. Acoustics of a viscoelastic medium with encapsulated bubbles // Journal of Hydrodynamics. 2021. V. 33. № 1. P. 55-62.
Юрий Валентинович Федоров
Институт механики и машиностроения ФИЦ Казанский научный центр РАН
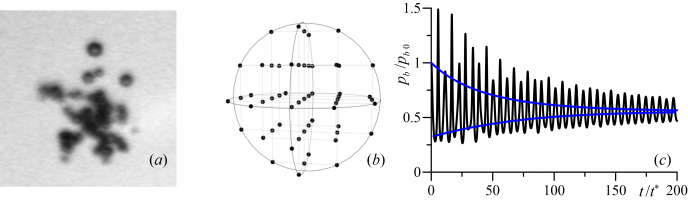
При достаточно больших концентрациях парогазовых пузырьков в жидкости значительную роль играет их гидродинамическое взаимодействие [1, 2]. В результате взаимодействия пузырьки могут сильнее расширяться и сжиматься, перемещаться по жидкости, образовывать кластеры (рис. а) и т.д. Эти и другие особенности взаимодействия пузырьков могут быть использованы в различных приложениях.
В настоящей работе изучается влияние взаимодействия между воздушными пузырьками в сферическом кластере (рис. b) в водоглицериновой смеси при мгновенном повышении их внутреннего давления. В экспериментах подобное повышение давления реализуется, например, при образовании пузырьков искровым или оптическим (лазерным) пробоем жидкости. До момента времени t=0 пузырьки и жидкость находятся в состоянии покоя, радиус пузырьков R0=0.25 мм, давление жидкости pL=1 бар, ее плотность rL=1156 кг/м3. Центры пузырьков расположены в узлах равномерной кубической сетки внутри сферической области так, что один из пузырьков располагается в центре этой области. Размер ячеек сетки 5 мм. При t=0 давление в пузырьках pb мгновенно повышается от равновесного значения pb0 до pb0+Dp, где Dp варьируется в диапазоне от 0.1 до 0.8 бар. Динамика пузырьков в кластере описывается системой ОДУ, представляющей собой частный случай уравнений работы [1].
Рис. (a) – фотография кластера пузырьков из эксперимента [2]; (b) – схема изучаемого кластера из 57 пузырьков; (c) – изменение безразмерного давления в центральном пузырьке кластера (черная кривая) и огибающие экстремальных значений давления в одиночном пузырьке (синие кривые), t*=R0(rL/pL)0.5.
Повышение давления в пузырьках приводит к возникновению их радиальных колебаний, которые постепенно затухают под влиянием сжимаемости и вязкости жидкости. В результате система со временем переходит в новое равновесное состояние. Процесс перехода в новое равновесное состояние пузырьков кластера во многом отличается от перехода одиночного пузырька, что обусловлено взаимодействием пузырьков. В частности, колебание давления в пузырьках кластера затухает существенно немонотонно (рис. c). При этом у пузырьков в кластере скорость затухания и частота колебаний давления значительно меньше, чем у одиночного пузырька. Максимальные давления в пузырьках центральной области кластера принимают значения, заметно превосходящие максимальное давление в одиночном пузырьке.
1. Aganin A.A., Davletshin A.I. Equations of interaction of weakly non-spherical gas bubbles in liquid // Lobachevskii Journal of Mathematics. 2018. V. 39. № 8. P. 1047-1052.
2. Luther S. Theoretische Beschreibung und experimentelle Untersuchung raum-zeitlicher Strukturbildung in akustischen Kavitationsblasenfeldern. – Niedersächsische Staats- und Universitätsbibliothek, 2000.
Анас Ильгизович Давлетшин
Институт физики атмосферы им.А.М.Обухова РАН
Рис 1. Изменение турбулентной энергии при движении частиц вблизи препятствия, на наветренном и подветренном склонах эоловой структуры
Пыль на поверхности движущихся крупных частиц размером 70-300 мкм (сальтаций и перекатывания) в результате взаимодействий отделяется при трении или ударе [1]. Размер генерируемых микрочастиц определяется углами падения сальтирующих и перекатывающихся частиц, изменением направления ветра по отношению к грядам эоловых структур [2]. Исследуется влияние препятствия на движение воздушного потока со взвешенными в нем частицами над шероховатой поверхностью (при скоростях на высоте 1 м: 4,6; 5,07; 5,76; 6,22; 6,91 м/с. Используется Лагранжево-Эйлеровая модель, реализованная в открытом пакете OpenFoam. Рассмотрено влияние направления ветра по отношению к эоловой структуре, при изменении углов наклона ее поверхностей наветренного и подветренного склонов к горизонту, и, соответственно, их протяженностей.
Движение частиц над препятствием удлиняет зону рециркуляции, уменьшает высоту расположения локальной зоны увеличения турбулентной энергии, приближая ее к поверхности. Так как размеры и форма эоловой структуры, а также скорость воздушного потока влияют на протяженность и отдаленность от вершины зоны рециркуляции, то меняются траектории и скорости движения частиц разного размера над подветренным склоном. Чем больше удаленность траекторий движения частиц от центра зоны рециркуляции, тем больше дополнительный разгон и скорость их падения на поверхность. Вследствие возмущений, вызванных движениями частиц, в области за эоловой структурой возрастает турбулентная диффузия, что способствует интенсификации выноса пылевого аэрозоля за пределы слоя сальтации. Ускорение частиц приводит к усилению т.н. эффекта "разбрызгивания", а, следовательно, к увеличению числа откалываемых микрочастиц.
Само же изменение высоты эоловой структуры и ее ориентации по отношению к воздушному потоку влияет на интенсивность процессов перекатывания частиц по наветренному склону, что отражается в явлениях стирания мелкой фракции микрочастиц поверхности более крупных элементов. Соотношение типов перемещения частиц на наветренном и подветренном склонах, и, соответственно, процессов стирания и откалывания, определяется нелинейной связью углов наклона поверхности и скорости воздушного потока. Это влияет на вид функции распределения микрочастиц по размерам.
1. Liu Y., Fang H., Huang L., He G. Numerical simulation of the production of three-dimensional sediment dunes // Physics of Fluids. 2019. Vol. 31, no. 9. P. 096603.
2. Малиновская Е.А., Чхетиани О.Г., Максименков Л.О. Влияние направления ветра на распределение эоловых микрочастиц по размерам // Физика атмосферы и океана [в печати].
Елена Александровна Малиновская
ИМСС УрО РАН, ПГНИУ
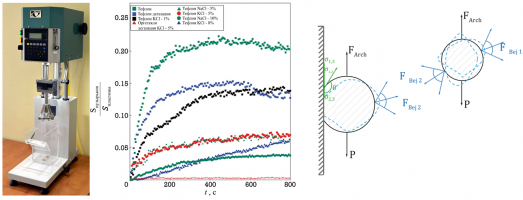
В настоящей работе экспериментально исследуется возникновение, динамика и взаимодействие парогазовых пузырьков, возникающих в следствии коалесценции кавитационных пузырьков при ультразвуковом (УЗ) воздействии, с поверхностью твердого тела при кондиционировании флотационной пульпы и последующей флотации.
В экспериментах использовалась лабораторная флотомашина ФМП-Л1 оснащенная аэрационным механизмом пневмомеханического типа с прямым (безременным) электроприводом. Для проведения кондиционирования исследуемой пульпы использовался сонохимический реактор представляющий собой кювету, изготовленную из оргстекла толщиной 3 мм. В центральной части дна кюветы располагался источник УЗ. Для визуализации пузырьков в различных экспериментах использовался либо лазерный нож, создаваемый цилиндрической линзой и зеленым лазером KLM 532, либо светодиодный колимированный источник света. Для регистрации динамики пузырьков использовалась высокоскоростная камера Basler A504kc с телецентрическим макро-объективом, и зеркальная камера Nikon D7200 [1, 2].
Во всех сериях эксперимента гидрофобность поверхности способствовала прикреплению к ней пузырьков. Диаметр прикрепленных пузырьков непрерывно увеличивался в течение всего времени ультразвукового облучения за счет коалесценции с пузырьками возникающих в результате акустической кавитации. Парогазовые пузырьки оставались прикрепленными к гидрофобной поверхности и не всплывали, так как поверхностные силы превышали силу Архимеда. Динамика парогазовых пузырьков на гидрофильной поверхности качественно отличается от динамики пузырьков на гидрофобной поверхности.
Исследование выполнено при финансовой поддержке из средств гранта Российского научного фонда (проект № 20-69-46066)
1.Rybkin K. A. et al. Experimental study of formation and dynamics of cavitation bubbles and acoustic flows in NaCl, KCl water solutions // Journal of Physics: Conference Series. IOP Publishing, 2017. Т. 879. №. 1. С. 012026.
2.Fattalov, O., Lyubimova, T., Rybkin, K., & Kuchinskiy, M. (2021). Experimental Study of the Processes of Formation, Drift and Levitation of Vapor–Gas Bubbles in Water Containing Surfactant Under the Action of Ultrasound. Microgravity Science and Technology, 33(2), 1-7.
Константин Анатольевич Рыбкин
Институт механики и машиностроения – обособленное структурное подразделение ФИЦ КазНЦ РАН
Воздействие волновых процессов на ограниченную многофазную среду приводит к возникновению нелинейных явлений [1]. В работе [2] рассматриваются резонаторы в виде конуса, рупора или колбы. Создаваемые колебания сильно влияют на поведение частиц в данных объемах [3]. Например, изменению поля средней температуры [4], усилению перемешивания [5], ускорению осаждения и увеличению теплообмена среды [6]. Ранее рассматривались осаждения частиц аэрозоля при резонансных колебаниях в трубах [7].
В данной работе исследуется динамика аэрозоля в резонаторе прямоугольного сечения вблизи резонансной частоты. Получены значения колебаний давления газа вблизи резонанса. Выявлено, что начальная концентрация капель монотонно уменьшается со временем по сравнению с естественным осаждением.
Исследование выполнено за счет гранта Российского научного фонда (проект № 20-79-00144).
1.Нигматулин Р.И. Динамика многофазных сред // Москва: Наука. 1987. Т. 1. 464 с.
2.Mortell M.P., Seymour B.R. Nonlinear resonant oscillations in closed tubes of variable cross section // J. Fluid Mech. 2004. V. 519. P. 183–199.
3.Davidson G.A., Jager W. Turbulence and aerosol coagulation in high intensity sound fields // J. Sound and Vibr. 1980. V. 72. №. l. P. 123.
4.Daru V., Baltean-Carles D., Debesse P., Gandikota G. Two-dimensional numerical simulations of nonlinear acoustic streaming in standing waves // Wave Motion. 2013. V. 50. P. 955–963.
5.Аганин А.А., Кузнецов В.Б., Мартынов Е.В., Смирнов Э.Т. Экспериментальное и численное исследование акустических течений около объемных резонаторов // ПМТФ. 1997. Т. 38. № 6. С. 61-71.
6.Tkachenko L.A., Shaidullin L.R., Kabirov A.A. Acoustothermal Effect in an Open Tube with Section Leap for Nonlinear Gas Oscillations // Lobachevskii J. Math. 2020. V. 41. P. 1300–1304.
7.Gubaidullin D. A., Zaripov R. G., Tkachenko L. A., Shaidullin L. R. Deposition of polydisperse gas suspensions with nonlinear resonance oscillations in a closed tube // J. Acoust. Soc. Am. 2019. V. 145. № 1. EL30- EL33.
Линар Радикович Шайдуллин
ЦАГИ, МФТИ
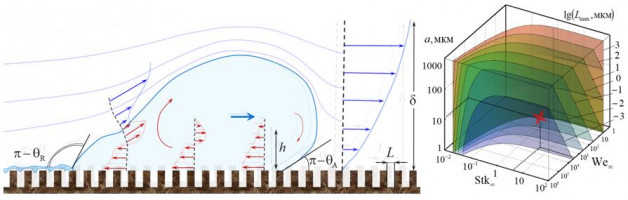
На основе разработанных математических моделей удара/отскока и скольжения переохлажденных капель по гидрофобной поверхности сформулированы безразмерные параметры и характеристики гидрофобных покрытий. Такие покрытия эффективно работают при малых значениях числа Вебера We = HρV2/σ для капель, взаимодействующих с поверхностью тела (H характерный период рельефа поверхности, здесь ρ – плотность жидкости, σ – коэффициент поверхностного натяжения, V – нормальная компонента скорости удара капли). Однако в случае динамического воздействия жидкости льдофобные свойства могут привести к обратным эффектам из-за проникновения жидкости в углубления и отвердевания в них. Гидрофобные свойства покрытий как правило определяются краевым углом смачивания θ и связанным с ним тензором эффективной длины скольжения , преобразовав который нетрудно получить выражение для граничного условия скольжения жидкости по гидрофобной поверхности. Наряду с описанными выше параметрами противообледенительное покрытие следует характеризовать параметром, учитывающим скорость соударения переохлажденных капель и напряжением сил адгезии образующегося при отвердевании капель льда. Другим управляющим параметром является доля первоначальной массы капли, оставшейся на поверхности после ее ударе . Кроме того, если нормальная компонента скорости удара переохлажденных капель о поверхность твердого тела меньше характерного зависящего от температуры значения капли останутся в жидком состоянии и будут двигаться по поверхности обтекаемого тела не замерзая. В работе получены выражения для сил, действующих на скользящие по поверхности капли с учетом их вращения и критерии переход от режима качения в режим скольжения в зависимости от интегрального момента аэродинамической силы в пограничном слое на поверхности.
Иван Алексеевич Амелюшкин
НИИ механики МГУ
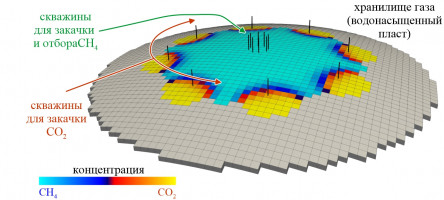
Расширена функциональность гидродинамического симулятора MUFITS для численного моделирования закачки многокомпонентных газов в водонасыщенные пласты. Расширение связано с развитием композиционного модуля симулятора, в котором парожидкостные равновесия многокомпонентных смесей рассчитываются с помощью кубического уравнения состояния [1]. В модуль встроена новая библиотека коэффициентов уравнения состояния для уточненного расчета растворимости CO2, N2, CH4, H2, O2, H2S и других углеводородных компонент в растворах соли. Для моделирования водных растворов используется подход, предполагающий использование различных и зависящих от солености коэффициентов парного взаимодействия для водной и газовой фаз [2]. Для уточненного моделирования растворимости газа и плотности жидкой фазы разработано несколько модификаций данного подхода [2].
Проведено тестирование разработанных алгоритмов в рамках расчета тестовых задач о закачке чистого сверхкритического CO2 в водонасыщенные пласты. Также проведены расчеты более сложных процессов, демонстрирующие потенциальные области приложения разработанного расширения симулятора. Во-первых, проведено моделирование закачки дымового газа, т.е. смеси воздуха и CO2, в водонасыщенный пласт. Показано, что даже небольшое количество воздуха (N2 и O2) в закачиваемом газе приводит к значительно более быстрому распространению газа по пласту. Во-вторых, проведено трехмерное моделирование закачки СО2 в подземные хранилища природного газа (ПХГ) с целью замещения буферного газа сверхкритическим СО2. Построена синтетическая 3-D модель ПХГ, в которой задано две группы скважин. Одна группа использовалась для закачки и отбора природного газа (CH4) с целью сглаживания сезонных колебаний спроса на природный газ. А вторая группа скважин, расположенная на периферии ПХГ, использовалась только для закачки сверхкритического CO2 на начальном этапе создания и эксплуатации ПХГ. Показано, что за счет циклического изменения направления фильтрации газов, вызванного закачкой и отбором CH4, более половины закачанного CO2 удается растворить в пластовой воде. При этом объем растворенного CO2 в несколько раз больше рабочего (активного) объема ПХГ. Проведено моделирование распространения CO2 в подземном хранилище в рамках расчета несколько сезонов закачки и отбора природного газа (CH4). Показано, что уже через 3 сезона эксплуатации ПХГ концентрация CO2 в отбираемом природном газе может превысить 4%, что снижает рентабельность предложенного подхода из-за необходимости сепарации CO2 от природного газа.
Исследование выполнено за счет гранта Российского научного фонда (проект № 19-71-10051).
1. Afanasyev A., Vedeneeva E. Compositional modeling of multicomponent gas injection into saline aquifers with the MUFITS simulator // 2021 J. Nat. Gas Sci. Eng. DOI: 10.1016/j.jngse.2021.103988
2. Søreide I., Whitson C.H. Peng-Robinson predictions for hydrocarbons, CO2, N2, and H2S with pure water and NaCl brine // 1992 Fluid Phase Equil. 77, 217–240.
Андрей Александрович Афанасьев
НИИ механики МГУ имени М.В. Ломоносова
При крупных взрывных извержениях часто наблюдаются электрические разряды в пепловой колонне, возникающие в результате электризации частиц пепла. Одной из основных причин электризации частиц является их трение и столкновение. Взаимодействие частиц существенно возрастает в сильно неоднородном течении. Причем существенное влияние на передачу и накопление заряда оказывает различие в размерах и свойствах частиц.
В этой работе разрабатывается модуль для расчета плоского нестационарного течения смеси газ – заряженные частицы с использованием построенной ранее модели их взаимодействия. При описании движения частиц используется подход Лагранжа: частицы движутся под действием силы тяжести, гидродинамических и электростатических сил; взаимодействуют друг с другом с изменением скоростей движения и зарядов. Предполагается, что движение частиц не влияет на течение несущей среды, поэтому течение несущей среды может быть рассчитано отдельно. Расчет проводится с использованием модельного нестационарного течения.
Наталья Владимировна Горохова
РГУ нефти и газа (НИУ) имени И.М. Губкина
Рисунок - Результативность воздействия на породу бинарными смесями.
Современные методы интенсификации и повышения добычи нефти из углеводородных пластов чаще всего основаны на действии тепловой энергии, поставляемой в горную породу извне. Прогрев насыщенной пористой среды приводит к увеличению нефтеотдачи за счет роста подвижности пластовых флюидов при снижении их вязкости и характера взаимодействия с пористой матрицей, а также за счет изменения пропускной способности пласта-коллектора при его раскольматировании, повышении трещиноватости и росте связанности пор. Наиболее эффективным является сочетание тепловых методов с использованием специальных химических веществ [1].
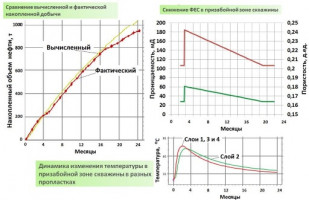
Настоящая работа посвящена термогазохимическому воздействию (ТГХВ) на призабойную зону скважины, где за счет экзотермической реакции разложения бинарной смеси (аммиачной селитры и нитрита натрия) в пористой среде аккумулируется выброс горячего газа и других продуктов реакции [2].
На основе результатов математического моделирования промысловых экспериментов [1,2] дано обоснование причин кратного продолжительного повышения дебита нефтяных скважин на низкопроницаемых пластах после проведения ТГХВ. Показано, что в отличие от классических тепловых методов воздействия на углеводородные пласты происходит не только снижение вязкости флюида, но и в ряде случаев включаются механизмы фазового преобразования различных углеводородных компонентов, в том числе изначально входящих в твердую часть породы.
Работа выполнена при поддержке гранта РФФИ №19-07-00433 А.
1. Kravchenko M.N., Dieva N.N., Fatykhov G.A. Hydrodynamic Analysis of Pyrolytic Studies for the Kerogen-Containing Rocks of Romashkinskoye Field. // Processes in GeoMedia 2021. Volume III. pp 273-284. https://doi.org/10.1007/978-3-030-69040-3_26
2. Lishcuk A. N., Kravchenko M. N., Shesternina N. V., Dieva N. N., Nafikov A. A., Khisametdinov M. R., Kataev A. V. (2020). The Results of Pilot and Industrial Application of Thermal-Gas-Chemical Well Treatment with Binary Mixtures and Development of Mathematical Models for Reservoir Processes in Source Oil Rock. // SPE Russian Petroleum Technology Conference. 2020, October 26. SPE-201812-RU. https://doi.org/10.2118/201812-MS
Нина Николаевна Диева
НИИ механики МГУ
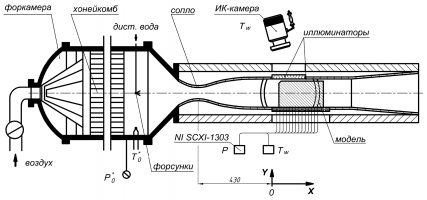
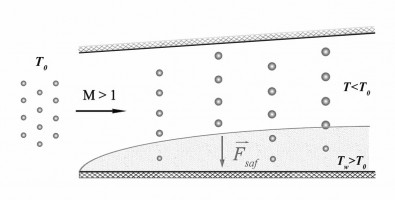
Исследованию взаимодействия многофазных потоков с обтекаемыми телами посвящено множество работ [1]. Наличие даже небольшого количества примеси (доли процента) в основном потоке может приводить к значительным изменениям параметров на поверхности обтекаемого тела. В данной работе внимание сконцентрировано на влиянии впрыска водных капель в форкамере аэродинамической установки на температуру поверхности модели, установленной в сверхзвуковой рабочей части. Охлаждение обтекаемой стенки в этом случае может позволить повысить эффективность методов тепловой защиты, устройств безмашинного энергоразделения и способов интенсификации теплообмена [2].
В работе представлены результаты сравнительного исследования обтекания плоской модели сверхзвуковым однофазным и двухфазным (газо-капельным) потоками. Экспериментальные исследования проводились на сверхзвуковом аэродинамическом стенде АР-2 (схема стенда представлена на рисунке) с использованием систем регистрации данных National Instruments, автоматизированных программ опроса и обработки показаний датчиков в среде LabView, термопар с термокомпенсацией, зондовых измерений, тепловизора, методов визуализации лазерным ножом и с помощью масло-сажевого покрытия.
Проведена серия экспериментальных измерений темпа охлаждения плоской модели и распределения температуры поверхности, обтекаемой сверхзвуковым газовым и газо-капельным потоками [3]. Числа Маха набегающего потока варьировались в диапазоне от 2.0 до 3.0. Относительный массовый расход жидкости (массовая концентрация) составлял до 0.5%. Жидкость (дистиллированная вода) распылялась через каскад центробежных форсунок мелкодисперсного распыла в воздушный поток в форкамере.
1.Вараксин А.Ю. Обтекание тел дисперсными газовыми потоками (обзор) // Теплофизика высоких температур. 2018. Т. 56. № 2. С. 282-305.
2.Leontiev A.I., Popovich S.S., Vinogradov U.A., Strongin M.M. Experimental research of supersonic aerodynamic cooling effect and its application for energy separation efficiency // Proceedings of the 16th International Heat Transfer Conference, IHTC-16. 2018. V. 212244. 8 p.
3.Попович С.С., Здитовец А.Г, Киселев Н.А., Виноградов Ю.А., Медвецкая Н.В. Измерение адиабатной температуры стенки плоской пластины, обтекаемой сверхзвуковым воздушно-капельным потоком // Известия Российской академии наук. Механика жидкости и газа. 2020. № 5.
Сергей Станиславович Попович
ИВМ СО РАН
В работе исследуется нестационарная сопряжённая начально-краевая задача, описывающая трёхмерное двухслойное осесимметрическое движение двух несмешивающихся вязких теплопроводных жидкостей в горизонтальном вращающемся цилиндре с твёрдой внешней стенкой и общей недеформируемой поверхностью раздела. При этом массовые силы отсутствуют. Рассматривается поле скоростей типа Хименца. Граница раздела обладает поверхностным натяжением, которое линейно зависит от температуры. Учитывается полное энергетическое условие на границе раздела. Как было показано в работах [1] в условиях высоких тепловых нагрузок, когда вязкость и теплопроводность обычных жидкостей существенно уменьшаются, а также для некоторых специальных рабочих жидкостей эффекты, связанные с изменениями энергии границы раздела, могут оказывать значительное влияние на динамику поверхностных явлений. С математической точки зрения, возникающая начально-краевая задача является нелинейной и обратной относительно градиентов давлений вдоль оси цилиндра. Для решения задачи применяется модифицированный метод Галёркина. В результате исследовано влияние физических и геометрических параметров системы на интенсивность возникающих течений. Стоит отметить, что полученное решение согласуется с результатами, полученными автором в работе [2], где рассматривалась стационарная задача о трёхмерном двухслойном осесимметрическом течении двух несмешивающихся вязких теплопроводных жидкостей в горизонтальном вращающемся цилиндре. Кроме того, получены точные решения сопряжённой задачи трёхмерной стационарной конвекции с учётом полного энергетического условия на поверхности раздела для ползущего течения.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (код проекта 20-01-00234) и Красноярского математического центра, финансируемым Минобрнауки РФ в рамках мероприятий по созданию и развитию региональных НОМЦ (Соглашение 075-02-2021-1384).
1. Torres F.E., Helborzheimer E. Temperature gradients and drag effects produced by convection of interfacial internal energy around bubbles // Phys. Fluids A. 1993. Т. 5. № 3. P. 537-549.
2. Magdenko E.P. Three-dimensional stationary flow of two immiscible liquids in a rotating cylinder with an isothermal interface // Journal "Interfacial Phenomena and Heat Transfer". 2020. Т. 8. № 4. P. 345-355.
Евгений Петрович Магденко
ИТПМ, НГУ
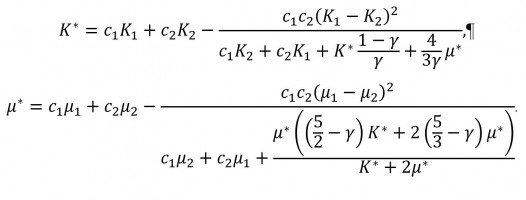
Одним из принципиальных нерешенных вопросов аналитического моделирования гетерогенных сред является учет микроструктуры системы (геометрии и физических свойств фаз). Введенной математической концепцией, направленной отобразить микроструктуру гетерогенной системы, выступает производная в обобщенном смысле [1]. Соответствующая производная содержит обычную и сингулярную составляющие. Сингулярная часть выражает разрывы поля на поверхности, что является естественным следствием анализа гетерогенной среды, характеризуемой развитой системой внутренних границ, разделяющих фазы с разными физическими свойствами. Проведение осреднения результата действия на поле производной в обобщенном смысле приводит к пространственной теореме осреднения в рамках теории смесей [2]. Описание гетерогенной среды осуществляется в рамках метода условных моментов [3]. Функционал данного подхода базируется на формализме функций Грина, условном осреднении и преобразовании Фурье. Методом условных моментов удается получить осредненные уравнения с эффективными коэффициентами упругости для среды в целом и для каждой фазы отдельно. Функция Грина, определяемая действующим оператором, отображает отклик поля в среде на приложенное воздействие. Исходя из этого ее роль в анализе характера распространения исследуемого поля по неоднородной системе является ключевой. В результате модификации операторов в исходной модели линейной теории упругости функция Грина характеризует микроструктурные особенности системы. Используя преобразованный в работе метод условных моментов, получены интегралы, содержащие осредненную функцию Грина и корреляционную функцию геометрии структуры. На основании этих членов микроструктура системы интегрально учтена во входящих в осредненные уравнения эффективных коэффициентах упругости.
1. Шварц Л. Математические методы для физических наук / Пер. с франц. М.: Мир, 1965.
2. Нигматуллин Р.И. – Основы механики гетерогенных сред // М. Наука., 1978.
3. Хорошун Л.П. О математической модели неоднородного деформирования композитов // Прикладная механика. 1996. №5 Том 32. С. 22-29.
2.
3.
Алексей Владимирович Мишин
НИИ механики МГУ, Москва
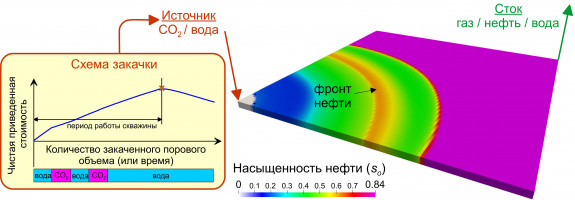
В докладе будет представлен метод ускоренной численной оптимизации закачки воды и СО2в нефтяные пласты. Оптимизация предполагает максимизацию чистой приведенной стоимости закачки путем сопряжения модели фильтрации с экономическими расчетами денежных потоков. Предлагаемый метод основан на построении иерархии композиционных моделей нефтяного пласта возрастающей сложности. В работе показано, что оптимальные безразмерные объемы воды и газа очень близки для одномерных и двумерных моделей водогазового воздействия на пласт, т.е. воздействия, предполагающего попеременную закачку воды и углекислого газа. Следовательно, решение задачи одномерной оптимизации дает хорошее приближение к решению двумерной задачи. В предлагаемом методе используется большее количество менее затратных одномерных расчетов фильтрации для того, чтобы получить хорошее начальное приближение для объемов закачки в гораздо более дорогостоящем двумерном моделировании. В численной оптимизации используются алгоритмы безградиентной оптимизации для грубых моделей на низких уровнях иерархии, чтобы гарантировать сходимость к глобальному максимуму чистой приведенной стоимости. Переключение на градиентные методы оптимизации происходит только на верхних уровнях иерархии. В данной работе приведены примеры применения алгоритма для оптимизации различных стратегий водогазового воздействия. Предполагается, что одномерное моделирование состава может быть эффективным для оптимизации площадных схем заводнения CO2. Показано, что при оптимизированном заводнении вода и CO2 появляются одновременно в добывающей скважине.
Анна Александровна Чернова
НИИ механики МГУ им. М.В. Ломоносова
Исследуется сверхзвуковое стационарное течение газокапельной смеси в плоском линейно расширяющемся канале с теплоизолированными стенками. Для анализа структуры течения и теплообмена используется двухконтинуальная модель газокапельной среды c пренебрежимо малой объемной концентрацией дисперсной фазы [1]. Учитываются фазовые переходы на поверхности капель. Предполагается, что во входном сечении канала фазы находятся в состоянии равновесия, а температура жидкости на поверхности и внутри капель не меняется во всей рассматриваемой области. Численно исследуется характер течения как в невязком ядре потока, так и в двухфазном пограничном слое.
Для определения параметров фаз вдали от стенки решаются квазиодномерные невязкие уравнения двухфазной среды с учетом обратного влияния и процесса конденсации. Показано, что температура газа вдоль оси канала меняется немонотонно: сначала температура снижается за счет падения давления в расширяющемся потоке, затем растет за счет конденсации. Разница температур фаз определяет скорость увеличения радиуса капель. Найдены условия, при которых происходит наиболее интенсивный рост капель.
Моделирование течения вблизи плоской стенки осуществляется с использованием уравнений ламинарного сжимаемого газокапельного пограничного слоя [2]. В пристеночной области помимо силы сопротивления Стокса учитывается боковая сила Сэфмана, приводящая к осаждению капель, в результате чего на поверхности стенки может формироваться тонкая пленка. В зависимости от свойств фаз и состояния потока во входном сечении канала возможны различные режимы обтекания стенки: полное отсутствие пленки, наличие пленки на конечном участке стенки, наличие непрерывной монотонно растущей пленки. Найдены диапазоны определяющих параметров, соответствующие каждому из режимов. Показано, что даже при массовой концентрации капель в набегающем потоке порядка 1% можно получить снижение температуры стенки в 1.5 раза и более. Полученные в данной работе количественные оценки снижения температуры стенки могут быть использованы при разработке систем безмашинного энергоразделения по методу Леонтьева [3].
Исследование выполнено по открытому плану МГУ за счет средств гранта Российского научного фонда (проект №19-19-00234).
Ирина Валерьевна Голубкина