Механико-математический факультет МГУ имени М.В. Ломоносова, Москва
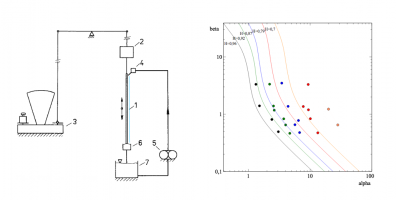
Толщина слоя со свободной поверхностью, стекающего по плоскости под действием силы тяжести определяется балансом массовой силы и трения на твердой поверхности. Для линейно-вязкой жидкости имеется точное решение уравнений Навье-Стокса, которое предсказывает, что расход жидкости пропорционален третьей степени толщины. При течении неньютоновской жидкости эта зависимость определяется реологическим законом, в частности, для степенной жидкости (эффективная вязкость является степенной функцией скорости сдвига) показатель степени зависит от показателя вязкости и расход пропорционален большей степени толщины для псевдопластических жидкостей и меньшей для дилатантных. В случае нелинейного закона зависимости вязкости от скорости сдвига колебания плоскости приводят к локальному изменению трения и существенному изменению расхода, причем его среднее значение по периоду также изменяется.
Изучается зависимость среднего расхода стекания неньютоновской жидкости по наклонной плоскости от параметров колебаний. Периодическое решение нелинейного уравнения в частных производных параболического типа разыскивается с помощью различных подходов. Рассмотрены асимптотические случаи: медленные колебания, период которых много больше времени вязкой релаксации, вызывающие квазистационарное течение; быстрые колебания, которые приводят к образованию тонкого осциллирующего подслоя; слабая зависимость вязкости от скорости сдвига. В первых двух случаях удается аналитически найти вид зависимости расхода от параметров колебаний. Для слабо неньютоновских жидкостей задача сводится к линейному неоднородному уравнению, периодическое решение которого находятся методом Фурье.
Для произвольного реологического закона и произвольных параметров колебаний решается нестационарная задача, периодическое решение устанавливается за достаточно большое время.
Результаты расчетов сравниваются с опубликованными экспериментальными данными. По осям отложены безразмерная амплитуда скорости плоскости и частота колебаний. Обнаружены значительные расхождения при малых амплитудах и частотах колебаний, различия, вероятно, связаны с недостаточно точно выбранной реологической моделью.
Работа выполнена при поддержке Совета по грантам при Президенте РФ (проект МК -1798.2017.1)
Регина Дамировна Вахитова
Механико-математический факультет, БГУ, г. Минск
В работе исследовано плоское движение тонких несмешивающихся слоев вязких жидкостей на внешней поверхности горизонтально расположенного, вращающегося с постоянной угловой скоростью цилиндра в поле сил тяжести и инерции. Подобного рода течения можно использовать при нанесении двухслойных покрытий на цилиндрические поверхности. Используя условие постоянства потока в окружном направлении [1], в работах [2,3] решена задача определения вида поверхностей двух слоев в случае установившегося движения жидкостей как на внутренней, так и на внешней поверхности вращающейся цилиндрической оболочки.
В данном исследовании получена общая трехмерная постановка задачи движения двух несмешивающихся слоев вязких жидкостей в поле центробежных, поверхностных и гравитационных сил.
С помощью основных постулатов теории тонкого слоя [4] система уравнений, представляющая собой постановку двумерной нестационарной плоской задачи, была упрощена. В случае умеренного движения, пренебрегая инерционными членами уравнений Навье-Стокса, получены окружные и радиальные компоненты скорости, а также взаимосвязанная система уравнений эволюции наружного и внешнего слоев в гравитационном и поверхностном поле. Разработан и реализован численный метод ее исследования. Получены и проанализированы формы раздела слоев и свободной поверхности от длительного устойчивого состояния при медленном вращении до развития возмущений со временем и распада слоя при увеличении влияния центробежных сил.
Александр Игоревич Ермоленко
БГУ
В работе исследовано плоское движение тонких несмешивающихся слоев вязких жидкостей на внешней поверхности горизонтально расположенного, вращающегося с постоянной угловой скоростью цилиндра в поле сил тяжести и инерции. Подобного рода течения можно использовать при нанесении двухслойных покрытий на цилиндрические поверхности. Используя условие постоянства потока в окружном направлении [1], в работах [2,3] решена задача определения вида поверхностей двух слоев в случае установившегося движения жидкостей как на внутренней, так и на внешней поверхности вращающейся цилиндрической оболочки.
В данном исследовании получена общая трехмерная постановка задачи движения двух несмешивающихся слоев вязких жидкостей в поле центробежных, поверхностных и гравитационных сил.
С помощью основных постулатов теории тонкого слоя [4] система уравнений, представляющая собой постановку двумерной нестационарной плоской задачи, была упрощена. В случае умеренного движения, пренебрегая инерционными членами уравнений Навье-Стокса, получены окружные и радиальные компоненты скорости, а также взаимосвязанная система уравнений эволюции наружного и внешнего слоев в гравитационном и поверхностном поле. Разработан и реализован численный метод ее исследования. Получены и проанализированы формы раздела слоев и свободной поверхности от длительного устойчивого состояния при медленном вращении до развития возмущений со временем и распада слоя при увеличении влияния центробежных сил.
Анастасия Геннадьевна Макоед
НИИ механики МГУ, Москва
Формирование порфировых месторождений цветных металлов связывают c образованием линз высококонцентрированных растворов соли [1]. При дегазации магматических очагов подобные линзы, содержащие в растворенном виде помимо соли также и цветные металлы, формируются на глубинах 1–2 км. Они находятся в условиях интенсивной конвекции воды, обусловленной высоким геотермическим градиентом, т.е. быстрым возрастанием температуры с глубиной. Если конвекция не размывает линзу, то создаются условия для формирования месторождения.
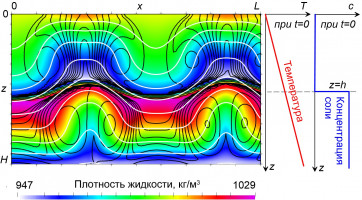
Для определения возможных условий существования линз рассмотрена нестационарная двухмерная задача фильтрации солёной жидкости в области (x,z)Î[0, L]´[0, H] (Рисунок), верхняя «открытая» граница которой z=0 соответствует поверхности Земли. На нижней границе z=H поддерживается повышенная температура (T), соответствующая заданному при t=0 линейному распределению T от z. При z<h концентрация соли (с) равна нулю, а при z³h она положительная константа. Предполагается, что плотность жидкости возрастает при уменьшении T или возрастании c. Таким образом, при t=0 имеется неустойчивая стратификации жидкости в областях z<h и z³h – плотность жидкости с глубиной z убывает, а при z=h плотность скачком возрастает.
В комплексе программ MUFITS [2] проведено прямое численное моделирование эволюции описанного распределения с учетом процессов теплопроводности, диффузии и механической дисперсии соли в пористой среде. Показано, что на начальном этапе развивается двухслойная конвекция с различными циркуляционными течениями в областях z<h и z³h [3], причем граница между жидкостями различной солености искривляется. Обнаружено два различных режима эволюции системы. При реализации первого режима конвективное течение полностью перемешивает жидкости различной солености, вынося соль через «открытую» границу z=0. Во втором режиме после начального переходного этапа, приводящего к незначительному перемешиванию жидкостей, система приходит к устойчивому положению равновесия, а конвекция прекращается. Причем, в области z³h сохраняются высокие значения концентрации. Первый и второй режимы определяют условия, при которых линза и месторождение не могут и, соответственно, могут образоваться.
Работа выполнена при финансовой поддержке РНФ (грант № 16-17-10199).
Рисунок: Распределение плотности жидкости; темными изолиниями показано распределение концентрации соли (с), а светлыми – температуры (T). Справа – начальные распределения T и c.
1. Afanasyev A., Blundy J., Melnik O., Sparks S. Formation of magmatic brine lenses via focused fluid-flow beneath volcanoes // Earth Planet. Sci. Lett. 2018. V.486. P.119–128.
2. Afanasyev A. MUFITS Reservoir Simulation Software. http://www.mufits.imec.msu.ru/
3. Griffiths R.W. Layered doubled convection in porous media // J. Fluid Mech. 1981. V.102. P.221–248.
Андрей Александрович Афанасьев
ЦАГИ имени проф. Н.Е. Жуковского, Жуковский, Моск. обл.
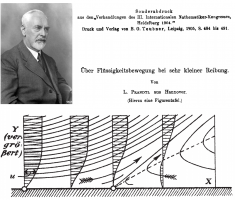
В докладе представлены исторические аспекты создания новых направлений в механике и в математике, связанные с новым подходом к исследованию проблем, содержащих малый параметр (или малые параметры). Эти подходы во многом связаны с именем Людвига Прандтля, создавшего как теорию пограничного слоя, так и методологию решения многих других задач с использованием асимптотических методов. Кроме истории создания этой теории представлены также и результаты, полученные в течение последующих 100 лет после публикации ключевой работы Прандтля. Обсуждаются перспективы дальнейших исследований, а также достигнутые результаты в области изучения устойчивости и перехода ламинарного пограничного слоя.
Рис. Сверху - Людвиг Прандтль и его труд «О движении жидкости с малым трением», 1904 г., снизу - пограничный слой на пластине (из работы Прандтля 1904 г.)
Игорь Иванович Липатов
МГУ им. М.В. Ломоносова
Рассматривается система уравнений одномерной мелкой воды над неровным дном. Для этой системы уравнений был найден новый закон сохранения, дополнительный к двум основным. Были также найдены все гидродинамические законы сохранения и симметрии для произвольных профилей дна. Система уравнений одномерной мелкой воды над наклонным дном связана точечным преобразованием с линейной системой уравнений, которая может быть получена из исходной формальным отбрасыванием нелинейных слагаемых. В данной работе рассматривается класс алгебраических точных решений линеаризованной системы уравнений одномерной мелкой воды над наклонным дном, который позволяет получить класс точных решений нелинейной мелкой воды с помощью этого преобразования. Описаны эффекты заплеска и усиления амплитуды при отражении волны от берега.
Константин Павлович Дружков
МГУ им. М.В. Ломоносова
Проблема дифракции ударной волны на клине, впервые описанная еще в XIX веке Махом, по сей день является не до конца изученной, несмотря на многочисленные экспериментальные, численные и теоретические исследования, проводимые в этой области. Самая полная на данный момент классификация различных автомодельных конфигураций регулярного и маховского отражения приведена в [1]. В зависимости от определяющих параметров задачи (числа Маха ударной волны, показателя адиабаты газа и угла клина) в расчетах и экспериментах [1] наблюдались различные конфигурации с ординарным, двойным и даже тройным маховским отражением.
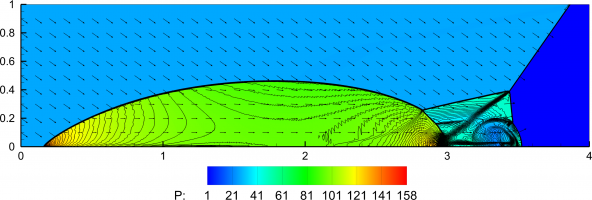
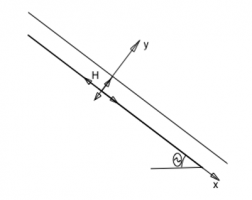
В настоящей работе исследованы конфигурации, характеризующиеся отрицательным углом наклона отраженного скачка [2] (скачок расположен ниже траектории движения тройной точки). Численные расчеты выполнены с использованием TVD модификации явной схемы МакКормака [3]. Расчетная область повернута так, что горизонтальная ось направлена вдоль образующей клина, а падающая ударная волна наклонена на угол клина (Рис. 1). В начальный момент ударная волна проходит через вершину клина, и параметры течения определяются соотношениями Рэнкина-Гюгонио на скачке. В процессе расчета поддерживаются граничные условия на левой и верхней границе, соответствующие движению ударной волны с известным числом Маха.
Обнаружен новый автомодельный режим многократного (четырехкратного) маховского отражения, характеризующийся ветвлением ударно-волновых конфигураций (Рис. 1). Для умеренных значений числа Маха режим реализуется в газах с показателем адиабаты близким к единице. Выполнение условия автомодельности проверялось сравнением распределений параметров в различные моменты времени. Проведено исследование перехода от нового режима отражения к регулярному отражению при изменении угла клина. Определены границы существования конфигураций многократного отражения при изменении показателя адиабаты газа.
Работа выполнена под руководством П.Ю. Георгиевского при частичной финансовой поддержке РФФИ (проект 18-01-00793-а).
Андрей Николаевич Максимов
Финансовый университет при Правительстве Российской Федерации (Краснодарский филиал)
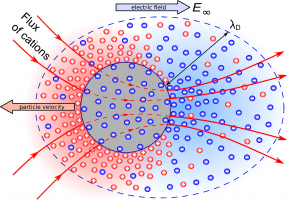
В докладе рассматривается задача движения заряженной микрочастицы с ионоселективной поверхностью в неограниченном объёме, заполненном раствором электролита, под воздействием внешнего электрического поля. В литературе рассмотрены аналогичные задачи для проводящих и диэлектрических частиц, в частных случаях выведены простые формулы типа формулы Гельмгольца-Смолуховского, описывающие зависимость скорости частицы от напряжённости поля. Экспериментально известно, что эта зависимость является линейной при слабых полях (равновесный электрофорез), а при увеличении напряжённости становится ближе к квадратичной (неравновесный электрофорез).
Для решения задачи применяется численное моделирование, которое для слабых и сильных полей дополняется асимптотическим анализом. Аналитически выводится упрощённая зависимость скорости частицы от напряжённости поля, которая отличается от формулы Гельмгольца-Смолуховского. Численно показывается смена режимов электрофореза (от равновесного к неравновесному) при увеличении напряжённости поля. Выводятся основные характеристики поведения электролита - распределения электрического потенциала, заряда и концентрации соли, а также поле скоростей в окрестности частицы. Полученные результаты качественно подтверждаются известными экспериментальными данными как для слабых, так и для умеренных полей. Для очень сильных полей в предложенной авторами модели проявляется разновидность электрокинетической неустойчивости, в результате чего решение с постоянной скоростью движения частицы перестаёт существовать.
В работе также оцениваются перспективы применения найденных режимов поведения частицы для решения технологических задач, описываемых в литературе: конструирования микронасосов, концентрирования и сепарации биологических объектов и т.п.
Работа выполнена в интересах проектов РФФИ (16-08-00643-а) и РНФ (17-79-10343).
Владимир Сергеевич Шелистов
БГУ
С целью изучения процессов центробежного литья металлов в работе исследовано неизотермическое плоское движение слоя вязкой жидкости на внутренней поверхности горизонтального вращающегося с постоянной угловой скоростью цилиндра в поле сил поверхностного натяжения, гравитации и инерции.
Решение изотермической задачи рассмотрено в [1-3]. Движение вязкой жидкости рассматривается в относительной полярной системе координат, связанной с вращающимся цилиндром, и описывается уравнениями Навье-Стокса с переменной вязкостью, энергии, неразрывности и неизвестной свободной поверхности. В уравнении энергии учтены конвективные составляющие и диссипативные члены. В случае достаточно быстрого вращения цилиндра получены уравнения первого приближения, подобные уравнениям пограничного слоя. Решения полученной системы ищется прямым методом с учетом граничных условий прилипания на поверхности цилиндра, отсутствия вязкого заимодействия с окружающей средой на свободной поверхности и теплообменом по условиям 3-его рода.
В результате исследований получена и численно решена система дифференциальных уравнений в частных производных определения эволюции свободной поверхности плоского слоя конечной толщины при умеренных и больших числах Рейнольдса Re в поле центробежных сил с учетом изменяющегося температурного поля в жидкости. Проведены сравнения с экспериментами и результатами исследования изотермической задачи. Учет нелинейного взаимодействия возмущений позволил проследить за механизмом эволюции поверхности слоя. Основной причиной распада слоя на внутренней цилиндрической вращающейся цилиндрической поверхности является гравитационная неустойчивость, вызванная значительным влиянием силы тяжести по сравнению с центробежными силами.
Анастасия Геннадьевна Макоед
Механико-математический факультет МГУ имени М.В. Ломоносова
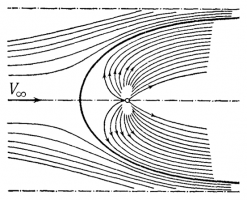
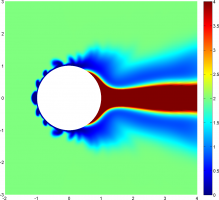
Известно, что при обтекании точечного источника (рис.1) с массовым расходом ρQ набегающим потоком со скоростью V, на источник будет действовать сила -ρQV. При движении сферической плавящейся частицы в собственном расплаве также необходимо учитывать изменение размеров частицы. Учет этих эффектов приводит к тому, что в уравнения движения частицы необходимо вводить реактивную силу, которая может существенно влиять на характер движения, как это было отмечено в [1] для случая идеальной жидкости. В работе [2] показано, что при наличии достаточно большого перепада температуры между частицей и расплавом данная сила может превышать силу вязкого сопротивления, что приводит к ускорению. частицы. Получен простой критерий, определяющий характер движения частицы в зависимости от относительного перепада температуры, числа Прандтля и относительной разности плотностей расплава и частицы.
На основании выведенных уравнений решается задача о случайном движении частицы, причём плавящейся за конечное время. Обнаружено, что среднеквадратичное отклонение такой частицы от начального положения за время плавления может быть даже неограниченно велико при больших перепадах температуры.
Уравнения движения частицы в вязком расплаве при отсутствии внешних сил допускают интеграл движения, учитывающий изменение кинетической энергии, который может быть использован при построении общей статистической теории плавящихся частиц. Решается уравнение Лиувилля для системы невзаимодействующих частиц и выводится выражение для давления как функции плотности сохраняющегося числа частиц и общей равновесной температуры расплава. В результате получена гиперболическая система уравнений движения континуума частиц на фоне механических и тепловых параметров расплава.
Для исследования особенностей движения континуума частиц решаются одномерные задачи с плоскими волнами: об однородном движении плавящихся частиц при нестационарном изменении температуры неподвижного расплава, а также о стационарном движении при постоянной температуре, проявляющая свойство запирания, связанное с невозможностью перехода через скорость звука, аналогичная газодинамической задаче о точечном источнике.
Работа частично поддержана грантом РФФИ № 17-01-00037.
1. А. Н. Голубятников. О взаимодействии плавящихся частиц о моделировании гравитации. // Вестник Нижегородского университета им. Н. И. Лобачевского, 2011. №4 (3). С. 728-729.
2. О. О. Иванов. К движению плавящейся частицы. // Вестник Московского университета. Сер. Математика. Механика, 2018 (в печати).
Олег Олегович Иванов
Финансовый университет при Правительстве Российской Федерации (Краснодарский филиал)
В докладе рассматривается задача движения заряженной микрочастицы с ионоселективной поверхностью в неограниченном объёме, заполненном раствором электролита, под воздействием внешнего электрического поля. Такое движение имеет перспективы применения в промышленности, биологии и медицине: для создания микронасосов, микросепараторов и других элементов миниатюрных приборов – "лабораторий на чипе". Исследование такого движения является достаточно сложной задачей из-за наличия эффектов, связанных как с электрофорезом (собственно движением частиц), так и с электроосмосом (движением среды). Наличие неустойчивостей, приводящих к вихреобразованию (которые характерны для электроосмотических течений), порождает интересные эффекты – например, интенсивное перемешивание – но одновременно снижает КПД электрофореза за счёт перераспределения подводимой энергии.
Численное моделирование задачи позволило выявить зависимость критического значения напряжённости внешнего поля, при котором движение электролита теряет устойчивость, от размеров микрочастицы. В отличие от схожей задачи об устойчивости течения в мембранной ячейке, эта зависимость не является монотонной и имеет максимум для частиц диаметром порядка 30 мкм. Неустойчивость приводит к стохастическому движению электролита, схожему с турбулентностью. Окрестность более крупных частиц оказывается подвержена неустойчивости целиком; для более мелких частиц зона неустойчивости сносится потоком и проявляется позади них. В последнем случае также отмечается нарушение монотонности зависимости скорости электрофореза от напряжённости поля вблизи критического значения последней.
Расчёты также показывают, что при большой напряжённости поля происходит накопление соли в узкой области за частицей. Неустойчивость практически не влияет на этот эффект.
Работа выполнена в интересах проектов РФФИ (16-08-00643-а) и РНФ (17-79-10343).
Владимир Сергеевич Шелистов
НИИ механики МГУ имени М.В. Ломоносова
Исследуется устойчивость уравнений Сен-Венана — уравнений, в гидравлическом приближении описывающих движение потоков в руслах и на склонах. Известно, что 1) малые мелкомасштабные возмущения в безграничном однородном потоке представляются в виде суммы двух волн, движущихся без изменения формы; 2) малые крупномасштабные возмущения распространяются в виде одной волны, движущейся без изменения формы; также известно 3) условие устойчивости по отношению к одномерным возмущениям [1].
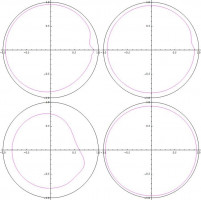
В данной работе устойчивость решений уравнений для потоков в руслах и на склонах изучается по отношению к двумерным возмущениям. Возмущения представляются в виде суммы синусоидальных волн с меняющейся во времени амплитудой. Получено дисперсионное уравнение, связывающее частоту и волновой вектор возмущений; исследование знаков корней дисперсионного уравнения проводится с применением принципа аргумента (см. Рисунок). Получен критерий устойчивости: возмущения не растут тогда и только тогда, когда для действительных значений частот 1) мнимая часть дисперсионного уравнения имеет два корня, 2) вещественная часть дисперсионного уравнения положительна при подстановке меньшего из корней мнимой части и отрицательна при подстановке большего. Получена форма критерия, где в явном виде представлены ограничения на параметры исследуемого потока. Рассмотрены частные случаи для значений параметров, дающих характеристики потоков, близкие к реальным.
Юлия Сергеевна Зайко
НИИ механики МГУ, Москва
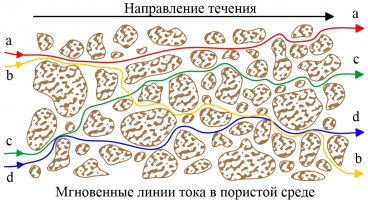
Многокомпонентные течения жидкостей и газов в пористых средах сопровождаются перемешиванием, приводящим к выравниванию полей концентрации – компонентного состава жидкости. К перешиванию приводит, во-первых, молекулярная диффузия, вызывающая перенос компонента жидкости в направлении противоположном градиенту его концентрации. Вторым механизмом перемешивания является механическая дисперсия в пористой среде, связанная с переменчивостью на масштабе отдельных пор поля скорости жидкости и соответствующим ветвлением траекторий движения элементарных частиц (Рис.) [1,2]. Интенсивность перемешивания из-за механической дисперсии зависит от направления и абсолютной величины средней скорости жидкости. В направлении, совпадающим с вектором средней скорости, интенсивность определяется различной скоростью движения частиц вдоль различных траекторий, а в перпендикулярном направлении – частотой ветвления траекторий. Во многих приложениях, как, например, при развитии слоистой конвекции в неизотермических фильтрационных течениях солёной воды, интенсивность перемешивания из-за механической дисперсии может на несколько порядков превышать интенсивность молекулярной диффузии.
В настоящей работе проведено расширение функциональных возможностей комплекса программ MUFITS [3] для численного моделирования неизотермических многокомпонентных многофазных течений в пористой среде. Разработан новый модуль для расчёта однофазной фильтрации с учётом механической дисперсий. Тестирование методов расчёта механической дисперсии, реализованных в модуле, проведено на одномерных и двухмерных задачах двухкомпонентной фильтрации соленой воды, допускающих аналитическое решение. Получены оценки для размеров шагов сетки по пространству и времени, при которых механическая дисперсия на порядок величины превосходит численную дисперсию. Обсуждаются особенности применения разработанного модуля к расчёту слоистой конвекции в пористой среде. Даны оценки скорости перемешивания из-за молекулярной диффузии и механической дисперсии при развитии конвекции.
Работа выполнена при финансовой поддержке РНФ (грант № 16-17-10199).
Рисунок: Схематическое изображение процесса механической дисперсии в пористой среде. В установившемся «осредненном» течении частицы жидкости, выпущенные в различные моменты времени из одно и той же точки (a/b; c/d), перемещаются вдоль различных траекторий.
1. Whitaker S. Diffusion and dispersion in porous media// AIChE J. 1967. V.13. P.420–427.
2.Sahimi M., et al. Dispersion in flow through porous media – I. One-phase flow// Chem. Eng. Sci. 1986. V.41(8). P.2103–2122.
3. Afanasyev A. MUFITS Reservoir Simulation Software. http://www.mufits.imec.msu.ru/
Андрей Александрович Афанасьев
Механико-математический факультет МГУ имени М.В. Ломоносова, Москва
В работе рассматривается течение слоя нелинейно-вязкой жидкости по вертикальной плоскости под действием силы тяжести. В этом случае имеется точное стационарное решение, описывающее течение с плоской границей раздела.
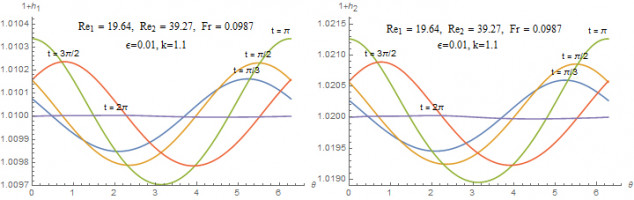
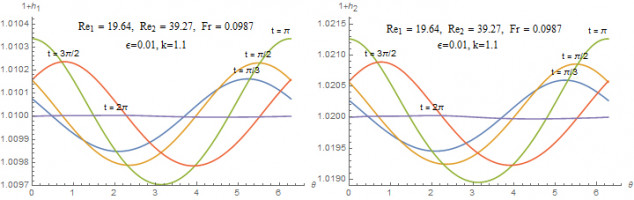
В настоящей работе рассматривается дополнительный фактор, влияющий как на параметры основного течения, так и на характеристики неустойчивости — осцилляции удерживающей поверхности. Предполагается, что плоскость совершает продольные колебания по гармоническому закону. При переходе в неинерциальную систему отсчета, связанную с плоскостью, возникает дополнительная массовая сила инерции, изменяющаяся со временем по гармоническому закону. Рассмотрено безволновое течение — плоскопараллельное течение с плоской границей раздела, в котором профиль продольной скорости периодически изменяется со временем с той же частотой, что и сила инерции. Показано, что средний расход псевдопластической жидкости растет с ростом амплитуды колебаний при фиксированной толщине слоя.
Выведено уравнение для описания длинных волн, частота которых много меньше частоты колебаний плоскости. Уравнение содержит не только средние по периоду колебаний плоскости характеристики, но и более высокие моменты, а именно среднее значение квадрата скорости. Таким образом, даже для случая ньютоновской жидкости, когда колебания не изменяют среднего расхода при заданной толщине, происходит изменение параметров волновой динамики.
Рассмотрена задача о линейной устойчивости безволнового решения. Показано, что наличие колебаний приводит к стабилизации пленки. Для случая быстрых колебаний, когда в пленке выделяется осциллирующий вместе с плоскостью тонкий подслой, результаты получены аналитически.
Работа выполнена при поддержке Совета по грантам при Президенте РФ (проект МК -1798.2017.1)
Регина Дамировна Вахитова