Центральный аэрогидродинамический институт им. проф. Н.Е. Жуковского (ЦАГИ)
Моделирование нестационарных дисперсных течений в неоднородных средах, и их взаимодействием с обтекаемым телом представляет большой научный и практический интерес в широком спектре областей науки и техники. Сложность строго математического моделирования стохастической динамики множества тел в градиентных средах и стохастический характер их траекторий в градиентных средах при экспериментальном исследовании продиктовали построение новых подходов в математическом и численном моделировании динамики таких течений. Кроме того, построена система уравнений стохастической динамики частиц естественного происхождения, которые имеют возможность самостоятельно перемещаться под действием градиента тепла, освещенности, поддерживать постоянную температуру и уклоняться от столкновений с препятствиями. Определены безразмерные управляющие параметры подобия таких течений. Развиты численные алгоритмы молекулярного моделирования управления взаимодействием дисперсных систем и реальных газов с поверхностью твердых тел, обладающих различной степенью гидрофобности. В частности, аналитически получены зависимости коэффициентов восстановления нормальных компонент скорости молекул от поверхности твердого тела в зависимости температуры Дебая, температуры и безразмерного параметра AK= εw-m/εm-m ≈ 0.5(1+cosθ), который можно трактовать как отношение энергий εw-m взаимодействия между молекулой потока и атомом поверхности к характерной энергии εm-m взаимодействия молекул потока между собой, θ – угол смачивания. Полученные решения существенно сокращают объем вычислительных ресурсов при расчете коэффициентов отскока частиц от поверхности твердых тел. Кроме того, в представленном исследовании получена статистическая диаграмма, показывающая вероятность кристаллизации переохлажденной метастабильной жидкости при различных количествах и интенсивности механических воздействий.
Иван Алексеевич Амелюшкин
ФГБОУ ВО УрГУПС
Рассматриваются двумерные изэнтропические течения в условиях действия силы тяжести. В качестве математической модели используется система уравнений газовой динамики. Для постановки задачи о распаде специального разрыва в системе делается вырожденная замена переменных, а именно: зависимые и независимые переменные меняются ролями [1]. В новых переменных для системы ставится начально-краевая задача с данными на звуковой характеристике и дополнительным условием. Доказывается теорема существования и единственности поставленной начально-краевой задачи в окрестности звуковой характеристики. Численно моделируется закон движения звуковой характеристики, отделяющей волну разрежения от неоднородного покоящегося газа.
Далее решение строится в виде степенных рядов. Для определения коэффициентов рядов выписываются и интегрируются системы обыкновенных дифференциальных уравнений. Анализ структуры коэффициентов рядов позволил доказать существование построенного решения в области от звуковой характеристики до границы газ-вакуум включительно. Для определения закона движения границы газ-вакуум выписывается квазилинейная система уравнений с частными производными, которая с помощью характеристического параметра сводится к системе обыкновенных дифференциальных уравнений. Численно моделируется закон движения свободной границы, отделяющей волну разрежения от вакуума.
Анна Сергеевна Кирьянова
Томский государственный университет
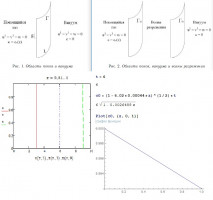
В настоящей работе численно решена задача искрового зажигания аэровзвеси порошка алюминия. Целью работы являлось определение критических условий зажигания порошка алюминия в зависимости от размера и массовой концентрации частиц. Постановка задачи основана на физико-математических постановках [1 – 2].
Математическая постановка задачи определяется системой уравнений, записанной в цилиндрической системе координат, и состоящей из уравнений неразрывности для газа, сохранения импульса и энергии для газа и частиц, баланса массы кислорода и частиц в смеси, уравнений счетной концентрации частиц и состояния газа. В уравнениях, определяющих математическую постановку задачи, правые части, отвечающие за химическое взаимодействие газа и частиц, определяются через радиус алюминия в частице, слагаемые, определяющие инерционное и тепловое взаимодействие определяются через радиус самой частицы, состоящей из алюминия и оксидного слоя. Радиус частицы и радиуса алюминия, оставшегося в частице после выгорания, определялись согласно [2].
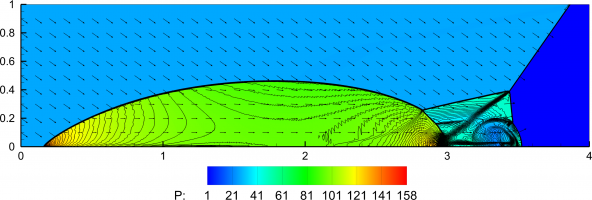
Задача решалась численно с использованием методов [3 – 4]. Метод решения и выбор расчетной сетки соответствовали работе [1]. В расчетах варьировались начальный радиус частиц алюминия и начальная массовая концентрация порошка на единицу объема. Из расчетов определялась минимальная энергия искры, необходимая для зажигания и дальнейшего распространения фронта горения по аэровзвеси. Пример полученных результатов расчета представлен на рис. 1.
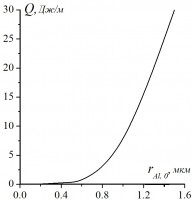
На рис. 1 представлена зависимость минимальной энергии искрового зажигания от начального размера частицы алюминия. Видно, что для радиуса частицы меньше 0.5 мкм минимальная энергия искрового зажигания стремится к одному и тому же значению.
В работе было выполнено исследование влияния массовой концентрации порошка на минимальную энергию искрового зажигания аэровзвеси алюминия. Получено, что увеличение массовой концентрации порошка приводит к уменьшению минимальной энергии искрового зажигания.
Исследование выполнено за счет гранта Российского научного фонда (проект №17-79-20011).
1.Моисеева К. М., Крайнов А. Ю. Численное моделирование искрового зажигания аэровзвеси угольной пыли// Физика горения и взрыва. 2018. Т. 54. № 2. С. 61–70.
2.Порязов В.А., Крайнов А.Ю., Крайнов Д.А. Математическое моделирование горения пороха Н с добавлением порошка алюминия// Инженерно-физический журнал. 2015. Т. 88. № 1. С. 93-101.
3.Годунов С.К., Забродин А.В., Иванов М.Я., Крайко А.Н., Прокопов Г.П. Численное решение многомерных задач газовой динамики. – М.: Наука, 1976.
4.Крайко А.Н. О поверхностях разрыва в среде, лишенной ‘собственного' давления// Прикладная математика и механика. 1979. Т. 43. № 3. С. 500-510.
Ксения Михайловна Моисеева
МГУ им. М.В. Ломоносова
Рассматривается система уравнений одномерной мелкой воды над неровным дном. Для этой системы уравнений был найден новый закон сохранения, дополнительный к двум основным. Были также найдены все гидродинамические законы сохранения и симметрии для произвольных профилей дна. Система уравнений одномерной мелкой воды над наклонным дном связана точечным преобразованием с линейной системой уравнений, которая может быть получена из исходной формальным отбрасыванием нелинейных слагаемых. В данной работе рассматривается класс алгебраических точных решений линеаризованной системы уравнений одномерной мелкой воды над наклонным дном, который позволяет получить класс точных решений нелинейной мелкой воды с помощью этого преобразования. Описаны эффекты заплеска и усиления амплитуды при отражении волны от берега.
Константин Павлович Дружков
Казанский (Приволжский) федеральный университет
Взвешенные в газе частицы представляют собой полидисперсную среду, описывающуюся функцией плотности распределения по фазовым переменным. В случае малых частиц функция плотности является одномерной и характеризуется распределением частиц по размерам. Для частиц крупных размеров дисперсная фаза имеет распределение и по другим переменным: компоненты скорости частиц и др.
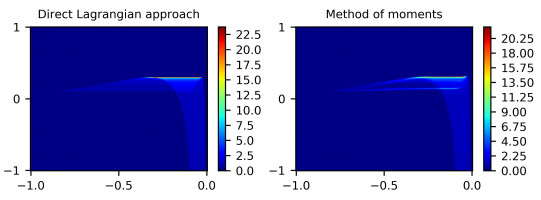
В настоящей работе развит метод условных моментов для моделирования дисперсной фазы, описываемой функцией распределения по двум компонентам скорости в предположении одинакового размера для всех частиц. Моделирование основано на численном решении уравнения Больцмана с учетом силы сопротивления по закону Стокса. Рассмотрены одно-, двух- и трехточечные аппроксимации функции плотности распределения в рамках ее дискретного представления с помощью квадратурных узлов. Модифицирована численная схема расчета адвекции инерционных частиц, гарантирующая физическое правдоподобие аппроксимации функции распределения при решении задачи ее восстановления по значениям моментов. Решена задача о течении инерционных частиц в гиперболическом потоке. Дано сравнение результатов моделирования, полученных методом моментов, прямым лагранжевым и полным лагранжевым подходами. Показано, что одноточечная аппроксимация функции распределения в зоне разворота частиц некорректно учитывает пересечение траекторий, приводящее к схлопыванию потока частиц в этой зоне. Двух- и трехточечные приближения верно отображают образование складки в зоне разворота. Показано, что наилучшее согласие с лагранжевыми подходами дает метод моментов с использованием двухточечной аппроксимации функции распределения. Решена задача о движении инерционных частиц в вихре Ламба. Показано, что метод моментов хорошо предсказывает положение фронта облака частиц, двигающегося от центра вихря, однако значительно занижает значение числовой плотности частиц на фронте.
Работа выполнена при поддержке Российского фонда фундаментальных исследований (проект № 18-31-00387).
Артур Камилевич Гильфанов
Федерального государственного бюджетного образовательного учреждения высшего образования «Комсомольский-на-Амуре государственный университет»

В последнее время в авиастроении в качестве деталей все больше применяются крупногабаритные монолитные и монолитно-сборные панели, которые позволяют повысить прочность и жесткость конструкций с одновременным снижением массы и улучшением аэродинамических характеристик. Задание аэродинамической формы таких монолитных панелей проводится процессами формообразования, осуществляющихся в режимах пластического деформирования, как при обычных, так и при повышенных температурах [1]. Формирование в режиме ползучести и при напряжениях, не превышающих предела упругости материала, обеспечивает более высокий остаточный прочностной ресурс по сравнению с методом обычной холодной штамповки [2]. Экспериментальные результаты позволяют отождествить работу рассеяния с параметром поврежденности [2]. В этом случае процессы формообразования позволяют управлять уровнем поврежденности материала, согласовывать с технологическими ограничениями, за счет оптимального выбора пути деформирования во времени [3].
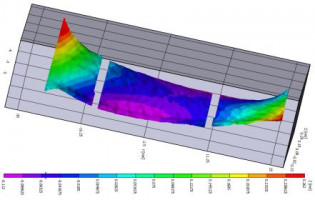
В качестве примера, рассматривается формование изделий из листов и панелей, с помощью реконфигурируемого стержневого пуансона (матрицы), позволяющего изменять форму заготовки. Точность формы и качество детали, полученной технологиями обработки материалов давлением при заданных параметрах процесса, зависит от точности вычисленной формы оснастки с законом изменения в процессе деформирования, задающей упреждающую форму (рис.1.). Упреждающая форма должна обеспечивать заданную остаточную кривизну панели после освобождения ее от силовой оснастки.
Задача деформирования в ползучести c контактными условиями решается методом конечных элементов. В качестве критерия оптимизации принимается накопленная в процессе деформирования работа рассеяния. Учитывая дискретные по времени уравнения пошаговой процедуры интегрирования и минимизируемую функцию, формулируется дискретная задача оптимального управления. Данная задача решается методом динамического программирования.
Таким образом, разработанный численный метод позволяет находить рациональные процессы формообразования не только для идеальной пластинки или оболочки, но и для таких деталей, как панели крыла.
Работа выполнена при финансовой поддержке РФФИ (16-31-60038 мол_а_дк), совета по грантам Президента РФ (МД-4117.2018.1).
1. Аннин Б.Д., Олейников А.И., Бормотин К.С. Моделирование процессов формообразования панелей крыла самолета SSJ-100 // Прикладная механика и техническая физика. 2010. Т.51. №4. С. 155-165.
2. Соснин О.В., Никитенко А.Ф., Горев Б.В. К обоснованию энергетического варианта теории ползучести и длительной прочности металлов // Прикладная механика и техническая физика. 2010. 51. № 4. 188–197.
3. Бормотин К.С., Олейников А.И. Вариационные принципы и оптимальные решения обратных задач изгиба пластин при ползучести // Прикладная механика и техническая физика. 2012. № 5. 136–146.
Константин Сергеевич Бормотин
ФГБОУ ВО Российский экономический университет им. Г. В. Плеханова, ФГБУН Институт биохимической физики им. Н. М. Эмануэля

Огромные масштабы промышленного производства и обширный спектр применения полиэтилена свидетельствуют о важности разработки новых материалов на его основе. В настоящей работе в качестве добавки к полиэтилену низкой прочности (ПЭ) использовали натуральный каучук (НК) – продукт растительного происхождения, достаточно быстро подвергающийся окислительной и биологической деструкции, введение которой способствует ускорению процесса биодеградации ПЭ. Объектами исследования являлись двойные композиты на основе ПЭ (TM 15803-020, ОАО «Нефтехимсевилен») с содержанием 10-50 мас.% НК (TM SVR 3L, Вьетнам). Смешение полимеров на смесителе типа Брабендер при 140±5°С и 30 об./мин с последующим прессованием при 140±5°С и быстрым охлаждением до 20±2°С. Механические свойства композиций при растяжении исследовали с использованием разрывной машины DVT Devotrans™ GP UG 5 DLC-0,5 в соответствии с ISO 527-3:1996 (форма образца тип 2, скорость растяжения 100 мм/мин).
По результатам испытаний установлено, что соотношение ПЭ/НК сильно влияет на относительное удлинение (Ɛр) и прочность при разрыве (σр), а также модуль упругости (Eупр). Наблюдается значительное снижение σр при добавлении 10 и 20 мас.% НК по сравнению с чистым ПЭ. Неоднородная система, образованная путем добавления НК к ПЭ, способствует распространению трещин и уменьшению σр. При деформации смеси, чем больше размер диспергированных доменов, тем выше перенапряжение, происходящее на границе раздела фаз. Ɛр резко уменьшается при добавлении 10 мас.% НК. Это связано с образованием гетерогенной системы, где домены НК ведут себя как дефектные структуры в матрице ПЭ. Когда НК образует непрерывную фазу (более 20 мас.% НК) Ɛр возрастает. Материалы становятся более гибкими, о чем свидетельствует уменьшение Eупр пропорционально содержанию НК в смеси.
Иветта Арамовна Варьян
Национальный исследовательский ядерный университет "МИФИ"
Выполнение механических испытаний материалов регламентируется ГОСТами, в которых прописаны требования к образцам, испытательному оборудованию, условиям проведения испытаний и способам обработки результатов [1–4].
Использование метода цифровой корреляции изображений при проведении механических испытаний позволяет успешно осуществлять контроль всех этапов механических испытаний.
С применением метода цифровой корреляции изображений возможно определение качества поверхности, геометрии и формы испытуемых образцов, контроль процесса установки образца в захваты испытательной машины, а также положения губок захватов в пространстве.
Разработана методика определения модуля упругости и коэффициента Пуассона с использованием функции оптического экстензометра. Сравнение значений модуля упругости, полученных с помощью оптического экстензометра, и значений, полученных с внешнего экстензометра, практически совпадают.
Лидия Александровна Дегадникова
МГУ им. М.В. Ломоносова
Проблема дифракции ударной волны на клине, впервые описанная еще в XIX веке Махом, по сей день является не до конца изученной, несмотря на многочисленные экспериментальные, численные и теоретические исследования, проводимые в этой области. Самая полная на данный момент классификация различных автомодельных конфигураций регулярного и маховского отражения приведена в [1]. В зависимости от определяющих параметров задачи (числа Маха ударной волны, показателя адиабаты газа и угла клина) в расчетах и экспериментах [1] наблюдались различные конфигурации с ординарным, двойным и даже тройным маховским отражением.
В настоящей работе исследованы конфигурации, характеризующиеся отрицательным углом наклона отраженного скачка [2] (скачок расположен ниже траектории движения тройной точки). Численные расчеты выполнены с использованием TVD модификации явной схемы МакКормака [3]. Расчетная область повернута так, что горизонтальная ось направлена вдоль образующей клина, а падающая ударная волна наклонена на угол клина (Рис. 1). В начальный момент ударная волна проходит через вершину клина, и параметры течения определяются соотношениями Рэнкина-Гюгонио на скачке. В процессе расчета поддерживаются граничные условия на левой и верхней границе, соответствующие движению ударной волны с известным числом Маха.
Обнаружен новый автомодельный режим многократного (четырехкратного) маховского отражения, характеризующийся ветвлением ударно-волновых конфигураций (Рис. 1). Для умеренных значений числа Маха режим реализуется в газах с показателем адиабаты близким к единице. Выполнение условия автомодельности проверялось сравнением распределений параметров в различные моменты времени. Проведено исследование перехода от нового режима отражения к регулярному отражению при изменении угла клина. Определены границы существования конфигураций многократного отражения при изменении показателя адиабаты газа.
Работа выполнена под руководством П.Ю. Георгиевского при частичной финансовой поддержке РФФИ (проект 18-01-00793-а).
Андрей Николаевич Максимов
ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Нарушение легочного кровообращения – это сопутствующая патология при врожденных пороках сердца у детей (отсутствие межжелудочковой перегородки, тетрада Фалло, коарктация (сужение) аорты). Частота встречаемости врожденных пороков сердца в России возросла до 15 на 1000 родившихся живыми. По данным ВОЗ детская смертность от сердечно-сосудистых заболеваний в возрасте 0–4 лет в России ежегодно составляет около 8000 человек. Врожденные пороки сердца у детей нарушают в первую очередь кровоснабжение легких, что ведет к неравномерному их росту и недостаточному насыщению крови кислородом. Оперативное вмешательство по устранению врожденных пороков сердца может проводиться уже на третьи сутки после рождения ребенка [1]. Решение о схеме оперативного лечения, принимается, как правило, экспертным путем, что несет некоторую субъективность оценки.
Существует несколько сценариев оперативного вмешательства, которые позволяют перераспределить кровоток. Одним из наиболее распространенных методов устранения патологических изменений является использование модифицированного Блелок-Таусиг шунтирования (системно-легочный анастомоз). Для объективизации этой процедуры необходимо применить методы биомеханического моделирования, в результате чего можно судить о степени восстановления нормального кровоснабжения.
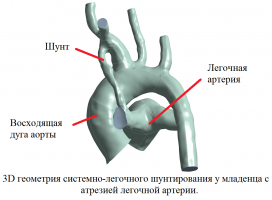
На основе изображений, полученных из МСКТ (мультиспиральная компьютерная томография) с контрастом, была построена индивидуализированная биомеханическая модель системы «аорта–легочная артерия-шунт» для анализа гемодинамики в данной области.
Проведено гидродинамическое исследование кровообращения у ребенка (возраст 9 дней) с врожденным пороком сердца (атрезия легочной артерии) после оперативного лечения с использованием системно-легочного шунтирования. Получены основные гемодинамические параметры (скорость, давление, расход, Qs/Qp,OSI, WSS, TAWSS и т.д.), которые позволяют проанализировать эффективность оперативного вмешательства.
1.Синельников Ю.С., Орехова Е.Н., Шехмаметьев Р.М., Породиков А.А., Комарова Е.В., Зинченко А.А., Рамалданов К.Р. Случай успешной радикальной коррекции тетрады Фалло с аномальной передней нисходящей артерией, отходящей от правой коронарной артерии // Детские болезни сердца и сосудов. 2016; Т. 13. №. С. 243-248.
Марина Ивановна Шмурак
Национальный исследовательский Томский государственный университет
В работе проведено численное моделирование естественной конвекции в частично пористой полости с использованием неравновесной тепловой модели. Рассматривается замкнутая квадратная полость, содержащая пористую вставку высоты h и теплогенерирующий теплопроводный источник энергии на нижней стенке. Горизонтальные стенки области теплоизолированы, боковые поддерживаются при постоянной температуре охлаждения. Область заполнена ньютоновской теплопроводной жидкостью, удовлетворяющей приближению Буссинеска. Вязкость рабочей среды зависит от температуры по экспоненциальному закону [1]. Считается, что температура пористой вставки отлична от температуры жидкости, и моделирование ведется в рамках тепловой локально-неравновесной модели. Для описания пористого изотропного слоя используется модель Дарси-Бринкмана.
Уравнения, описывающие теплоперенос в рассматриваемой области, решались в безразмерных преобразованных переменных «функция тока – завихренность – температура». На границах раздела сред (чистая среда/пористая среда, пористая среда/источник энергии) реализованы граничные условия четвертого рода.
Полученные результаты позволяют прогнозировать поведение пассивных охлаждающих систем для электронных устройств различного типа в первом приближении. Благодаря фундаментальному характеру исследования и широкому диапазону определяющих параметров рассмотрены различные варианты взаимодействия жидкой и пористой среды, рабочих сред, а также мощностей тепловыделителя. Установлены основные зависимости между выбранными параметрами и эффективностью теплоотвода от источника.
Работа выполнена при финансовой поддержке Российского научного фонда (проект № 17-79-20141).
1. Astanina M. S., Sheremet M. A., Umavathi J. C. Unsteady natural convection with temperature-dependent viscosity in a square cavity filled with a porous medium // Transport in Porous Media. – 2015. – Vol.110 – No. 1. – P. 113–126
Марина Сергеевна Астанина
Финансовый университет при Правительстве Российской Федерации (Краснодарский филиал)
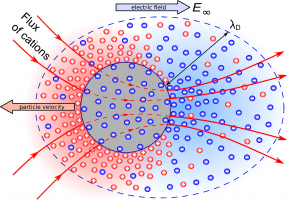
В докладе рассматривается задача движения заряженной микрочастицы с ионоселективной поверхностью в неограниченном объёме, заполненном раствором электролита, под воздействием внешнего электрического поля. В литературе рассмотрены аналогичные задачи для проводящих и диэлектрических частиц, в частных случаях выведены простые формулы типа формулы Гельмгольца-Смолуховского, описывающие зависимость скорости частицы от напряжённости поля. Экспериментально известно, что эта зависимость является линейной при слабых полях (равновесный электрофорез), а при увеличении напряжённости становится ближе к квадратичной (неравновесный электрофорез).
Для решения задачи применяется численное моделирование, которое для слабых и сильных полей дополняется асимптотическим анализом. Аналитически выводится упрощённая зависимость скорости частицы от напряжённости поля, которая отличается от формулы Гельмгольца-Смолуховского. Численно показывается смена режимов электрофореза (от равновесного к неравновесному) при увеличении напряжённости поля. Выводятся основные характеристики поведения электролита - распределения электрического потенциала, заряда и концентрации соли, а также поле скоростей в окрестности частицы. Полученные результаты качественно подтверждаются известными экспериментальными данными как для слабых, так и для умеренных полей. Для очень сильных полей в предложенной авторами модели проявляется разновидность электрокинетической неустойчивости, в результате чего решение с постоянной скоростью движения частицы перестаёт существовать.
В работе также оцениваются перспективы применения найденных режимов поведения частицы для решения технологических задач, описываемых в литературе: конструирования микронасосов, концентрирования и сепарации биологических объектов и т.п.
Работа выполнена в интересах проектов РФФИ (16-08-00643-а) и РНФ (17-79-10343).
Владимир Сергеевич Шелистов
НИИ механики МГУ имени М.В. Ломоносова
Молнии, образующиеся в пепловой колонне – довольно частое явление, происходящее во время крупных эксплозивных извержений. Вулканические молнии образуются в процессе электризации и пространственного разделения разноимённо заряженных частиц пепла при достижении некоторой критической разности потенциалов. Предполагается, что электризация частиц происходит за счёт трения и столкновения частиц [1].
В работе рассматривается течение однородного потока газа с частицами, имеющими разные диаметры (100 и 500 мкм) и заряды. Для моделирования движения частиц в потоке газа используется лагранжев подход. Учитывается взаимодействие заряженных частиц и возможность их столкновения и передачи электрического заряда. Проводится исследование влияния различных параметров: концентрации частиц в смеси, доли крупных частиц, начальных зарядов частиц.
В результате исследования показано, что при достаточно высоких концентрациях необходимо учитывать столкновение частиц. Получено, что частицы могут приобрести существенный заряд (при нулевых начальных зарядах) только за счёт их столкновений.
Работа выполнена при поддержке гранта РФФИ 16-05-00004 А
1. Горохова Н. В. Формирование вулканических молний в пепловой колонне // Всероссийская конференция молодых-ученых механиков, 5 - 15 сентября 2017 г., Сочи, "Буревестник" МГУ, Тезисы докладов. 2017.
Наталья Владимировна Горохова
БГУ, Минск
Струйные течения жидкости встречаются в различных технологических процессах. Так, процесс производства минеральной ваты дутьевым способом состоит в разрушении струи минерального расплава высокоскоростным газовым потоком со скоростью около
200 м/с. Чтобы увеличить интенсивность распада струй, предлагается повышать внешнее давление.
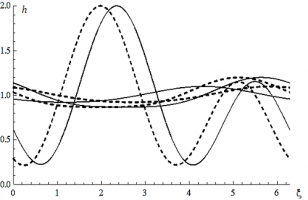
Теории струйных течений посвящено достаточно большое количество работ [1,2]. В книге [3] отражены исследования устойчивости капиллярных струй в линейном приближении, а также в нелинейном случае без учета внешнего воздействия. В данном исследовании рассматривается нелинейное развитие осесимметричных капиллярных волн, возникающих в струе жидкости при наличии переменного по времени внешнего давления после потери устойчивости. Исследования течения проводится на основе приближения пограничного слоя в случае достаточно длинных волн, когда составляющие скорости зависят только от осевой координаты. Это позволяет перейти к изучению невязкого струйного течения. Решение полученной системы в относительной движущейся с фазовой скоростью волны системе координат ищется в виде разложения в ряд Фурье с членами до второго порядка включительно. Выведенные эволюционные уравнения исследуются численно методом Рунге-Кутта с постоянным шагом по времени при различных начальных возмущениях.
Наиболее неустойчивыми являются длинноволновые возмущения с 0 < α < αопт, где αопт = 0.7, что примерно соответствует максимально растущим возмущениям по линейной теории устойчивости. При начальных значениях времени и модах с 0 < α < αопт возмущения достаточно малы, и форма поверхности близка к гармонической. С ростом времени становится заметна роль второй гармоники на развитие возмущений. Колебания становятся нелинейными и видно образование второго максимума на длине волны. Наличие второго максимума поверхности определяет возможность образования капель разного размера, что наблюдается в действительности при распаде струй. С учетом полученных результатов можно сделать вывод о том, что с увеличением влияния внешнего давления время распада струи на капли, когда в ней появляются перетяжки, уменьшается, и возмущения развиваются более интенсивно. При волновых числах с αопт < α < 1 с ростом времени возмущения возрастают, но форма поверхности остается близка к гармонической. Если α > 1, то течение становится устойчивым. С увеличением начального возмущения поверхности струи время распада уменьшается.
В результате исследований определены области неустойчивых возмущений, форма поверхности струи, продольная и радиальная составляющие скорости течения. Найдено время распада в зависимости от начальных возмущений поверхности и волнового числа. Следует отметить, что определение формы слоя позволяет вычислить ускорения точек поверхности, которые используются в формуле расчета диаметра струй при дутьевом способе образования минеральных волокон [4,5].
ЛИТЕРАТУРА
1. Шкадов В.Я., Маркова М.М. Нелинейное развитие капиллярных волн в струе жидкости // Изв. АН СССР, МЖГ,1972, №3, с.30-37.
2. Чесноков Ю.Г. Нелинейное развитие капиллярных волн в струе вязкой жидкости //Журнал технической физики, 2000, т.70, вып.8, с.31-38.
3. Шкадов В.Я. Некоторые методы и задачи теории гидродинамической устойчивости // Ин-т механики МГУ. Научн. тр.- М., 1973. Вып. 25. - 192 с.
4. Кулаго А.Е., Конон П.Н. Определение ускорений точек поверхности возмущенной струи Сб. трудов ВНИПИ Теплопроект «Конструкция и строительство специальных сооружений».-М.,1983.- C. 39-48.
5. Конон П.Н., Макоед А.Г. Исследования струйных течений жидкости с учетом внешнего воздействия// Международный научно-технический журнал «Теоретическая и прикладная механика». Минск -2018.- Вып. 33. - С.426-429.
Анастасия Геннадьевна Макоед
Московский авиационный институт (национальный исследовательский университет)
Существует ряд подходов к созданию математических моделей механики сплошных сред. Одним из перспективных направлений, дающих возможность наиболее точно аналитически описать поведение среды, является моделирование связанных полей различной природы, примером которого является модель термоупругости с учётом диффузии. Она позволяет описать взаимное влияние поля перемещений и поля температур, учитывая при этом изменение поля концентраций материи в деформируемом твёрдом теле. Большинство имеющихся моделей термоупругости с учётом диффузии представлены в стационарной или квазистационарной постановке и не учитывают перекрестных диффузионных эффектов. Для решения этих задач используются в основном численные алгоритмы, однако для моделирования и анализа сложных реальных процессов часто требуется именно нестационарная аналитическая модель.
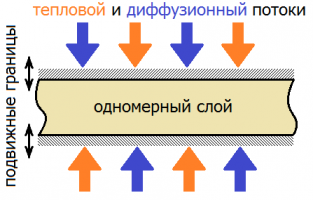
В работе рассматривается связанная одномерная нестационарная задача термоупругости с учётом массопереноса для однородной многокомпонентной среды (слой или полупространство). Математическая постановка задачи в прямоугольной декартовой системе координат представляет собой связанную систему уравнений в частных производных, состоящую из уравнений движения, теплопереноса и N уравнений массопереноса (N – число компонент среды). Уравнения массопереноса также учитывают взаимное влияние полей концентраций различных компонент среды. На границах среды задаются перемещение, тепловой поток и диффузионные потоки для каждой компоненты среды, зависящие от времени. В случае полупространства один наборов граничных условий заменяется на условие ограниченности искомых величин на бесконечности. Начальные условия приняты нулевыми.
Решение ищется в интегральной форме, которая представляет собой свёртку по времени функций Грина с правыми частями граничных условий. В задаче для слоя, для нахождения функций Грина, используется преобразование Лапласа по времени и разложение искомых функций в неполные ряды Фурье, что сводит задачу в изображениях к системе линейных алгебраических уравнений относительно искомых функций. В задаче для полупространства вместо разложения в ряды Фурье используется синус˗, косинус˗преобразование Фурье. При таком подходе трансформанты искомых функций являются рациональными функциями параметра преобразования Лапласа. Их оригиналы находятся с помощью известных теорем операционного исчисления.
Работа выполнена при финансовой поддержке РФФИ (проекты №17-08-00663 и №18-31-00437).
1. Давыдов С.А., Земсков А.В., Тарлаковский Д.В. Двухкомпонентное упруго диффузионное полупространство под действием нестационарных возмущений // Экологический вестник научных центров Черноморского Экономического сотрудничества. – 2014. – № 2. – С. 31–38.
2. Давыдов С.А., Земсков А.В., Тарлаковский Д.В. Поверхностные функции Грина в нестационарных задачах термомеханодиффузии // Проблемы прочности и пластичности. – 2017. – Т.79, № 1. – С. 38–47.
Сергей Андреевич Давыдов