Санкт-Петербургский политехнический университет Петра Великого
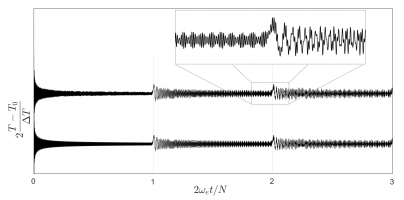
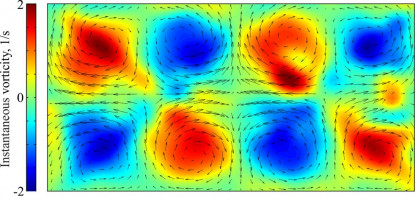
Описание неравновесных тепловых процессов в системах с конечным числом частиц представляет особый научный и практический интерес, особенно благодаря активному развитию нанотехнологий [1]. Ранее было показано, что в случае мгновенного нагрева одномерного гармонического кристалла реализуются затухающие колебания кинетической температуры [2, 3]. В настоящей работе исследуется аналогичные процессы для одномерного гармонического кристалла с конечным числом частиц. Построено аналитическое решение, описывающее нестационарный тепловой процесс в системе. В работе показано, что через определённое время в конечном кристалле реализуется резкое увеличение амплитуды колебаний кинетической температуры (тепловое эхо).
Данное явление происходит периодически, с периодом, который зависит от размера кристалла, и каждое последующее тепловое эхо слабее предыдущего. Аналитически получено, что изменение кинетической температуры описывается бесконечной суммой функций Бесселя с кратными индексами, а тепловое эхо в термодинамическом пределе описывается функцией Эйри [4]. Найден новый интеграл движения, связывающий обобщённые температуры.
Показано, что в конечном кристалле дисперсия смещений, в среднем, возрастает в соответствии с параболическим законом до величины, пропорциональной числу частиц в кристалле, а затем уменьшается до почти нулевого значения. Таким образом, кристалл возвращается к состоянию, близкому к исходному состоянию. Чем больше частиц находится в кристалле, тем более выраженным является эффект возврата. Представлен аналитический анализ описанных выше явлений [4].
Список литературы:
[1] Кривцов А. М., Морозов Н. Ф. О механических характеристиках наноразмерных объектов. Физика твердого тела. 2002. Т. 44. №12. С. 2158–2163
[2] Кривцов А. М. Колебания энергий в одномерном кристалле. Доклады академии наук. 2014. том 458, №3, C. 279–281.
[3] Кривцов А. М. Распространение тепла в бесконечном одномерном гармоническом кристалле. Доклады академии наук. 2015. Т. 464, №2, C. 162–166.
[4] А. М. Кривцов, А. С. Мурачёв, Д. В. Цветков. Нестационарные термо-диффузионные процессы в конечном одномерном кристалле. Чебышевский сб., 2018, 18:3
Андрей Сергеевич Мурачёв
Московский авиационный институт(национальный исследовательский университет), НИИ механики МГУ имени М.В. Ломоносова
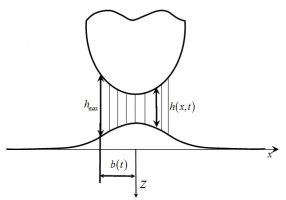
Рассматривается нестационарное взаимодействие жесткого выпуклого штампа с упругой изотропной полуплоскостью при учете межмолекулярного адгезионного поверхностного притяжения. Учет адгезионного притяжения в нестационарных контактных задачах очень важен в случаях, если материал контактирующих тел имеет небольшую плотность и сравнительно небольшие размеры.
В представленной работе межмолекулярное адгезионное притяжение описывается с помощью известной модели Можи [1]. Согласной данной модели, если зазор между двумя соседними поверхностями меньше некоторого критического значения, то на поверхности тел действует постоянная сила адгезионного притяжения. При этом, в зоне контакта двух тел сила адгезионного притяжения отсутствует.
Имея ввиду особенность модели Можи, взаимодействие жесткого штампа с упругой полуплоскостью можно разбить на два различных этапа:
1) Штамп и упругая полуплоскость не контактируют, но на их поверхности действует сила адгезионного притяжения (см. рис.).
2) Штамп находится в контакте с упругой полуплоскостью, на данном этапе необходим учет как контактных напряжений, так и сил адгезионного притяжения.
В рамках первого этапа взаимодействия, была поставлена следующая задача: в начальный момент времени минимальное расстояние между штампом и упругой полуплоскостью равно критическому значению зазора, при котором начинают действовать силы адгезинного притяжения. По мере движения штампа по некоторому известному закону на встречу упругой полуплоскости, носитель адгезионного притяжения расширяется. При этом на границы области адгезионного притяжения влияет как форма штампа, закон его движения, так и упругие деформации поверхности полуплоскости, вызванные адгезией. По этой причине, границы области действия адгезионной силы заранее неизвестны и подлежат определению.
Был разработан численно-аналитический алгоритм, основанный на принципе суперпозиции [2]. Данный алгоритм позволяет определить носитель адгезионного притяжения в различные моменты времени в зависимости от параметров процесса. Была показана существенная зависимость скорости расширения границ носителя адгезионного притяжения от скорости движения штампа, его формы, а также от силы адгезионного взаимодействия. Представлены графические результаты для первого этапа взаимодействия штампа и упругой полуплоскости.
Работа выполнена при финансовой поддержке РФФИ (проект 16-08-00260 А).
1.Maugis D., Adhesion of spheres: The JKR-DMT transition using a Dugdale model // J. Colloid Interface Sci. 1992. 150 P. 243–269.
2.Горшков А.Г., Медведский А.Л., Рабинский Л.Н., Тарлаковский Д.В. Волны в сплошных средах. — М.: ФИЗМАТЛИТ, 2004.
Анатолий Сергеевич Оконечников
Финансовый университет при Правительстве РФ
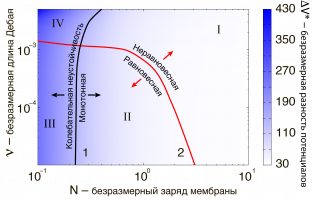
Известно, что при эксплуатации ионоселективных поверхностей возникает один из трех токовых режимов: допредельный (омический), предельный или сверхпредельный [1]. Большинство изученных сценариев возникновения сверхпредельных токов были рассмотрены из предположения идеальности ионоселективной мембраны [1, 2], а различные виды неидеальности мембраны рассматривались как небольшие количественные поправки к уже изученным явлениям. Однако, как показали последние исследования [3, 4], в неидеальных мембранах действуют качественно новые механизмы возникновения неустойчивости. Эти механизмы становятся еще более выраженными для концентрированных растворов электролитов, поведение которых гораздо менее изучено. Так, было показано, что наряду с электрокинетической неустойчивостью, которая вызвана электроосмотическим скольжением на границе зоны пространственного заряда, в системе с неидеальной мембраной также присутствует объемная неустойчивость.
На рисунке представлена карта режимов для двух ключевых параметров: число Дебая ν (отношение толщины двойного электрического слоя к толщине мембраны) и безразмерного заряда мембраны N(отношение заряда мембраны к равновесной концентрации ионов в электролите). На фоне цветом обозначено критическое значение безразмерной разности потенциалов (отношение разности потенциалов и термического потенциала). Кривая 1 разделяет области монотонной (I, II) и колебательной (III, IV) неустойчивостей, а кривая 2 – области равновесной (II, III) и неравновесной (I, IV) неустойчивостей. Для мембран с достаточно большим зарядом, которые близки к идеальным, всегда реализуется только классическая неравновесная электрокинетическая неустойчивость, в то время как с уменьшением заряда мембраны или увеличением концентрированности электролита проявляются новые равновесные и колебательные механизмы неустойчивости.
Работа выполнена при частичной финансовой поддержке РФФИ 18-08-01158-а и Министерства образования и науки Краснодарского края, проект № 16-48-230107-р_а.
Георгий Сергеевич Ганченко
ННГУ им. Н. И. Лобачевского
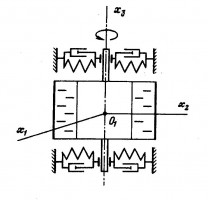
Исследование устойчивости стационарного вращения роторных систем с жидкостью представляет интерес как с общетеоретической, так и с прикладной точек зрения. Ранее был разработан оригинальный метод исследования устойчивости таких систем [1]. Предполагалось, что ось вращения ротора расположена в изотропных вязкоупругих закреплениях, а угловая скорость вращения поддерживается постоянной. В дальнейшем метод удалось обобщить и распространить на системы с анизотропными закреплениями оси ротора [2]. В работе [2] установлено влияние анизотропии жесткости закреплений оси ротора на форму границ областей устойчивости в пространстве параметров.
В данной работе исследуется устойчивость режима стационарного вращения типичной роторной системы с жидкостью, имеющей вязкоупругие закрепления оси ротора с анизотропией сил вязкости. Приведены примеры построения границ областей устойчивости в пространстве параметров и отмечено возникновение механических эффектов, вызванных анизотропией закреплений оси ротора.
1. Дерендяев H.В. Устойчивость вращения роторных систем, cодержащих жидкость: Монография. - Нижний Новгород: Изд-во Нижегородского госуниверситета, 2014.- 154 с.
2. Дерендяев Н. В., Дерендяев Д. Н. Исследование устойчивости стационарного вращения роторных систем с жидкостью. Труды Международной научной конференции «Фундаментальные и прикладные задачи механики». – Москва: изд-во МГТУ им. Н. Э. Баумана, 2017.- 222 с.
Дмитрий Николаевич Дерендяев
НИИ механики МГУ им. Ломоносова
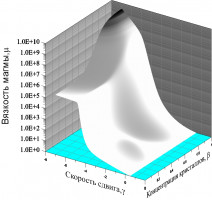
Традиционно течение магмы в канале вулкана описывается в рамках одномерных или квазиодномерных моделей с учетом зависимости вязкости от концентрации кристаллов и растворенной воды, температуры, возможности проскальзывания магмы вдоль стенок канала, неравновесной кристаллизации, оттока газа сквозь магму и в окружающие породы. В таких моделях профиль скорости считается параболическим и производится осреднение параметров поперек канала. Однако, за счет переменности свойств магмы поперек канала профиль скорости может существенно отличаться от параболического. В статье результаты расчетов по квазидвумерной модели сравниваются с одномерными. Показано существенное отличие как локальных характеристик, так и интегральной зависимости расхода магмы от давления в очаге.
Определяющие влияние на динамику вулканического извержения оказывает эволюция вязкости при подъеме магмы по каналу вулкана. При эксплозивном (взрывном) извержении нижняя часть канала занята пузырьковой жидкостью, верхняя – газовзвесью. Вязкость несущей фазы меняется скачкообразно при фрагментацими магмы [1]. При экструзивном извержении магма поднимается к поверхности без фрагментации, ее вязкость сильно увеличивается за счет выделения растворенного газа и кристаллизации. При больших концентрациях кристаллов магма проявляет неньютоновские свойства, ее вязкость зависит от скорости сдвига [2] так же наблюдается проскальзывание магмы по стенкам канала.
1. Ю.Б. Слезин, Динамика дисперсионного режима вулканических извержений: 1. Теоретическое описание движения магмы в канале вулкана. Вулканология и Сейсмология, 1983, № 5, с. 9-17.
2. Caricchi L. et al. Non-Newtonian rheology of crystal-bearing magmas and implications for magma ascent dynamics //Earth and Planetary Science Letters, 2007, Т. 264, №. 3-4, С. 402-419.
Юлия Дмитриевна Цветкова
Механико-математический факультет МГУ имени М.В. Ломоносова
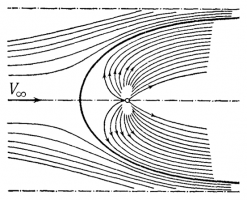
Известно, что при обтекании точечного источника (рис.1) с массовым расходом ρQ набегающим потоком со скоростью V, на источник будет действовать сила -ρQV. При движении сферической плавящейся частицы в собственном расплаве также необходимо учитывать изменение размеров частицы. Учет этих эффектов приводит к тому, что в уравнения движения частицы необходимо вводить реактивную силу, которая может существенно влиять на характер движения, как это было отмечено в [1] для случая идеальной жидкости. В работе [2] показано, что при наличии достаточно большого перепада температуры между частицей и расплавом данная сила может превышать силу вязкого сопротивления, что приводит к ускорению. частицы. Получен простой критерий, определяющий характер движения частицы в зависимости от относительного перепада температуры, числа Прандтля и относительной разности плотностей расплава и частицы.
На основании выведенных уравнений решается задача о случайном движении частицы, причём плавящейся за конечное время. Обнаружено, что среднеквадратичное отклонение такой частицы от начального положения за время плавления может быть даже неограниченно велико при больших перепадах температуры.
Уравнения движения частицы в вязком расплаве при отсутствии внешних сил допускают интеграл движения, учитывающий изменение кинетической энергии, который может быть использован при построении общей статистической теории плавящихся частиц. Решается уравнение Лиувилля для системы невзаимодействующих частиц и выводится выражение для давления как функции плотности сохраняющегося числа частиц и общей равновесной температуры расплава. В результате получена гиперболическая система уравнений движения континуума частиц на фоне механических и тепловых параметров расплава.
Для исследования особенностей движения континуума частиц решаются одномерные задачи с плоскими волнами: об однородном движении плавящихся частиц при нестационарном изменении температуры неподвижного расплава, а также о стационарном движении при постоянной температуре, проявляющая свойство запирания, связанное с невозможностью перехода через скорость звука, аналогичная газодинамической задаче о точечном источнике.
Работа частично поддержана грантом РФФИ № 17-01-00037.
1. А. Н. Голубятников. О взаимодействии плавящихся частиц о моделировании гравитации. // Вестник Нижегородского университета им. Н. И. Лобачевского, 2011. №4 (3). С. 728-729.
2. О. О. Иванов. К движению плавящейся частицы. // Вестник Московского университета. Сер. Математика. Механика, 2018 (в печати).
Олег Олегович Иванов
ФГУП "ЦАГИ"
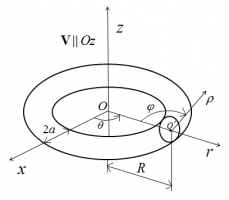
Изучение динамики вихревого кольца представляет большой интерес, так как вихревое кольцо позволяет исследовать механизмы образования шума в турбулентных течениях. Этот объект легко может быть создан в опыте для экспериментального исследования и допускает теоретическое описание как стационарных, так и колебательных режимов. В то же время, теоретическое изучение динамики вихревого кольца в виду ее сложности проводится лишь в приближении тонкого вихревого кольца [1]. Параметр тонкости вихревого кольца определяют, как отношение характерного радиуса сечения ядра вихревого кольца к радиусу вихревого кольца (рис. 1). Из всевозможных течений выделяется движение изохронного вихревого кольца, для которого период обращения жидких частиц внутри ядра вихревого кольца постоянен. Для такого вихревого кольца отсутствуют возмущения непрерывного спектра, что существенно облегчает проведение аналитических расчетов [2].
В этой задаче применяется подход, основанный на использовании поля смещения [3] как основной функции. Для исследования малых колебаний вихревого кольца этот подход использовался в работе [2], где впервые были правильно описаны бочкообразные моды вихревого кольца, а затем другие колебания.
В работе обсуждается возможная неустойчивость вихревого кольца, которая может реализовываться за счет взаимодействия колебаний разных типов, имеющих энергию разного знака (колебания с положительной энергией и колебания с отрицательной энергией [3]). Сложность задачи заключается в том, что вырождение собственных колебаний и количественное установление их связи может проявляться только при учете пятого приближения по параметру тонкости . В работе [2] вычисления проведены с точностью до . В данной работе получено дисперсионное уравнение в приближении и отработана процедура получения следующих приближений. Отметим, что для получения решения в следующих приближениях требуются более глубокие разложения не только колебаний, но и стационарного решения.
Работа выполнена по гранту РНФ, проект 17-11-01271.
1.Fraenkel L.E. Examples of steady vortex rings of small cross-section in an ideal fluid, J. Fluid Mech., 1972
2.Kopiev V.F., Chernyshev S.A. Vortex-ring eigen-oscillations as a source of sound, J. Fluid Mech.,1997.
3.Копьев В.Ф., Чернышев С.А. Колебания вихревого кольца, возникновение в нем турбулентности и генерации звука // УФН. 2000. Т. 170. № 7. С. 713-742.
Роман Валерьевич Акиньшин
Московский Государственный Университет имени М.В. Ломоносова
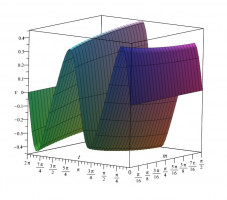
Рассматривается одномерное адиабатическое движение с плоскими волнами совершенного идеального газа в лагранжевых переменных. При этом уравнения движения сводятся с использованием массовой переменной к системе с квадратичной нелинейностью. Решение ищется, в частности, в виде рядов для закона движения газа и давления по степеням косинуса от временной переменной с коэффициентами, зависящими от массы. Для построения ряда требуется задать три первых коэффициента. Все остальные коэффициенты вычисляются рекуррентным образом по заданным при условии ненулевой производной первого коэффициента ряда для закона движения. Преимуществом данного подхода перед разложением решения, например в тригонометрический ряд Фурье, является именно конечность алгебраических рекуррентных соотношений, связанных только с вычислением производных по массе. Проводятся численные расчеты, которые показывают высокую сходимость ряда при определенных ограничениях на производные от задаваемых коэффициентов. Дальнейшим обобщением развитого подхода является представление решения в виде суммы одного ряда по степеням косинуса и произведения синуса на другой аналогичный ряд. При этом условием рекуррентной разрешимости является неравенство нулю разности квадратов производных первых членов, указанных выше рядов. Развивается соответствующий вычислительный процесс. Приводятся примеры, не содержащие особенностей.
Работа частично поддержана РФФИ (проект 17-01-00037)
Рис. Пример графика скорости потока на периоде
Дмитрий Владимирович Украинский
НИИ механики МГУ
Моделирование турбулентных течений жидкости и газа, вероятно, является одной из наиболее распространенных прикладных задач математической физики, для решения которых применяются суперкомпьютеры. Использование вихреразрешающих методов позволяет получить высокую точность результатов моделирования, однако требует больших расчетных сеток и длительных расчетов по времени для набора турбулентной статистики. Одним из способов повышения эффективности таких расчетов является использование алгоритма расчета турбулентных течений, предложенного в [1] и [2], который сочетает традиционный подход на основе осреднения по времени с усреднением по ансамблю реализаций этого течения. Это позволяет уменьшить длину интервала набора статистики для каждой из реализаций и заменить один длительный расчет на расчеты нескольких более коротких интервалов интегрирования по времени.
Особенностью данного алгоритма является необходимость генерации множества некоррелированных статистически стационарных турбулентных полей, используемых в качестве начальных данных при осреднении. Простейшим способом решения данной проблемы является моделирование процесса перестроения течения и выхода на турбулентный режим для различных начальных данных. Этот подход на практике обеспечивает некоррелированность полей скоростей, но требует значительных вычислительных затрат, сокращая преимущества метода. В настоящей работе предлагается оптимизированный способ генерации начальных турбулентных полей, основанный на внесении случайных возмущений в процессе выхода течения на турбулентный режим. Обсуждается область применимости данного подхода и возможное ускорение расчета. Полученные оценки подтверждаются результатами численных расчетов, которые демонстрируют существенное расширение области применимости метода и 10-20% повышение эффективности расчетов в целом.
Работа частично поддержана грантом РФФИ 17-01-00140-а. Для расчетов использовалось оборудование Центра коллективного пользования сверхвысокопроизводительными вычислительными ресурсами МГУ имени М.В. Ломоносова.
1. Makarashvili V., Merzari E., Obabko A., Siegel A., Fischer P. A performance analysis of ensemble averaging for high fidelity turbulence simulations at the strong scaling limit // Computer Physics Communications, vol. 219, p. 236-245, 2017. doi: 10.1016/j.cpc.2017.05.023
2. Krasnopolsky B. An Approach for Accelerating Incompressible Turbulent Flow Simulations Based on Simultaneous Modelling of Multiple Ensembles // Computer Physics Communications, 2018. doi:10.1016/j.cpc.2018.03.023
Борис Иосифович Краснопольский
Пермский государственный гуманитарно-педагогический университет
Известно, что периодические возмущения во вращающейся жидкости распространяются в виде инерционных волн [1]. Эти волны существуют благодаря действию силы Кориолиса и широко распространены как океанах, так и в жидких ядрах планет. В свою очередь колебания жидкости, обусловленные их распространением, могут приводить к возникновению интенсивных течений, изучению которых посвящена настоящая работа.
Экспериментальная установка представляет быстро вращающуюся вокруг горизонтальной оси кювету с цилиндрической полостью, заполненной маловязкой жидкостью. Для генерации волн скорость вращения меняется по гармоническому закону (либрации). Это приводит к возникновению осциллирующего движения в вязких пограничных слоях, в результате чего из мест соединения боковой и торцевых стенок цилиндра в объем жидкости распространяются инерционные волны. Обнаружено, что вблизи мест отражения волн от боковой стенки полости в пограничном слое Стокса возникает осредненное течение в виде осесимметричных тороидальных вихрей, скорость осредненного движения в которых пропорциональна квадрату амплитуды либраций. При определенных частотах либраций инерционные волны испытывают пространственный резонанс, формируя в объеме полости крупномасштабные осциллирующие структуры (так называемые инерционные моды). Последние являются собственными модами колебаний жидкости для данной геометрии полости. Резонансное возбуждение инерционных мод не только модифицирует осредненное течение, но и увеличивает его интенсивность в несколько раз.
Работа выполнена при поддержке гранта Президента Российской Федерации (проект МК-1994.2018.1).
1. Гринспен Х. Теория вращающихся жидкостей. Л.: Гидрометеоиздат. 1975. С. 304.
Станислав Валерьевич Субботин
МГУ им. М.В. Ломоносова
Неустойчивость течений жидкости и других физических систем может быть двух видов. В первом случае, когда ограниченные в пространстве растущие возмущения (волновые пакеты) сносятся потоком из любой заданной области, неустойчивость конвективная, а если растут вверх и вниз по потоку – то абсолютная [1]. Известно, что в струйных течениях и течениях в виде следа за телом с “классическими” профилями скорости неустойчивость всегда конвективная, а абсолютной она может становиться лишь при наличии достаточно сильного возвратного течения [2, 3] (в частности, возникновение дорожки Кармана при Re>47 объясняется как результат абсолютной неустойчивости стационарного обтекания цилиндра [4]).
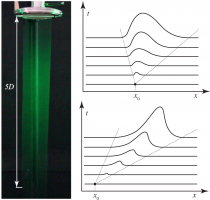
Однако, при анализе устойчивости затопленных струй, создаваемых устройством [5], было обнаружено, что неустойчивость, порождаемая точкой перегиба в профиле скорости, вблизи выходного отверстия устройства является абсолютной. Анализ механизма абсолютной неустойчивости показал, что для её возникновения необходимы два условия: (1) скорость в точке перегиба должна быть мала, (2) крутизна падения скорости в точке перегиба должна быть достаточно высокой. При выполнении обоих условий возникает 1:1 резонанс между вверх и вниз бегущей волной, что и даёт абсолютную неустойчивость. В то время как в классических профилях [2, 3] выполняется лишь второе условие, в струях с профилями скорости [5] – оба, что приводит к абсолютной неустойчивости без необходимости наличия возвратного течения жидкости.
При удалении от выходного отверстия профиль скорости в окрестности точки перегиба изменяется из-за действия вязкости (струя “расплывается”), и оба условия (1), (2) перестают быть выполненными на расстоянии лишь половины диаметра струи от выходного отверстия. В результате, в эксперименте абсолютная неустойчивость не наблюдается. Обсуждается меры к предотвращению “расплывания” струи для экспериментального наблюдения абсолютной неустойчивости.
Работа поддержана грантом РФФИ 18-38-00745-мол_а.
1.Уизем Дж. Линейные и нелинейные волны. М.: Мир, 1977. 638 с.
2. P. Huerre, P. A. Monkewitz. Absolute and convective instabilities in free shear layers// J. Fluid Mech. 1985. V. 159. P. 151-168.
3. M. Abid, M. Brachet, P. Huerre. Linear hydrodynamic instability of circular jets with thin shear layers// Eur. J. Mech., B/Fluids. 1993. V. 12. N 5. P. 683-693.
4. B. Pier. On the frequency selection of finite-amplitude vortex shedding in the cylinder wake// J. Fluid Mech. 2002. V. 458. P. 407-417.
5. J. Zayko, S. Teplovodskii, A. Chicherina, V. Vedeneev, A. Reshmin. Formation of free round jets with long laminar regions at large Reynolds numbers// Phys. Fluids. 2018. V. 30, 043603.
Василий Владимирович Веденеев
НИИ механики МГУ имени М.В. Ломоносова
Исследуется устойчивость уравнений Сен-Венана — уравнений, в гидравлическом приближении описывающих движение потоков в руслах и на склонах. Известно, что 1) малые мелкомасштабные возмущения в безграничном однородном потоке представляются в виде суммы двух волн, движущихся без изменения формы; 2) малые крупномасштабные возмущения распространяются в виде одной волны, движущейся без изменения формы; также известно 3) условие устойчивости по отношению к одномерным возмущениям [1].
В данной работе устойчивость решений уравнений для потоков в руслах и на склонах изучается по отношению к двумерным возмущениям. Возмущения представляются в виде суммы синусоидальных волн с меняющейся во времени амплитудой. Получено дисперсионное уравнение, связывающее частоту и волновой вектор возмущений; исследование знаков корней дисперсионного уравнения проводится с применением принципа аргумента (см. Рисунок). Получен критерий устойчивости: возмущения не растут тогда и только тогда, когда для действительных значений частот 1) мнимая часть дисперсионного уравнения имеет два корня, 2) вещественная часть дисперсионного уравнения положительна при подстановке меньшего из корней мнимой части и отрицательна при подстановке большего. Получена форма критерия, где в явном виде представлены ограничения на параметры исследуемого потока. Рассмотрены частные случаи для значений параметров, дающих характеристики потоков, близкие к реальным.
Юлия Сергеевна Зайко
Московский авиационный институт (национальный исследовательский университет)
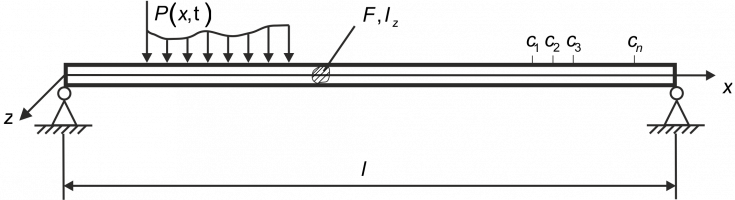
В прямоугольной декартовой системе координат рассматривается однородная изотропная балка конечной длины, исследование поперечных колебаний которой производится на основе уточненной теории, соответствующей модели С.П. Тимошенко. В качестве граничных условий используются условия шарнирного опирания. Начальные условия нулевые. В начальный момент времени к балке прикладывается распределенная нагрузка, зависящая от координаты и времени. Требуется идентифицировать нестационарную нагрузку, воздействующую на балку Тимошенко.
В основу методики решения прямой задачи положен принцип суперпозиции, при котором перемещения и контактные напряжения связаны посредством интегральных операторов по пространственной переменной и времени. При этом ядрами последних являются функции влияния для балки Тимошенко [1] (рисунок 1). Эти функции представляют собой фундаментальные решения систем дифференциальных уравнений движения исследуемой балки. Их построение представляет собой отдельную задачу. Функции влияния находятся с помощью преобразования Лапласа по времени и разложений в ряды Фурье по системе собственных функций.
Решение обратной задачи сводится к решению системы независимых интегральных уравнения Вольтера I-го рода, которая является некорректной по Ж. Адамару вследствие вырожденности ядер интегральных операторов. Для регуляризации обратной задачи применяется дифференцирование левых и правых частей уравнений, приводящие к системе интегральных уравнений с невырожденными ядрами [2].
Для решения системы разрешающих обратную задачу интегральных уравнений разработан и реализован на ЭВМ численно-аналитический алгоритм, основанный на методе средних прямоугольников.
Выполнена проверка полученных результатов. Приведены примеры расчетов.
Работа выполнена при финансовой поддержке РФФИ (проекты № 18-58-00008, 16-08-00260).
1. Горшков А.Г., Медведский А.Л., Рабинский Л.Н., Тарлаковский Д.В. Волны в сплошных средах. — М.: ФИЗМАТЛИТ, 2004. — 472 с.
2. Вахтерова Я.А., Серпичева Е. В., Федотенков Г.В. Обратная задача об идентификации нестационарной нагрузки для балки Тимошенко // Известия Тульского государственного университета. Технические науки. — 2017. — № 4. — С. 82–92.
Яна Андреевна Вахтерова
Московский авиационный институт (национальный исследовательский университет)
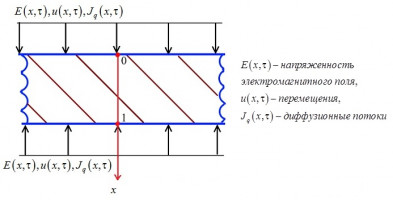
Математическая постановка задачи представляет собой связанную систему уравнений, состоящую из линейного уравнения движения сплошной среды, линейных уравнений массопереноса и уравнений Максвелла. Физические соотношения строятся с помощью метода термодинамических потенциалов для среды с произвольной анизотропией с использованием квадратичного приближения свободной энергии как функции деформаций, изменения концентрации веществ, входящих в состав среды и компонент векторов электрической и магнитной индукций. Предполагается, что упругая среда является идеальным твердым раствором. Кроме того, прямой пьезоэлектрический, пьезомагнитный и диффузионно-электрический эффекты слабо выражены. Это позволяет рассматривать задачу электродинамики отдельно. Её решение ищется в интегральной форме, представляющей собой свертку функций Грина с правыми частями граничных условий. Для построения функций Грина задачи электродинамики используется преобразование Лапласа и разложение в тригонометрические ряды Фурье. Найденные таким образом электромагнитные поля включаются в объемные возмущения задачи упругой диффузии, решение которой известно.
Николай Андреевич Зверев_old
Московский государственный университет им. М.В.Ломоносова
До недавнего времени был известен лишь один вид панельного флаттера — флаттер связанного типа, однако, в 2009-2010 годах было экспериментально доказано существование другого — одномодового типа панельного флаттера [1], который возникает при малых сверхзвуковых скоростях. Был проделан ряд работ по изучению одномодового флаттера, без учета пограничного слоя.
В первой части текущей работы изучается влияние возмущений пограничного слоя на устойчивость упругой пластины конечной длины в сверхзвуковом потоке газа при больших числах Рейнольдса. Исследование проводится в плоской постановке. Для решения задачи используется метод ВКБ-решений и асимптотический критерий глобальной устойчивости [2].
Получено, что в случае обобщенно выпуклого профиля пограничного слоя увеличение толщины слоя приводит к смещению частот растущих мод к более высоким значениям; при толстых пограничных слоях, пластина полностью стабилизируется. Для случая профиля с обобщенной точкой перегиба, увеличение толщины слоя сначала приводит к увеличению скорости роста возмущений. При больших толщинах, скорости возрастания возмущений уменьшаются при увеличении толщины пограничного слоя.
Эффект вязкости довольно сложен: есть собственные моды, которые стабилизируются вязкими возмущениями, и моды, которые дестабилизируются. Важным замеченным явлением, является то, что в диапазоне собственных частот, который соответствует самой высокой скорости роста в невязкой аппроксимации, влияние вязкости дестабилизирующее, т.е. скорость роста возмущений становится больше.
Во второй части работы численно исследуются сверхзвуковые течения газа с пограничным слоем над абсолютно жесткими поверхностями различных форм, с целью поиска и анализа устойчивых профилей пограничного слоя с обобщенной точкой перегиба, которые могут оказывать дестабилизирующее влияние на флаттер упругой поверхности.
Расчеты подтверждают возможность возникновения данных профилей слоя над криволинейными поверхностями. Обнаружены области (рассмотренных поверхностей), над которыми образуются искомые профили пограничного слоя, найдены границы этих областей — диапазоны длин от начальной кромки поверхности.
Работа поддержана грантами РФФИ №18-01-00404 и №18-31-00407.
1.Веденеев В.В., Гувернюк С.В., Зубков А.Ф., Колотников М.Е. Экспериментальное исследование одномодового панельного флаттера в сверхзвуковом потоке газа// Изв. РАН. МЖГ. 2010. № 2. С. 161-175.
2.Куликовский А.Г. Об устойчивости однородных состояний// Известия АН СССР. ПММ. 1966. Т. 30. Вып. 1. С. 148-153.
Всеволод Олегович Бондарев