Моделирование упругого ребра
Автор: Иван Викторович Алпатов
Организация: МГУ имени М.В.Ломоносова
Была поставлена глобальная задача моделирования грудной клетки для применения в лечении пациентов с килевидной деформацией. Подобное моделирование, особенно с помощью программ конечно-элементного анализа1, является своевременным и отвечающим запросам современной медицины.
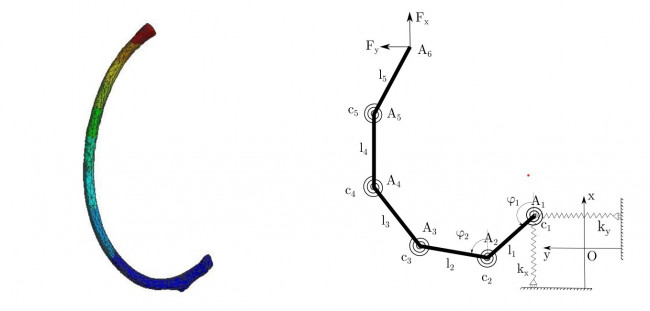
В данном исследовании была построена механическая модель плоского ребра под нагрузкой, приложенной к его концу. Модель ребра состоит из 5 абсолютно твердых стержней, соединенных между собой спиральными пружинами и расположенных в одной плоскости. Спиральная пружина в начале первого стержня препятствует повороту этого стержня в плоскости. Также начало первого стержня соединено цилиндрическими пружинами с двумя перпендикулярными друг другу неподвижными плоскостями, что моделирует податливость в синовиальном суставе головки ребра. В изначальном положении все пружины не деформированы.
Для данной системы были получены уравнения равновесия под действием плоской силы, приложенной к свободному концу ребра. При известных жесткостях пружин и геометрических параметрах ребра данная система позволит быстро вычислять деформированное состояние ребра. Геометрические параметры, а именно длины стержней и углы между ними в недеформированном состоянии были найдены с помощью специализированной медицинской программы 3D Slicer, позволяющей сегментировать необходимые области по КТ сканам пациентов. Для нахождения решения уравнений равновесия необходимо идентифицировать параметры – жесткости пружин.
Жесткости пружин находились из гипотезы равенства перемещений свободного конца ребра в стержневой модели и в модели ребра как криволинейной линейно-упругой однородной изотропной плоской балки. Перемещения в балочной модели находились численно с помощью интеграла Мора.
Также было произведено моделирование ребра в программе конечно-элементного анализа Ansys. Ребро моделировалось линейно-упругим изотропным материалом. Механические характеристики материала, такие как модуль Юнга, были взяты из литературы1. Для конечно-элементной модели было найдено напряженно-деформированное состояние. Различие перемещений свободного конца в рассмотренных моделях составляет не более 10%.


