Московский Государственный Университет имени М.В. Ломоносова
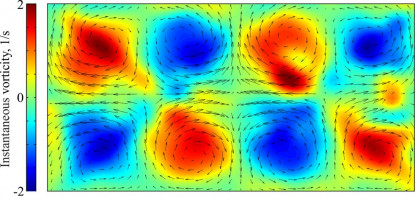
Рассматривается одномерное адиабатическое движение с плоскими волнами совершенного идеального газа в лагранжевых переменных. При этом уравнения движения сводятся с использованием массовой переменной к системе с квадратичной нелинейностью. Решение ищется, в частности, в виде рядов для закона движения газа и давления по степеням косинуса от временной переменной с коэффициентами, зависящими от массы. Для построения ряда требуется задать три первых коэффициента. Все остальные коэффициенты вычисляются рекуррентным образом по заданным при условии ненулевой производной первого коэффициента ряда для закона движения. Преимуществом данного подхода перед разложением решения, например в тригонометрический ряд Фурье, является именно конечность алгебраических рекуррентных соотношений, связанных только с вычислением производных по массе. Проводятся численные расчеты, которые показывают высокую сходимость ряда при определенных ограничениях на производные от задаваемых коэффициентов. Дальнейшим обобщением развитого подхода является представление решения в виде суммы одного ряда по степеням косинуса и произведения синуса на другой аналогичный ряд. При этом условием рекуррентной разрешимости является неравенство нулю разности квадратов производных первых членов, указанных выше рядов. Развивается соответствующий вычислительный процесс. Приводятся примеры, не содержащие особенностей.
Работа частично поддержана РФФИ (проект 17-01-00037)
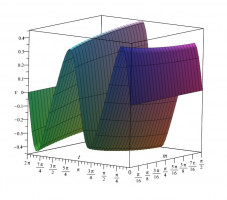
Рис. Пример графика скорости потока на периоде
Дмитрий Владимирович Украинский
Пермский государственный гуманитарно-педагогический университет
Известно, что периодические возмущения во вращающейся жидкости распространяются в виде инерционных волн [1]. Эти волны существуют благодаря действию силы Кориолиса и широко распространены как океанах, так и в жидких ядрах планет. В свою очередь колебания жидкости, обусловленные их распространением, могут приводить к возникновению интенсивных течений, изучению которых посвящена настоящая работа.
Экспериментальная установка представляет быстро вращающуюся вокруг горизонтальной оси кювету с цилиндрической полостью, заполненной маловязкой жидкостью. Для генерации волн скорость вращения меняется по гармоническому закону (либрации). Это приводит к возникновению осциллирующего движения в вязких пограничных слоях, в результате чего из мест соединения боковой и торцевых стенок цилиндра в объем жидкости распространяются инерционные волны. Обнаружено, что вблизи мест отражения волн от боковой стенки полости в пограничном слое Стокса возникает осредненное течение в виде осесимметричных тороидальных вихрей, скорость осредненного движения в которых пропорциональна квадрату амплитуды либраций. При определенных частотах либраций инерционные волны испытывают пространственный резонанс, формируя в объеме полости крупномасштабные осциллирующие структуры (так называемые инерционные моды). Последние являются собственными модами колебаний жидкости для данной геометрии полости. Резонансное возбуждение инерционных мод не только модифицирует осредненное течение, но и увеличивает его интенсивность в несколько раз.
Работа выполнена при поддержке гранта Президента Российской Федерации (проект МК-1994.2018.1).
1. Гринспен Х. Теория вращающихся жидкостей. Л.: Гидрометеоиздат. 1975. С. 304.
Станислав Валерьевич Субботин
МГУ им. М.В. Ломоносова
Неустойчивость течений жидкости и других физических систем может быть двух видов. В первом случае, когда ограниченные в пространстве растущие возмущения (волновые пакеты) сносятся потоком из любой заданной области, неустойчивость конвективная, а если растут вверх и вниз по потоку – то абсолютная [1]. Известно, что в струйных течениях и течениях в виде следа за телом с “классическими” профилями скорости неустойчивость всегда конвективная, а абсолютной она может становиться лишь при наличии достаточно сильного возвратного течения [2, 3] (в частности, возникновение дорожки Кармана при Re>47 объясняется как результат абсолютной неустойчивости стационарного обтекания цилиндра [4]).
Однако, при анализе устойчивости затопленных струй, создаваемых устройством [5], было обнаружено, что неустойчивость, порождаемая точкой перегиба в профиле скорости, вблизи выходного отверстия устройства является абсолютной. Анализ механизма абсолютной неустойчивости показал, что для её возникновения необходимы два условия: (1) скорость в точке перегиба должна быть мала, (2) крутизна падения скорости в точке перегиба должна быть достаточно высокой. При выполнении обоих условий возникает 1:1 резонанс между вверх и вниз бегущей волной, что и даёт абсолютную неустойчивость. В то время как в классических профилях [2, 3] выполняется лишь второе условие, в струях с профилями скорости [5] – оба, что приводит к абсолютной неустойчивости без необходимости наличия возвратного течения жидкости.
При удалении от выходного отверстия профиль скорости в окрестности точки перегиба изменяется из-за действия вязкости (струя “расплывается”), и оба условия (1), (2) перестают быть выполненными на расстоянии лишь половины диаметра струи от выходного отверстия. В результате, в эксперименте абсолютная неустойчивость не наблюдается. Обсуждается меры к предотвращению “расплывания” струи для экспериментального наблюдения абсолютной неустойчивости.
Работа поддержана грантом РФФИ 18-38-00745-мол_а.
1.Уизем Дж. Линейные и нелинейные волны. М.: Мир, 1977. 638 с.
2. P. Huerre, P. A. Monkewitz. Absolute and convective instabilities in free shear layers// J. Fluid Mech. 1985. V. 159. P. 151-168.
3. M. Abid, M. Brachet, P. Huerre. Linear hydrodynamic instability of circular jets with thin shear layers// Eur. J. Mech., B/Fluids. 1993. V. 12. N 5. P. 683-693.
4. B. Pier. On the frequency selection of finite-amplitude vortex shedding in the cylinder wake// J. Fluid Mech. 2002. V. 458. P. 407-417.
5. J. Zayko, S. Teplovodskii, A. Chicherina, V. Vedeneev, A. Reshmin. Formation of free round jets with long laminar regions at large Reynolds numbers// Phys. Fluids. 2018. V. 30, 043603.
Василий Владимирович Веденеев
НИИ механики МГУ имени М.В. Ломоносова
Исследуется устойчивость уравнений Сен-Венана — уравнений, в гидравлическом приближении описывающих движение потоков в руслах и на склонах. Известно, что 1) малые мелкомасштабные возмущения в безграничном однородном потоке представляются в виде суммы двух волн, движущихся без изменения формы; 2) малые крупномасштабные возмущения распространяются в виде одной волны, движущейся без изменения формы; также известно 3) условие устойчивости по отношению к одномерным возмущениям [1].
В данной работе устойчивость решений уравнений для потоков в руслах и на склонах изучается по отношению к двумерным возмущениям. Возмущения представляются в виде суммы синусоидальных волн с меняющейся во времени амплитудой. Получено дисперсионное уравнение, связывающее частоту и волновой вектор возмущений; исследование знаков корней дисперсионного уравнения проводится с применением принципа аргумента (см. Рисунок). Получен критерий устойчивости: возмущения не растут тогда и только тогда, когда для действительных значений частот 1) мнимая часть дисперсионного уравнения имеет два корня, 2) вещественная часть дисперсионного уравнения положительна при подстановке меньшего из корней мнимой части и отрицательна при подстановке большего. Получена форма критерия, где в явном виде представлены ограничения на параметры исследуемого потока. Рассмотрены частные случаи для значений параметров, дающих характеристики потоков, близкие к реальным.
Юлия Сергеевна Зайко
Московский государственный университет им. М.В.Ломоносова
До недавнего времени был известен лишь один вид панельного флаттера — флаттер связанного типа, однако, в 2009-2010 годах было экспериментально доказано существование другого — одномодового типа панельного флаттера [1], который возникает при малых сверхзвуковых скоростях. Был проделан ряд работ по изучению одномодового флаттера, без учета пограничного слоя.
В первой части текущей работы изучается влияние возмущений пограничного слоя на устойчивость упругой пластины конечной длины в сверхзвуковом потоке газа при больших числах Рейнольдса. Исследование проводится в плоской постановке. Для решения задачи используется метод ВКБ-решений и асимптотический критерий глобальной устойчивости [2].
Получено, что в случае обобщенно выпуклого профиля пограничного слоя увеличение толщины слоя приводит к смещению частот растущих мод к более высоким значениям; при толстых пограничных слоях, пластина полностью стабилизируется. Для случая профиля с обобщенной точкой перегиба, увеличение толщины слоя сначала приводит к увеличению скорости роста возмущений. При больших толщинах, скорости возрастания возмущений уменьшаются при увеличении толщины пограничного слоя.
Эффект вязкости довольно сложен: есть собственные моды, которые стабилизируются вязкими возмущениями, и моды, которые дестабилизируются. Важным замеченным явлением, является то, что в диапазоне собственных частот, который соответствует самой высокой скорости роста в невязкой аппроксимации, влияние вязкости дестабилизирующее, т.е. скорость роста возмущений становится больше.
Во второй части работы численно исследуются сверхзвуковые течения газа с пограничным слоем над абсолютно жесткими поверхностями различных форм, с целью поиска и анализа устойчивых профилей пограничного слоя с обобщенной точкой перегиба, которые могут оказывать дестабилизирующее влияние на флаттер упругой поверхности.
Расчеты подтверждают возможность возникновения данных профилей слоя над криволинейными поверхностями. Обнаружены области (рассмотренных поверхностей), над которыми образуются искомые профили пограничного слоя, найдены границы этих областей — диапазоны длин от начальной кромки поверхности.
Работа поддержана грантами РФФИ №18-01-00404 и №18-31-00407.
1.Веденеев В.В., Гувернюк С.В., Зубков А.Ф., Колотников М.Е. Экспериментальное исследование одномодового панельного флаттера в сверхзвуковом потоке газа// Изв. РАН. МЖГ. 2010. № 2. С. 161-175.
2.Куликовский А.Г. Об устойчивости однородных состояний// Известия АН СССР. ПММ. 1966. Т. 30. Вып. 1. С. 148-153.
Всеволод Олегович Бондарев
Пермский государственный национальный исследовательский университет
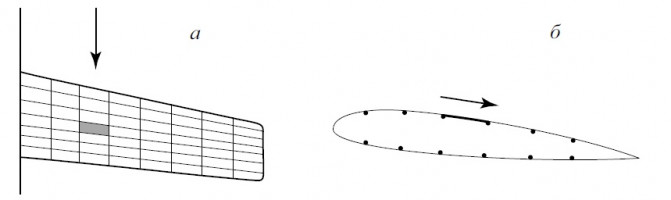
В последние годы в России были разработаны самолеты нового поколения и осуществлены их частные и государственные запуски. В связи с этим возникли новые сложные и крайне важные инженерные задачи. Так, на самолете МС 21 используются крылья из композитного материала, имеющего хорошие прочностные характеристики и низкую плотность, но, одновременно, большую чувствительность к высоким температурам. В связи с этим повреждение, например, системы кондиционирования способно привести к перегреву или даже к полному разрушению сегмента крыла. Подобные утечки случаются и в других технических ситуациях. К примеру, пробой газопровода может повлечь существенные экономические потери, а также привести к экологическому загрязнению. Таким образом, существует необходимость своевременного обнаружения и локализации разрывов трубопроводов.
Как правило, трубопровод окружен теплоизолирующей оболочкой, поэтому при повреждении нагретая жидкость не вытекает в окружающую среду, а просто прогревает (или охлаждает) теплоизоляцию изнутри. В результате на внешней поверхности трубопровода образуется температурная неоднородность, причем ее размер и форма будут зависеть не только от характера повреждения, но и его ориентации относительно вектора ускорения свободного падения. Поэтому в зависимости от локализации повреждения вокруг трубы возникнут разные конвективные структуры, исследование которых поможет спроектировать адекватные распределенные системы мониторинга.
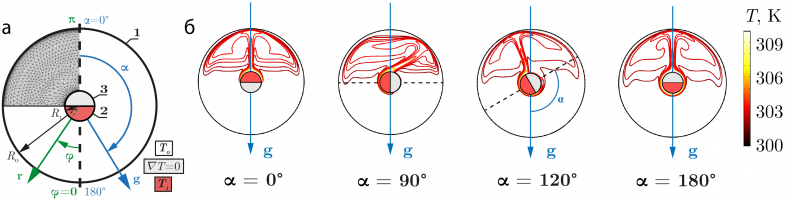
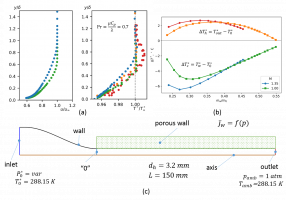
Так как при разрыве вытекающая жидкость часто остается под слоем тепловой изоляции, задача определения местоположения повреждения оказывается тесно сопряжена с процессом тепломассопереноса на внешней поверхности трубопровода. В качестве упрощения можно рассмотреть систему коаксиальных цилиндров с неравномерным подогревом [1, 2, 3]. Внешний цилиндр находится при температуре T0 и играет роль холодильника. Внутренний цилиндр разделён на две области в вертикальном направлении: одна половина теплоизолирована, другая поддерживается при постоянной температуре Ti > T0. Система находится в поле силы тяжести, причём вектор ускорения свободного падения g ортогонален оси цилиндров. Для имитации поворота внутреннего цилиндра, вектор g задаётся под некоторым углом α к вертикальной оси y.
Нами изучено влияние интенсивности нагрева и ориентации системы относительно направления вектора ускорения свободного падения g на структуру течения, распределение температуры в слое жидкости и интенсивность теплоотдачи. По результатам работы были сформированы требования к расположению и чувствительности элементов БРСКУ.
Матвей Максимович Гончаров
НИИ механики МГУ имени М.В. Ломоносова
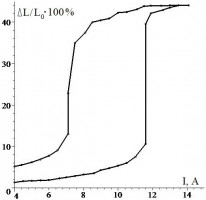
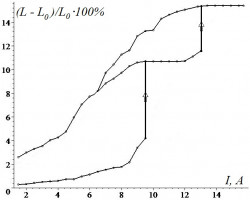
Намагничивающийся эластомер (НЭ) – это композитный материал, состоящий из упругой (вязкоупругой) основы и диспергированных в ней ферромагнитных частиц нано- или микроразмера. В докладе рассматривается проблема неоднозначности деформации этих материалов в магнитном поле. Исследуются, в частности, такие особенности поведения сферических и тонких тел из НЭ, как наличие двух устойчивых положений равновесия при фиксированной конфигурации магнитного поля (бистабильность), а также существование трех устойчивых положений равновесия тонкого тела из НЭ при определенном расположении двух электромагнитных катушек относительно его оси (мультистабильность). Данные эффекты были теоретически изучены в [1] и [2], соответственно. Также в докладе представлены эксперименты, в которых обнаружено существование двух и более чем двух равновесных форм тонкого тела из НЭ в неоднородном магнитном поле. На рисунке изображен экспериментальный график зависимости относительного удлинения тонкого тела от тока в электромагнитной катушке. Рассматриваются различные методики экспериментального определения параметров моделей упругого тела (модель Нео – Гука, Муни – Ривлина) и вязкоупругого тела (модель Кельвина – Фойгта с учетом пластических деформаций). Исследуются зависимости данных параметров от величины магнитного поля и влияние этой зависимости на характер деформации тел. Силовым методом определены магнитные свойства НЭ. Предложены способы создания анизотропных тел из НЭ. Построена модель анизотропного тела и экспериментально найдены параметры модели.
Исследования поддержаны РФФИ (18-501-12011, 18-31-00066, 16-31-60091).
1. Naletova V.A., Pelevina D.A., Merkulov D.I., Zeidis I., Zimmermann K., Bi-stability of the deformation of a body with a magnetizable elastomer in a magnetic field // Magnetohydrodynamics, Vol. 52, 2016, No. 3, pp. 287-298.
2. D.I. Merkulov, V.A. Naletova, D.A. Pelevina, V.A. Turkov, Multi-stability of a body with magnetizable elastomer in a non-uniform magnetic field // Journal of Magnetism and Magnetic Materials, Vol. 431, 2017, pp. 123-125, http://dx.doi.org/10.1016/j.jmmm.2016.10.011.
Дмитрий Игоревич Меркулов
НИИ механики МГУ имени М.В. Ломоносова
Проблема неоднозначности равновесной формы тела из намагничивающегося эластомера (НЭ) в неоднородном магнитном поле исследована во многих работах. Так, наличие двух устойчивых положений равновесия тел из НЭ при фиксированной конфигурации магнитного поля (бистабильность) обнаружено экспериментально в [1] и изучено теоретически в [2]. Однако при определенном расположении двух электромагнитных катушек относительно оси тела из НЭ возможно существование трех устойчивых положений равновесия (мультистабильность). Данный эффект впервые предсказан теоретически в [3].
В предлагаемой работе рассматривается эксперимент, посвященный обнаружению трех равновесных форм тонкого тела из НЭ в неоднородном осесимметричном магнитном поле двух электромагнитных катушек. Для его выполнения была сконструирована экспериментальная установка, состоящая из стеклянной трубки, на которой расположены две электромагнитные катушки, и внутри которой деформируется, не касаясь стенок, вертикальное тонкое тело из НЭ. Ток в катушках циклически увеличивался и уменьшался, и при этом измерялась координата нижнего свободного торца тела. По этим данным строился график зависимости относительного удлинения образца от тока в катушках. Обнаружено существование диапазона токов, при которых возможны три устойчивых положения равновесия тонкого тела из НЭ. Показан гистерезис длины тела при циклическом квазистатическом изменении тока в катушках. Предполагалось, что упругие свойства НЭ подчинялись модели Муни-Ривлина. Коэффициенты упругости в данной модели определялись экспериментально путем растяжения образца из НЭ в горизонтальном положении.
Таким образом, экспериментально показана возможность мультистабильности тонких тел из НЭ в осесимметричном магнитном поле системы двух электромагнитных катушек.
Исследования поддержаны РФФИ (18-501-12011, 18-31-00066, 16-31-60091).
1. Genoveva Filipcsei, Ildiko Csetneki, Andras Szilagyi, Miklos Zrinyi // Adv Polym Sci, Vol. 206, 2007, pp. 137-189. DOI 10.1007/12_2006_104
2. Naletova V.A., Pelevina D.A., Merkulov D.I., Zeidis I., Zimmermann K., Bi-stability of the deformation of a body with a magnetizable elastomer in a magnetic field // Magnetohydrodynamics, Vol. 52, 2016, No. 3, pp. 287-298.
3. D.I. Merkulov, V.A. Naletova, D.A. Pelevina, V.A. Turkov, Multi-stability of a body with magnetizable elastomer in a non-uniform magnetic field // Journal of Magnetism and Magnetic Materials, Vol. 431, 2017, pp. 123-125, http://dx.doi.org/10.1016/j.jmmm.2016.10.011.
Дмитрий Игоревич Меркулов
НИИ механики МГУ имени М.В. Ломоносова
В докладе представлены детали численного моделирования нового вида безмашинного энергоразделения, основанного на отсосе «холодных» слоёв пограничного слоя при высокоскоростном течении газа в канале с проницаемыми стенками. На базе уравнений Навье-Стокса, дополненных уравнениями неразрывности, энергии, а также k-e модели турбулентности построена математическая модель устройства, реализующего данный вид энергоразделения. Численное моделирование проводилось при использовании пакета ANSYS Fluent. Задача рассматривались в осесимметричной постановке. Разработано и протестировано специальное граничное условие вдува-отсоса на стенке.
При использовании экспериментальных данных [1, 2] проведена валидация математической модели. На основе разработанной модели проведены параметрические исследования. Проанализирован широкий диапазон режимов течения: от непроницаемой стенки до асимптотического отсоса. Показано влияние начального числа Маха, а также молекулярного числа Прандтля на величину энергоразделения.
Работа выполнена при поддержке Российского научного фонда проект № 14-19-00699.
Дмитрий Евгеньевич Хазов
Лаборатория вибрационной гидромеханики, Пермский государственный гуманитарно-педагогический университет

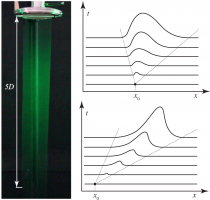
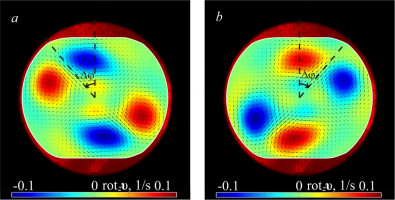
Работа посвящена экспериментальному изучению тепловой конвекции жидкости, заполняющей цилиндрический коаксиальный зазор с границами разной температуры при вращении вокруг горизонтальной оси. Рассматривается случай толстого слоя с более нагретой внутренней границей, когда центробежная сила инерции оказывает стабилизирующее воздействие на систему. Сила тяжести, вращающаяся в системе отсчета полости, является возмущающим фактором. На фоне колебаний неизотермической жидкости относительно полости, вызываемых осциллирующим внешним силовым полем, возбуждаются инерционные волны [1]. Обнаружено, что взаимодействие инерционных волн с неоднородным неизотермическим температурным полем приводит к генерации осредненных конвективных потоков. Волны, испытывающие многократное отражение от границ полости, формируют потоки неизотермической жидкости в виде системы азимутальных вихрей, не симметрично расположенных вдоль оси вращения (см. рис.).
Показано, что вибрационная конвекция, в основе которой лежат инерционные волны, распространяющиеся в неизотермической жидкости, проявляется даже в условиях устойчивой стратификации (при быстром вращении) до порога «классической» вибрационной конвекции [2]. Последняя возникает пороговым образом при понижении скорости вращения полости и проявляется в виде двумерных валов вытянутых вдоль оси вращения (см. рис.) на фоне азимутальных вихрей. Влияние допороговых конвективных течений усиливается с ростом разности температур на границах слоя.
Работа выполнена в рамках в рамках задания Минобрнауки (проект РФ 3.9053.2017/БЧ).
1. Kozlov V.G., Ivanova A.A., Vjatkin A.A., Sabirov R.R. Vibrational convection of heat-generating fluid in a rotating horizontal cylinder. The relative length of the cavity role // Acta Astronautica. 2015. Vol. 112. P. 48–55. DOI: 10.1016/j.actaastro.2015.03.014
2. Вяткин А.А., Козлов В.Г., Сираев Р.Р. О конвективной устойчивости жидкости во вращающемся горизонтальном цилиндрическом слое // Изв. РАН. МЖГ, 2017. № 4. С. 73–84.
Алексей Анатольевич Вяткин
Пермский государственный гуманитарно-педагогический университет
Двухжидкостные системы в виде эмульсий применяются во многих химических отраслях. В технологических процессах взвешенные капли жидкости подвергаются непрерывному изменению формы. Примером является ситуация, когда капля находится в осциллирующем сдвиговом потоке, что приводит к её периодическому сжатию и вытягиванию [1]. Если поверхность капли покрыта адсорбционной пленкой, межфазная граница оказывается тангенциально несжимаемой. Это означает, что в осциллирующем сдвиговом потоке такая капля одновременно с периодической деформацией будет совершать вращательные колебания. Исследованию структуры течения в модели такой капли посвящена настоящая работа.
Модель представляет собой кювету с эластичной упругой стенкой, совершающей вращательные колебания между двумя активаторами. В процессе колебаний в лабораторной системе отсчета форма полости остается неизменной. Обнаружено, что в области высоких безразмерных частот (толщина пограничных слоев мала по сравнению с размерами полости) и относительно малых амплитуд вибраций осциллирующее движение возбуждает осредненные крупномасштабные вторичные течения в виде двух пар согласованно вращающихся продольных вихрей. С увеличением амплитуды азимутальное течение, возникающее на долю полупериода колебаний полости, изменяет структуру среднего течения. Последнее принимает форму двух тороидальных вихрей, ориентированных вдоль оси вибраций. Изменение структуры течения сопровождается изменением зависимости осредненной скорости жидкости в вихрях от относительной амплитуды вибрационного воздействия. В области низких безразмерных частот осредненное течение состоит из двух пар продольных вихрей, совершающих вращательные колебания вместе с полостью. При этом направление движения противоположно тому, что наблюдается в высокочастотном пределе.
Работа выполнена при поддержке Российского Фонда Фундаментальных Исследований (проект 16-31-60099 мол_а_дк).
1. Cavallo R., Guido S., Simeone M. Drop deformation under small-amplitude oscillatory shear flow // Rheol. Acta 2003. Vol. 42. P. 1–9.
Станислав Валерьевич Субботин
Научно исследовательский институт механики МГУ им. М. В. Ломоносова
Аналитически и численно поставлены и решены плоские задачи о контуре и сопле максимальной тяги в сверхзвуковом потоке с ударными волнами.
Постулируется, что оптимизируемый контур, соединяющий две заданные точки А и C, причем ХA < XC и YA < YС, состоит из двух отрезков. Первый из них прямолинейный разворачивает однородный сверхзвуковой поток, имеющий место при X=XA и Y<YA, в волне разрежения Прандтля-Майера с центром в точке А на некоторый, заранее неизвестный угол Q, разгоняя его до значительных сверхзвуковых скоростей. Второй – в общем случае криволинейный, с неизвестной формой следует за первым с изломом в точке сопряжения В, XA < XB < XC, где образуется ударная волна, повышающая давление на этом отрезке контура.
Первая из рассмотренных задач носит модельный характер и относится к оптимальному профилированию хвостовой части тела с плоской нижней (или верхней) поверхностью, не возмущающей сверхзвуковой поток. В некоторой точке А указанная поверхность терпит излом, за которым контур тела должен прийти в некоторую точку С. В соответствии с высказанным постулатом ищется контур, соединяющий точки А и С, генерирующий ударную волну в своей точке излома и доставляющий максимум функционалу тяги. Взаимодействие сверхзвукового потока за волной Прандтля-Майера со стенкой на участке ВС моделируется по формуле Ньютона. Показано, что экстремаль состоит из двух отрезков прямых, причем второй составляет с первым угол Q/2. В зависимости от числа Маха М невозмущенного потока и удлинения профилируемой кормовой части тела λ = (XC - ХA)/(YС - YA) построены области существования экстремалей, соответствующие разным Q. Установлено, что каждому углу Q в плоскости параметров (М, λ) отвечает ограниченная кривая, концы которой при λ > 0.5 соответствуют коническому профилю – отрезку прямой, соединяющему точки А и С. Между указанными точками при изменении, например, одного из параметров – числа М достигается максимум отношения Т = ТO/ТС, где ТО – тяга оптимального, ТС – тяга конического контура, в некоторых случаях превышающий единицу на несколько десятков процентов. Точное решение соответствующей оптимизационной задачи в классе отрезков прямых значительно расширяет область существования "ударных" контуров и увеличивает их преимущество по сравнению с коническими контурами.
Вторая задача относится к построению плоского сверхзвукового сопла максимальной тяги с заданными координатами входа (ХA = 0, YA > 0 – критическое сечение сопла, в котором задано число Маха потока, несколько превышающее единицу: М=1.01) и выхода (XC, YС). Для приближенного определения формы экстремали на отрезке [XВ,XС] рассмотрена задача об оптимальной форме указанного отрезка при моделировании потока в сопле на отрезке [XА, XС] потоком от плоского сверхзвукового источника со звуковой линией, проходящей через точку А. Взаимодействие потока от источника со стенкой сопла на отрезке [XВ, XС] моделируется по формуле Ньютона. Показано, что каждый луч, выходящий из центра источника под некоторым углом φ ≤ Q, составляет в точке пересечения с элементарным отрезком экстремали угол φ/2. Следовательно, криволинейный отрезок экстремали является параболой, в фокусе которой располагается центр источника. С использованием построенного вычислительного кода, в котором использован метод Годунова, проведены параметрические расчеты течения в сверхзвуковой части сопла, состоящего из конического с углом Q и параболического участков, и его тяги, которая сравнивается с тягой эквивалентного конического сопла. Установлено, что в зависимости от определяющих параметров задачи тяга оптимального сопла, состоящего из прямолинейного отрезка и сопрягающегося с ним отрезка параболы, может превышать на несколько процентов тягу эквивалентного сопла с прямолинейной стенкой.
Работа выполнена при частичной финансовой поддержке РФФИ (проект № 18-01-00182).
Альберт Ришатович Мустаев
Центральный Аэрогидродинамический Институт имени Профессора Н.Е. Жуковского
Одним из основных источников шума самолета с реактивными двигателями является турбулентная струя. Интенсивность данного источника шума имеет сильную зависимость от скорости истечения струи. Данный факт помог достигнуть существенного прогресса по снижению шумности данного источника в современных двигателях повышенной степени двухконтурности, в которых скорость струи на фоне увеличенного диаметра сопла снижена. Тем не менее такой подход к данной проблеме носит свои ограничения, что приводит к необходимости поиска новых способов по управлению данным источником шума.
Из всех современных концепций снижения шума турбулентной струи при заданной скорости ее излучения в данной работе рассматривается система активного управления, основанная на непрерывном отслеживании в реальном времени состояния потока и реагировании на его возмущения с подстройкой управляющего воздействия таким образом, чтобы снизить нежелательные возмущения в потоке.
В качестве наиболее подходящего объекта активного управления в работе рассматриваются развивающиеся в слое смешения турбулентных струй крупномасштабные структуры, которые могут быть описаны теоретически с помощью представления о пакетах волн неустойчивости, растущих на начальном участке благодаря неустойчивости Кельвина-Гельмгольца и представляющих собой собственные решения исходных уравнений. Таким образом, подавление амплитуды волн неустойчивости должно напрямую вести к снижению шума высокоскоростных струй, для которых шум смешения все больше определяется данными структурами, но также и к снижению шума взаимодействия струи и крыла, так как в недавних исследованиях (например [1]) было показано, что для струи, установленной вблизи крыла, именно рассеяние пакетов волн неустойчивости на задней кромке крыла приводит к существенному усилению шума низко-, и высокоскоростных струй, поэтому управление волнами неустойчивости можно рассматривать также как универсальный подход к снижению шума конфигурации «струя-крыло».
В работе, являющейся продолжением работ [2, 3], представлены результаты экспериментальной диагностики волн неустойчивости в невозбужденных струях. Кроме того, разработан алгоритм управления волнами неустойчивости в невозбужденных струях, подходящий для использования в экспериментальных исследованиях. Принципиальная реализуемость предлагаемой концепции управления проверена на наборе данных, полученных при измерении ближнего поля невозбужденной струи.
Работа выполнена при финансовой поддержке РФФИ в рамках научного проекта № 18-31-00430.
1.Бычков О.П., Фараносов Г.А. О возможном механизме усиления шума струи вблизи крыла // Акуст. Журн. 2014. Т. 60. № 5. C. 596-610.
2.Беляев И.В., Зайцев М.Ю., Копьев В.А., Копьев В.Ф., Фараносов Г.А. Акустическое управление волнами неустойчивости в турбулентной струе // Акуст. Журн. 2013. Т. 59. № 1. С. 19-30.
3.Kopiev V.F. et al. // J. Phys. D: Appl. Phys. 2014. V. 47. P. 1-18.
Олег Павлович Бычков
НИИ механики МГУ, Москва
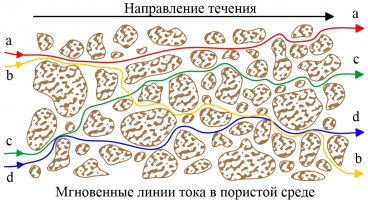
Многокомпонентные течения жидкостей и газов в пористых средах сопровождаются перемешиванием, приводящим к выравниванию полей концентрации – компонентного состава жидкости. К перешиванию приводит, во-первых, молекулярная диффузия, вызывающая перенос компонента жидкости в направлении противоположном градиенту его концентрации. Вторым механизмом перемешивания является механическая дисперсия в пористой среде, связанная с переменчивостью на масштабе отдельных пор поля скорости жидкости и соответствующим ветвлением траекторий движения элементарных частиц (Рис.) [1,2]. Интенсивность перемешивания из-за механической дисперсии зависит от направления и абсолютной величины средней скорости жидкости. В направлении, совпадающим с вектором средней скорости, интенсивность определяется различной скоростью движения частиц вдоль различных траекторий, а в перпендикулярном направлении – частотой ветвления траекторий. Во многих приложениях, как, например, при развитии слоистой конвекции в неизотермических фильтрационных течениях солёной воды, интенсивность перемешивания из-за механической дисперсии может на несколько порядков превышать интенсивность молекулярной диффузии.
В настоящей работе проведено расширение функциональных возможностей комплекса программ MUFITS [3] для численного моделирования неизотермических многокомпонентных многофазных течений в пористой среде. Разработан новый модуль для расчёта однофазной фильтрации с учётом механической дисперсий. Тестирование методов расчёта механической дисперсии, реализованных в модуле, проведено на одномерных и двухмерных задачах двухкомпонентной фильтрации соленой воды, допускающих аналитическое решение. Получены оценки для размеров шагов сетки по пространству и времени, при которых механическая дисперсия на порядок величины превосходит численную дисперсию. Обсуждаются особенности применения разработанного модуля к расчёту слоистой конвекции в пористой среде. Даны оценки скорости перемешивания из-за молекулярной диффузии и механической дисперсии при развитии конвекции.
Работа выполнена при финансовой поддержке РНФ (грант № 16-17-10199).
Рисунок: Схематическое изображение процесса механической дисперсии в пористой среде. В установившемся «осредненном» течении частицы жидкости, выпущенные в различные моменты времени из одно и той же точки (a/b; c/d), перемещаются вдоль различных траекторий.
1. Whitaker S. Diffusion and dispersion in porous media// AIChE J. 1967. V.13. P.420–427.
2.Sahimi M., et al. Dispersion in flow through porous media – I. One-phase flow// Chem. Eng. Sci. 1986. V.41(8). P.2103–2122.
3. Afanasyev A. MUFITS Reservoir Simulation Software. http://www.mufits.imec.msu.ru/
Андрей Александрович Афанасьев
НИИ механики МГУ имени М.В. Ломоносова
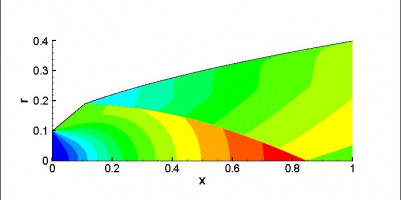
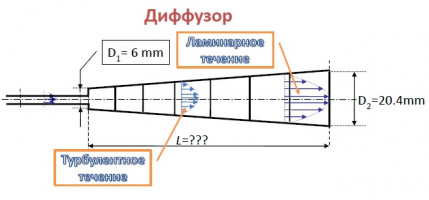
Проведены экспериментальные и расчетные исследования характеристик течения в коническом диффузоре с малыми углами раскрытия. На вход в диффузор подавалось развитое турбулентное течение. Расчет проводился с использованием трехпараметрической модели турбулентности [1]. Расчеты проводились, при числах Рейнольдса на входе в диффузор от 1000 до 10000 и c углами раскрытия меньше 4°. В зависимости от угла раскрытия в расчетах, течение в диффузоре происходило, при положительном, отрицательном или нулевом продольном градиенте давления. Получены характеристики течения на выходе диффузора, а также в различных сечениях вдоль диффузора. Результаты расчетов сравнивались с ранее полученными экспериментальными данными для диффузоров с углами раскрытия ~0.6° и ~1.2° [2], получено хорошее соответствие экспериментальных и расчетных данных.
Экспериментальные и расчетные данные показали, что в диффузоре, после начального участка, формируется турбулентное течение. Параметры турбулентного течения на выходе из диффузора определяются только числом Рейнольдса и не зависят от условий на входе, пока эти условия достаточны для формирования турбулентного течения.
Расчеты показали, что при увеличении длины диффузора турбулентное течение затухает и плавно переходит в ламинарное.
1. В.Г Лущик., А.А. Павельев, А.Е. Якубенко. Трехпараметрическая модель сдвиговой турбулентности //Известия РАН. Механика жидкости и газа. 1978. № 3. С. 13 - 25.
2. A.I. Reshmin, V.V. Trifonov, S.Kh. Teplovodskii. Turbulent flow in a conical diffuser with a small divergence angle at Reynolds numbers less than 2000 // ASME 2014, FEDSM2014-21597.
Владимир Викторович Трифонов