Научно-исследовательский институт механики МГУ им. М.В. Ломоносова, Москва
Проведены результаты экспериментальных исследований коэффициентов теплоотдачи и сопротивления на вихреобразующей поверхности в следе за поперечно установленным цилиндром. Коэффициент сопротивления определялся путем непосредственного взвешивания моделей на однокомпонентных тензометрических весах с учетом изменения статического давления на длине плавающих элементов. Для определения коэффициента теплоотдачи применялся метод нестационарного теплообмена с использованием ИК-камеры.
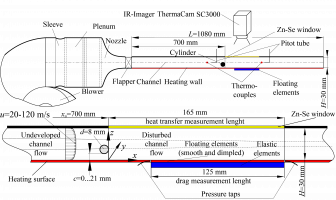
На расстоянии 796 мм от начала рабочего канала (длина 1080 мм, высота 30мм и ширина 300 мм) поперек потока (параллельно нижней стенке) устанавливался цилиндр диаметром d=8 мм. Зазор между нижней стенкой и цилиндром менялся в диапазоне 0-21 мм (цилиндр устанавливался с зазором в 0-11 мм с шагом 1 мм и с зазором 21 мм). Локальные значения коэффициентов теплоотдачи определялись на расстоянии x/d=0-20.625 от задней кромки цилиндра. Осредненные значения коэффициентов сопротивления определялись на участке x/d=12.5-20.625. В экспериментах исследовалась поверхность с шахматной компоновкой лунок с продольным и поперечным шагами 8 и 9 мм (глубина лунок – 1мм, диаметр пятна – 7.75 мм). Получены следующие результаты:
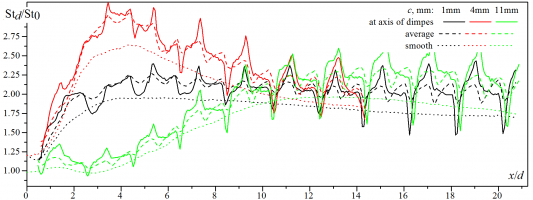
Значения относительного коэффициента сопротивления cxd/cxsm облуненной поверхности при зазоре c=21 мм незначительно превышает значение увеличения сопротивления в невозмущенном потоке. Далее величина cxd/cxsm растет при уменьшении зазора c. Это, по-видимому связано с тем, что величины коэффициентов сопротивления шахматных компоновок в невозмущенном потоке связаны с характерным взаимодействием лунок, расположенных в соседних рядах [1] – внесение крупномасштабных вихревых структур приводит к нарушению данного взаимодействия и увеличению коэффициента сопротивления.
Установка лунок приводит к увеличению неоднородности в поле коэффициентов теплоотдачи в следе за цилиндром в сравнении с гладкой стенкой. В первой части лунки (по направлению потока) наблюдается минимум коэффициентов теплоотдачи (по-видимому, вызванный наличием рециркуляционной зоны в этой области), у задней кромки наблюдаются максимальные значения коэффициентов теплоотдачи (область присоеднинения потока). При рассмотрении полей величин Std/St0 стоит отметить увеличение областей минимальных значений внутри лунок непосредственно за цилиндром (в области возвратных течений). Максимальные значения коэффициентов теплоотдачи при этом расположены при тех же значениях x/d, что и для гладкой стенке. Локальные значения интенсификации теплообмена на облуненной стенке варьировались в диапазоне Std/St0=0.9‑3.2 в зависимости от положения цилиндра.
Работа выполнена при поддержке грантов РФФИ № 18-08-00413 и СП-4006.2018.1.
1. van Nesselrooij M. et al. Drag reduction by means of dimpled surfaces in turbulent boundary layers // Exp. Fluids. Springer Berlin Heidelberg, 2016. Vol. 57, № 9. P. 1–14.
Николай Александрович Киселёв
Научно-исследовательский институт механики МГУ им. М.В. Ломоносова, Москва
Проведены результаты экспериментальных исследований коэффициентов теплоотдачи и сопротивления на гладкой и облуненной поверхностях в следе за поперечно установленным цилиндром. Коэффициент сопротивления определялся путем непосредственного взвешивания моделей на однокомпонентных тензометрических весах, для определения коэффициента теплоотдачи применялся метод нестационарного теплообмена.
На расстоянии 796 мм от начала рабочего канала (длина 1080 мм, высота 30мм и ширина 300 мм) поперек потока (параллельно нижней стенке) устанавливался цилиндр диаметром d=8 мм. Зазор между нижней стенкой и цилиндром менялся в диапазоне 0-21 мм (цилиндр устанавливался с зазором в 0-11 мм с шагом 1 мм и с зазором 21 мм). Локальные значения коэффициентов теплоотдачи определялись на расстоянии x/d=0-20.625 от задней кромки цилиндра. Осредненные значения коэффициентов сопротивления определялись на участке x/d=12.5-20.625 [1].
В экспериментах исследовались гладкая поверхность и поверхность с шахматной компоновкой лунок с продольным и поперечным шагами 8 и 9 мм (глубина лунок – 1мм, диаметр пятна – 7.75 мм).
Получены следующие результаты:
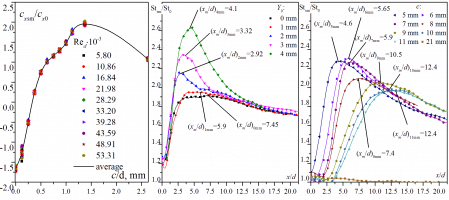
Значения коэффициента сопротивления гладкой поверхности cxsm/cx0, отнесенные к коэффициенту сопротивления гладкой поверхности в невозмущенном потоке cx0 менялись в диапазоне cxsm/cx0=(‑1.65)‑(1.95) в зависимости от положения цилиндра и не зависели от числа Рейнольдса набегающего потока. Локальные значения интенсификации теплообмена на гладкой стенке менялись в диапазоне Stsm/St0=1.0-2.65.
Значения относительного коэффициента сопротивления облуненной поверхности cxd/cxsm, менялись в диапазоне cxd/cxsm=(‑1.1)‑(1.3) (увеличивались при уменьшении зазора). Локальные значения интенсификации теплообмена на обуненной стенке варьировались в диапазоне Std/Stsm=0.8‑1.55 и практически не зависели от положения цилиндра.
Работа выполнена при поддержке грантов РФФИ № 18-08-00413 и СП-4006.2018.1.
1. Experimental investigation of the influence of large-scale vortex structures on heat transfer and drag on a smooth wall / N. A. Kiselev, A. G. Zditovets, Y. A. Vinogradov, M. M. Strongin // Journal of Physics: Conference Series. — 2017. — Vol. 891, no. 012149. — P. 1–8.
Николай Александрович Киселёв
Научно-исследовательский институт механики МГУ им. М.В. Ломоносова, Москва
Проведены результаты экспериментальных исследований коэффициентов теплоотдачи и сопротивления на гладкой поверхности в следе за поперечно установленным цилиндром. Коэффициент сопротивления определялся путем непосредственного взвешивания моделей на однокомпонентных тензометрических весах с учетом изменения статического давления на длине плавающих элементов. Для определения коэффициента теплоотдачи применялся метод нестационарного теплообмена с использованием ИК-камеры.
На расстоянии 796 мм от начала рабочего канала (длина 1080 мм, высота 30мм и ширина 300 мм) поперек потока (параллельно нижней стенке) устанавливался цилиндр диаметром d=8 мм. Зазор между нижней стенкой и цилиндром менялся в диапазоне 0-21 мм (цилиндр устанавливался с зазором в 0-11 мм с шагом 1 мм и с зазором 21 мм). Локальные значения коэффициентов теплоотдачи определялись на расстоянии x/d=0-20.625 от задней кромки цилиндра. Осредненные значения коэффициентов сопротивления определялись на участке x/d=12.5-20.625.
Получены следующие результаты:
Значения коэффициента сопротивления гладкой поверхности cxsm/cx0, отнесенные к коэффициенту сопротивления гладкой поверхности в невозмущенном потоке cx0 менялись в диапазоне cxsm/cx0=(‑1.65)‑(1.95) в зависимости от положения цилиндра и не зависели от числа Рейнольдса набегающего потока. Минимальные значения cxsm/cx0=-1.65±0.07 соответствуют c=0 мм (цилиндр расположен на стенке), максимальные значения cxsm/cx0= -1.96±0.06 соответствуют c=0 мм (цилиндр расположен на оси канала). При дальнейшем увеличении зазора c величина cxsm/cx0 начинает уменьшаться и достигает величины cxsm/cx0=1.08±0.03 при c=21 mm, т.е. при удалении цилиндра от стенки его влияние на динамический пограничный слой на стенке в канале практически не существенно.
Стоит отметить существенную неоднородность в распределении коэффициента теплоотдачи для всех положений цилиндра (кроме случая c=21 mm): сначала Stsm/St0 увеличивается от минимальных значений Stsm/St0=0.97-1.24 (наблюдаемых непосредственно у задней кромки цилиндра) до максимальных значений Stsm/St0=1.91-2.64 в зависимости от положения цилиндра. Положение максимума Stsm/St0 соответствует точке присоединения потока и, в диапазоне c=2-8 mm, находится в хорошем соответствии с зависимостью, предложенной в работе [1] для течения на пластине.
Работа выполнена при поддержке грантов РФФИ № 18-08-00413 и СП-4006.2018.1.
1. Suzuki K. et al. Study on a Turbulent boundary Layer Disturbed by a Cylinder-Effect of Cylinder Size and Position // Turbul. Shear Flows / ed. Durst F. et al. Berlin, Heidelberg: Springer Berlin Heidelberg, 1991. Vol. 7. P. 119–135.
Николай Александрович Киселёв
Институт гидродинамики им. М.А. Лаврентьева СО РАН
В повседневной жизни мы часто используем материалы, относящиеся к так называемой «мягкой материи» (soft matter). Так, например, шоколадный мусс, пена для бритья или строительная пена являются представителями широкого класса материалов с многомасштабной двухфазной структурой (газовые пузырьки в жидкой фазе) и имеют двойственное механическое поведение: твердые вещества в состоянии покоя, и жидкости, при воздействии напряжений, превышающих некоторый критический уровень. Такие специфические реологические свойства позволяют использовать пены в различных областях применения, от продуктов пищевой, косметической и фармацевтической промышленности до крупномасштабных промышленных процессов в области нефтедобычи и восстановлении почв. Таким образом понимание закономерностей, позволяющих осуществлять контроль течений пен в гетерогенных средах, представляется чрезвычайно важным [1 – 4].
Мы исследуем фундаментальные закономерности течения пен экспериментально в упрощенной модельной постановке. Эксперименты проводятся в ячейке Хеле-Шоу, представляющей собой простейшую модель трещины, образующейся, например, в процессе гидроразрыва пласта.
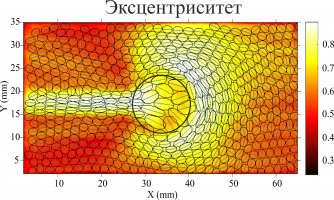
Исследовано течение пены в зависимости от нескольких параметров: величины и формы препятствия, помещенного в ячейку и локально сужающего ее зазор, и количества жидкости в пене. На Рис. 1 показано поле скорости (за вычетом скорости равномерного потока на входе в ячейку, направленного справа налево), демонстрирующее рециркуляцию, характеризующуюся наличием квадрупольного возмущения, а также ускорение пены вниз по течению от препятствия, что напоминает т.н. эффект «отрицательного следа» в течении за всплывающими воздушными пузырьками в вязкоупругих жидкостях [5].
Анализ экспериментальных данных показал, что интенсивность рециркуляционных течений зависит как от высоты препятствия, так и от свойств самой пены (сухая – жидкая): скорость потока вниз по течению от препятствия выше для сухой пены. Также было показано влияние горизонтального размера препятствия и его формы: в зазоре над квадратным препятствием возникают дополнительные особенности в виде вихрей на углах [6].
Работа выполнена при поддержке гранта МОН РФ № 14.W03.31.0002
1. Weaire D., Hutzler S. The Physics of Foams // Oxford University Press, 1999
2. Cantat I., Cohen-Addad S., Elias F., Graner F., Hohler R., Pitois O., Rouyer F. and Saint-Jalmes A. Foams, Structure and Dynamics // Oxford University Press, 2013
3. Dollet B., Graner F. Two-dimensional flow of foam around a circular obstacle: Local measurements of elasticity, plasticity and flow // J. Fluid Mech., 2007, V. 585 P. 181
4. Stevenson P. Foam Engineering: Fundamentals and Applications // Wiley, 2012
5. Hassager O. Negative wake behind bubbles in non-newtonian fluids // Nature, 1979, V. 279 P. 402
6. Chevalier, T., J. Koivisto, N. Shmakova, Alava M.J., Puisto A., Raufaste C., Santucci S. Foam flows through a local constriction //J. Phys. Conf. Ser., 2017, V. 925, P. 012025.
Наталья Дмитриевна Шмакова
НИИ механики МГУ
В технике хорошо известен эффект аэродинамического нагрева. Температура движущегося объекта в атмосфере близка к температуре торможения в результате перехода скоростного напора в теплоту. При сверхзвуковой скорости полета перед телом возникает головная ударная волна, за которая температура газа возрастает. При движении высокоскоростного потока в канале двигателя или в аэродинамической трубе обтекаемые поверхности разогреваются до температуры близкой к температуре торможения. Однако полного восстановления температуры до значения температуры торможения не происходит. Если стенка теплоизолирована, то температура пристенного слоя газа будет равняться температуре восстановления – в общем случае не равной температуре торможения. Мерой отклонения служит коэффициент восстановления температуры, показывающий долю энергии потока, переходящей в тепло на стенке.
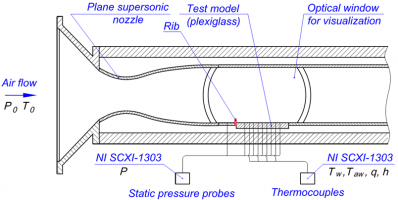
Интенсивность теплообмена при сверхзвуковых скоростях течения оценивают по коэффициенту теплоотдачи (числу Стентона), который с учетом эффектов сжимаемости определяется отношением теплового потока в стенку к разности между температурой стенки и температурой восстановления. При определении коэффициента теплоотдачи в данном случае основной проблемой является нахождение температуры восстановления, поскольку её непосредственное определение в эксперименте затруднено. Предложена методика одновременного определения коэффициентов теплоотдачи и восстановления температуры в процессе запуска сверхзвуковой аэродинамической установки до выхода на равновесный тепловой режим [1]. Регистрируя термогазодинамические параметры сверхзвукового потока с частотой 1 Гц, можно вычислить тепловой поток на стенке с помощью решения одномерного уравнения теплопроводности для полубесконечного тела.
Экспериментальные исследования проводились на сверхзвуковом аэродинамическом стенде (Рис. 1) с использованием систем регистрации данных National Instruments, автоматизированных программ опроса и обработки показаний сенсорных устройств в среде LabView, термопар с термокомпенсацией, зондовых измерений, тепловизионных и оптических методов визуализации картины течения.
Работа выполняется за счет гранта Российского научного фонда (проект №14-19-00699).
1. Виноградов Ю.А., Попович С.С., Стронгин М.М. Экспериментальное исследование коэффициента восстановления температуры и интенсификации теплоотдачи при течении на плоской стенке за ребром сверхзвукового потока сжимаемого газа. Наука и образование: научное издание МГТУ им. Н.Э. Баумана, 2016. № 11. С. 55-75, DOI: 10.7463/1116.0849557.
Сергей Станиславович Попович
Национальный исследовательский Томский государственный университет
В лабораторных условиях исследованы условия зажигания образцов древесины в результате теплового воздействия различного типа: 1) модельного низового лесного пожара 2) тлеющих частиц коры сосны. Установлено влияние огнезащитных покрытий (огне-био защитная пропитка для древесины «ФУКАМ», огнезащитная пропитка с антисептическим эффектом для древесины «Pirilax»-Classic», средства защитное для древесины «СЕНЕЖ ОГНЕБИО ПРОФ», а также огнезащитный состав «МИГ-09») на пожароопасные свойства древесины. Определены вероятность воспламенения и задержки зажигания древесины в зависимости от размера и количества горящих частиц, наличия воздушного потока в зоне падения частиц, а также в зависимости от начальной температуры древесины.
В качестве метода диагностики использовалась ИК-термография. В настоящее время ИК метод наряду с методами теплового неразрушающего контроля, не нарушающими целостности контролируемых объектов и не вносящими возмущения в процесс, представляет высокотехнологическую область прикладных исследований, которая объединяет достижения в теории теплопередачи, ИК технологии и компьютерной обработки экспериментальных данных.
В качестве исследуемых образцов строительных материалов были использованы: ДВП, ДСП, стеновая панель МДФ, древесный массив из хвойных пород. Методика проведения эксперимента, характеристики огнезащитных составов, используемых в эксперименте, а также предварительные результаты представлены в работах [1-3]. Имеющиеся данные, а также дополнительные эксперименты позволят установить зависимости показателей пожарной опасности строительных материалов от условий применения и типа огнезащитного состава, а также разработать лабораторный метод бесконтактной ИК-диагностики и контроля пожароопасных свойств древесных строительных материалов.
Работа выполнена при финансовой поддержке Гранта Президента РФ № МК – 3885.2018.8
Список литературы:
1.Д.П. Касымов, Е.Л. Лобода, А.С. Якимов, М.В. Агафонцев, Ю.А. Лобода Экспериментальное и численное моделирование воспламенения модели деревянного ограждения при тепловом воздействии фронта природного пожара // XXIХ Международная научно-практическая конференция, посвященная 80-летию ФГБУ ВНИИПО МЧС России: в 2 ч. М.: ВНИИПО, 2017. Ч. 2: Горение и проблемы тушения пожаров: тез. докл. (5 июля 2017 г.). с. 201–204.
2.D. Kasymov, M. Agafontsev Investigation of the Fire Hazard Characteristics of Wood Using Infrared Thermography // Proceedings of the 8th European Combustion Meeting. Dubrovnik, Croatia, 2017. p. 1484–1488. URL: http://www.adriacombustioninstitute.org/ecm2017/ (дата обращения: 29.09.2017).
3.D.P. Kasymov, A.A. Paletsky, M.V. Agafontsev Small-scale investigation of the fire hazard characteristics of wood samples due to the different type of thermal impact while forest fires / 9th INTERNATIONAL SEMINAR ON FLAME STRUCTURE Novosibirsk, Russia (July 10–14, 2017). Book of Abstracts. p. 51.
Денис Петрович Касымов
Финансовый университет при Правительстве РФ
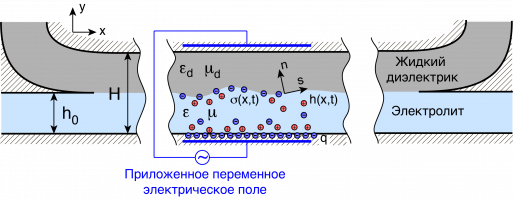
В данной работе рассматривается двухслойная система электролит-диэлектрик со свободной поверхностью раздела под действием внешнего электрического поля. Неустойчивость поверхности раздела является ключевым механизмом, ответственным за перемешивание. В микромасштабах отсутствует классическая гидродинамическая турбулентность, и для эффективного перемешивания в таких условиях необходимо искать другие эффекты, вызывающие неустойчивость одномерных течений и формирование микровихрей.
Для приведения жидкости в движение в микромасштабах обычно используют электрическое поле: оно действует на ионы солей, растворенных в жидкости, и приводит к электроосмотическому течению. Задача перемешивания жидкостей, в принципе, может быть решена аналогично: необходимо только подобрать условия, при которых электроосмотическое течение теряет устойчивость [1]. Существуют и другие способы создания неоднородности, в том числе за счет переменного электрического поля, направленного перпендикулярно каналу с жидкостями [2]. Переменное электрическое поле, особенно высокочастотное, является, к тому же, более предпочтительным по сравнению с постоянным, потому что при этом удается избежать нежелательных химических реакций, приводящих к деградации электродов и появлению пузырьков газа. Для случая, когда электрическое поле направлено вдоль границы раздела, было обнаружено два типа неустойчивости: длинноволновый и коротковолновый, связанные с поверхностными и объемными силами соответственно [3]. Если электрическое поле направлено по нормали к свободной поверхности раздела, то возникает неустойчивость, схожая с неустойчивостью Тонкса-Френкеля [4]. Для случая высокочастотных электрических полей получены асимптотические результаты.
Работа выполнена при финансовой поддержке Совета по грантам Президента Российской Федерации, грант для молодых кандидатов наук МК-5302.2018.1 и РФФИ грант 18-58-15004-НЦНИ_а.
Георгий Сергеевич Ганченко