Центральный аэрогидродинамический институт имени профессора Н.Е. Жуковского
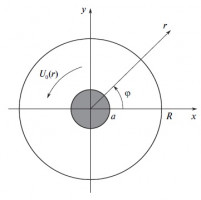
Данная работа является продолжением работ, посвященных неустойчивости цилиндра в циркуляционном потоке жидкости [1,2] и нацелена на более подробное изучение сдвиговой неустойчивости, возникающей в задаче. Сдвиговая неустойчивость представляет большой интерес, так как является причиной неустойчивости трехмерных вихрей, и по-видимому отвечает за турбулизацию вихревого кольца при больших числах Рейнольдса [3]. Исследование данной неустойчивости в трехмерных задачах представляет большие трудности. Задача о неустойчивости цилиндра радиуса a при обтекании его потоком жидкости с угловой скоростью U0(r), ограниченным стенками внешнего кожуха радиуса R (рис.1), представляется наиболее простой, в которой может быть выявлена сдвиговая неустойчивость, связанная с потоком энергии из критического слоя к колебаниям системы.
Ранее была решена задача о собственных колебаниях цилиндра в циркуляционном потоке жидкости [2]. Однако, собственные колебания не определяют полностью динамику этой системы, поскольку ее спектр содержит не только дискретную, но и непрерывную часть. В частности, представляет интерес начальная задача, решение которой является суперпозицией возмущений всего спектра.
Для исследования течения в области между цилиндрами используется аппарат поля смещения ε(r,t). Возмущение поля завихренности пропорционально радиальной компоненте поля смещения . Решение задачи Коши для поля смещения в кольце a<r<R выписывается в общем виде с помощью преобразования Лапласа. Для частных случаев (случай малой завихренности), интегралы могут быть вычислены точно. Таким образом, может быть построена зависимость завихренности от времени во всем течении.
Показано, что установление колебательного режима сопровождается перестройкой течения вблизи критического слоя. При этом поле смещения жидких частиц имеет сильно изрезанный характер и нарастающую по времени амплитуду.
Полученное решение для поля завихренности позволяет рассчитать поток энергии. Расчет потока энергии может быть проведен не только в случае малой монотонной завихренности, но и в точной постановке для течения с завихренностью обратно пропорциональной расстоянию до оси цилиндра.
Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант №16-01-00746).
Михаил Александрович Юдин
ФГУП «Центральный институт авиационного моторостроения имени П.И. Баранова»
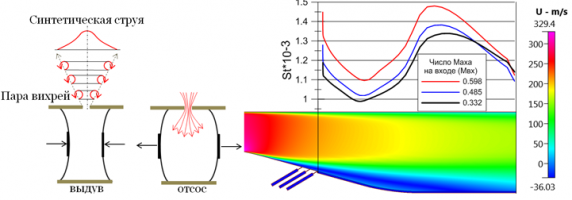
Синтетические струи с нулевым расходом газа являются перспективным активным средством управления течением в каналах ТРДД, с помощью которых можно добиться значительного сокращения потерь полного давления, за счет полной или частичной ликвидации отрывных зон. Для создания синтетических струй используется генератор синтетических струй (ГСС) (рис.1), который представляет собой независимую систему управления потоком, для его работы не требуется дополнительный расход воздуха, необходимо только подать энергию для возбуждения колебаний в пристеночной полости [1]. При работе ГСС увеличивается полный импульс пристеночного потока за счет роста скорости движения, отрыв потока при этом сокращается, и как следствие снижается тепловая нагрузка, так как в отрывных зонах тепловой поток в стенку значительно больше.
В данной работе расчет проводился в программном комплексе ESI-ACE+ с описанием газодинамических процессов в полости блоков ГСС с использованием URANS-методов в сочетании с SST-моделью турбулентности. При расчете использовалась модель реального воздуха с переменной теплоемкостью и температурой набегающего потока 1000К, которая соответствует приблизительной температуре потока на входе в переходный канал между турбиной высокого и низкого давления. Была выбрана система управления потоком из трех блоков ГСС с выдувом синтетических струй под углом 450 с частотой 1 кГц, расположенных последовательно в начале предполагаемой отрывной зоной на наклонном участке переходного канала [2]. В области отрыва с внешней стороны стальной стенки толщиной 3 мм задавалась температура 500К.
Расчетные исследования в модельном диффузорном канале с системой управления потоком показали, что при увеличении числа Маха на входе отрыв увеличивается и тем самым увеличивается тепловой поток в стенку в зоне обратного течения (рис. 2). При работе ГСС осредненное значение теплового потока в стенку за период меньше, чем без работы ГСС. Вследствие этого можно сделать вывод о том, что ГСС помогает не только сократить значение потерь в канале, но и уменьшить тепловую нагрузку на отдельные элементы конструкции.
Работа выполнена при поддержке гранта РФФИ 18-08-00271.
Список литературы:
1. Белова В.Г., Макаров А.Ю., Маслов В.П.,Степанов В.А. Проектирование блоков генераторов синтетических струй и экспериментальные исследования нестационарного истечения струй с помощью PIV-метода. Инженерный журнал: Наука и инновации, 2018, вып. 3.
2. Белова В.Г., Степанов В.А. Многопараметрические расчетные исследования генератора синтетических струй для активного управления течением в переходном канале. Инженерный журнал: Наука и инновации, 2018, вып. 4.
Валерия Геннадьевна Белова
НИИ механики МГУ
Снижение (редуцирование) давления газа на газораспределительных станциях (ГРС) от магистральных 50-120 бар до 6 бар в населенных пунктах приводит к существенному падению температуры газа (0.55 градуса на 1 бар). Процесс дросселирования приводит к образованию конденсата в виде газогидратов, обмерзанию регулирующих клапанов, запорной арматуры, приборов и трубопроводов. Для исключения эффекта гидратообразования на ГРС применяют системы подогрева газа. Блок подогрева представляет собой массивную конструкцию с котельной, на которой за счет сжигания части газа остальная часть подогревается.
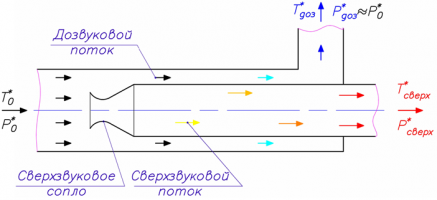
В технике известен способ безмашинного энергоразделения газового потока, который может быть использован для осуществления безогневного подогрева и редуцирования давления газа [1]. В основе данного метода лежит тепловое взаимодействие между сверхзвуковым и дозвуковым потоками, разделенными теплопроводной перегородкой (Рис. 1). Газ с начальным давлением P0* и температурой T0* разделяется на 2 потока: дозвуковой, текущий, например, по центральному каналу, и сверхзвуковой – по кольцевому, или наоборот. За счет теплообмена через разделяющую потоки стенку на выходе из устройства мы получаем потоки с разными температурами. Часть газа, поступающая в профилированное сверхзвуковое сопло, теряет полное давление при разгоне и торможении в диффузоре и подогревается за счет теплообмена через стенку с дозвуковым потоком. Газ, подаваемый во второй канал, сохраняет полное давление и охлаждается за счет теплоотдачи через стенку к сверхзвуковому потоку. Интенсивность нагрева или охлаждения зависит от соотношения расходов по сверхзвуковой и дозвуковой стороне.
Эффективность устройства сверхзвукового безмашинного энергоразделения определяется прежде всего количеством теплоты, передаваемой через разделяющую потоки стенку, который зависит от коэффициента теплопередачи, площади поверхности теплообмена, начальной температуры торможения потока и адиабатной температуры стенки, обтекаемой сверхзвуковым потоком.
Работа выполняется при поддержке гранта Фонда «НИР» компании «Иннопрактика» МГУ имени М.В. Ломоносова.
1.Vinogradov Y.A., Zditovets A.G., Leontiev A.I., Popovich S.S., Strongin M.M. Experimental research of shock wave processes influence on machineless gas flow energy separation effect // J. Phys. Conf. Ser. 2017. V. 891, N. 012080. DOI: 10.1088/1742-6596/891/1/012080.
Сергей Станиславович Попович
НИИ механики МГУ
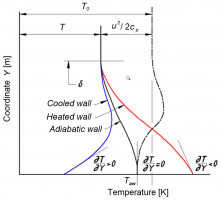
Вследствие вязкой диссипации в пограничном слое сверхзвукового потока сжимаемого газа происходит перераспределение температуры торможения. В результате температура торможения во внутренней части пограничного слоя – температура восстановления – оказывается ниже, а во внешней части – выше, чем температура торможения в основном потоке (для газов с числом Прандтля меньшем единицы). Определение температуры восстановления является одной из главных проблем при исследовании теплообмена сверхзвуковых потоков, поскольку ее непосредственное измерение в эксперименте затруднено. Для этого необходимо либо проведение длительных экспериментов на теплоизолированных моделях с достижением равновесного теплового режима, либо использование специальных методик математической обработки кратковременных экспериментов.
Внешние воздействия (градиент давления, проницаемость стенки, число Прандтля рабочего тела, форма и рельеф поверхности, скачки уплотнения и отрывные течения) могут приводить как к повышению аэродинамического нагрева в локализованной области, так и к охлаждению стенки. Известен эффект снижения адиабатной температуры стенки до значений ниже термодинамической температуры при поперечном обтекании дозвуковым сжимаемым потоком цилиндра в области задней критической точки (эффект Эккерта-Вайзе). Для сверхзвуковых потоков снижение температуры восстановления фиксируется в следе за обтекаемым препятствием в виде клина, ребра или ступеньки.
Эффект перераспределения температуры торможения в пограничном слое сжимаемого газа вследствие вязкой диссипации газа в пограничном слое играет важное значение в задачах расчета аэродинамического нагрева поверхности, объяснении эффекта аэродинамического охлаждения в следе за плохо обтекаемыми телами, эффекта газодинамической температурной стратификации и некоторых других. Сложность измерения температуры торможения с помощью термопары, помещенной в сверхзвуковой поток, заключается в том же самом эффекте восстановления температуры при обтекании спая термопары, как и любого другого предмета в сверхзвуковом потоке. В результате перераспределения температуры в пограничном слое термопара измеряет не температуру торможения, а температуру восстановления, что может вносить значительную погрешность в измерения.
Работа выполняется при поддержке стипендии Президента РФ СП-631.2018.1.
1.Leontiev A.I., Popovich S.S., Strongin M.M., Vinogradov Y.A. Adiabatic wall temperature and heat transfer coefficient influenced by separated supersonic flow // EPJ Web of Conf. 2017. V. 159. P. 1-5, DOI: 10.1051/epjconf/201715900030.
Сергей Станиславович Попович
НИИ механики МГУ имени М.В. Ломоносова, Москва/ ООО "Тесис", Москва
На сегодняшний день известно два основных вида сверхзвукового флаттера закрепленной с двух сторон пластины: связанный и одномодовый. Связанный флаттер достаточно подробно изучен и хорошо описывается поршневой теорией [1]. Математическое исследование одномодового флаттера появилось относительно недавно [2]. При этом, одномодовый флаттер представляет большую опасность для летательных аппаратов, поскольку возникает на низких сверхзвуковых скоростях и приводит к большим нагрузкам на их элементы конструкции.
Работа посвящена поиску путей снижения опасной нагрузки при флаттере упругой жестко закрепленной с двух сторон пластины. Исследования проводятся с использованием численного моделирования в программных комплексах Abaqus и FlowVision.
Одномодовый флаттер пластины, можно условно разделить на три основных вида: простой одномодовый флаттер с одной независимой частотой, резонансный флаттер с двумя кратными частотами и непериодический флаттер с двумя или более некратными частотами [3]. Наиболее опасными являются резонансный и непериодический флаттер. Возможны два варианта снижения ущерба от реализующегося флаттера: прохождение опасного участка на большом ускорении, не позволяющем развиваться наиболее опасным видам флаттера, или управление колебаниями за счет внесения возмущения.
В данной работе проведены исследования колебаний пластины в потоке, ускоряющемся и замедляющемся с разной интенсивностью, определены различия поведения пластины при разных значениях ускорения и замедления и определены значения ускорения и замедления потока, при которых не происходит развитие опасных видов флаттера. Также, проведено исследование влияния кратковременного возмущения на колебания пластины при постоянном и переменном внешнем потоке газа. Получено, что внесение возмущения приводит к изменению частоты колебаний и в ряде случаев, к развитию колебаний другого вида. Что, в свою очередь, позволяет предотвращать развитие наиболее опасных видов флаттера.
Исследования проводились в рамках проекта РФФИ 18-01-00404.
1. А.А.Мовчан. О колебания пластинки, движущейся в газе // Известия АН СССР. ПММ., 1956, Т. 20, Вып. 2., С. 211-222.
2. В. В. Веденеев. Предельные циклы колебаний при одномодовом флаттере пластины// ПММ. 2013. Т. 77. Вып. 3. С. 355-370.
3. Shishaeva A. S., Vedeneev V. V., Aksenov A. A., Sushko G. В.. Transonic panel flutter in accelerating or decelerating flow conditions// AIAA Journal, 2018, V. 56(3), P. 1-14.
Анастасия Сергеевна Шишаева
НИИ механики МГУ, Москва
Формирование порфировых месторождений цветных металлов связывают c образованием линз высококонцентрированных растворов соли [1]. При дегазации магматических очагов подобные линзы, содержащие в растворенном виде помимо соли также и цветные металлы, формируются на глубинах 1–2 км. Они находятся в условиях интенсивной конвекции воды, обусловленной высоким геотермическим градиентом, т.е. быстрым возрастанием температуры с глубиной. Если конвекция не размывает линзу, то создаются условия для формирования месторождения.
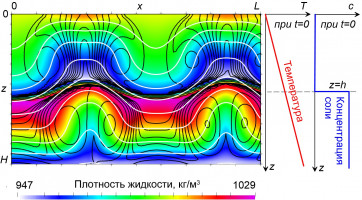
Для определения возможных условий существования линз рассмотрена нестационарная двухмерная задача фильтрации солёной жидкости в области (x,z)Î[0, L]´[0, H] (Рисунок), верхняя «открытая» граница которой z=0 соответствует поверхности Земли. На нижней границе z=H поддерживается повышенная температура (T), соответствующая заданному при t=0 линейному распределению T от z. При z<h концентрация соли (с) равна нулю, а при z³h она положительная константа. Предполагается, что плотность жидкости возрастает при уменьшении T или возрастании c. Таким образом, при t=0 имеется неустойчивая стратификации жидкости в областях z<h и z³h – плотность жидкости с глубиной z убывает, а при z=h плотность скачком возрастает.
В комплексе программ MUFITS [2] проведено прямое численное моделирование эволюции описанного распределения с учетом процессов теплопроводности, диффузии и механической дисперсии соли в пористой среде. Показано, что на начальном этапе развивается двухслойная конвекция с различными циркуляционными течениями в областях z<h и z³h [3], причем граница между жидкостями различной солености искривляется. Обнаружено два различных режима эволюции системы. При реализации первого режима конвективное течение полностью перемешивает жидкости различной солености, вынося соль через «открытую» границу z=0. Во втором режиме после начального переходного этапа, приводящего к незначительному перемешиванию жидкостей, система приходит к устойчивому положению равновесия, а конвекция прекращается. Причем, в области z³h сохраняются высокие значения концентрации. Первый и второй режимы определяют условия, при которых линза и месторождение не могут и, соответственно, могут образоваться.
Работа выполнена при финансовой поддержке РНФ (грант № 16-17-10199).
Рисунок: Распределение плотности жидкости; темными изолиниями показано распределение концентрации соли (с), а светлыми – температуры (T). Справа – начальные распределения T и c.
1. Afanasyev A., Blundy J., Melnik O., Sparks S. Formation of magmatic brine lenses via focused fluid-flow beneath volcanoes // Earth Planet. Sci. Lett. 2018. V.486. P.119–128.
2. Afanasyev A. MUFITS Reservoir Simulation Software. http://www.mufits.imec.msu.ru/
3. Griffiths R.W. Layered doubled convection in porous media // J. Fluid Mech. 1981. V.102. P.221–248.
Андрей Александрович Афанасьев
Механико–математический факультет, МГУ им. М.В. Ломоносова
Явление флаттера встречается в различных системах. Хорошо известен панельный флаттер - потеря устойчивости и интенсивные вибрации панелей обшивок летательных аппаратов, возбуждающихся при взаимодействии с потоком воздуха при больших скоростях полета. Обычно панельный флаттер приводит не к немедленному разрушению летательного аппарата, а к накоплению усталостных повреждений панелей. Одной из основных проблем, стоящих перед конструкторами современных газотурбиных двигателей, является флаттер лопаток. Как правило, для прогнозирования флаттера компрессорных лопаток используются упрощённые критерии, выработанные в конструкторских бюро на опыте проектирования и доводки двигателей.
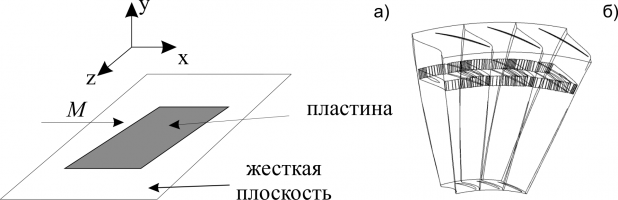
В докладе описывается применение энергетического метода [1] для решения двух задач: 1) Исследование одномодового флаттера пластин в форме прямоугольника, параллелограмма и трапеции (Рис. 1а); 2) Изучение влияния конструктивных параметров на прогнозирование флаттера лопаток компрессоров газотурбинных двигателей (Рис. 1б).
Суть энергетического метода заключается в следующем. Предполагается, что влияние потока воздуха на собственные колебания конструкции (лопатки или пластины) незначительно и сводится лишь к аэродинамическому демпфированию, положительному или отрицательному. При этом собственные формы и частоты колебаний конструкции в потоке и в пустоте совпадают и могут быть вычислены стандартными методами. Движение конструкции в потоке принудительно задается по собственной моде [2, 3], и решается нестационарная задача аэродинамики при заданных колебаниях конструкции. В результате решения вычисляется работа, совершенная силами давления на одном периоде колебаний. Критерием флаттера при таком подходе является положительность этой работы.
Были построены границы одномодового флаттера при разных значениях длины пластины. Получено, что границы одномодового флаттера трапециевидных пластин близки к границам одномодового флаттера прямоугольных пластин и при уменьшении значения угла скоса меняются незначительно. В противоположность этому, границы флаттера пластин в форме параллелограмма существенно отличаются от границ флаттера прямоугольных пластин и при уменьшении угла скоса увеличивается их аэроупругая устойчивость при малых сверхзвуковых скоростях. Также было исследовано влияние радиального и осевого зазора, угла прикрытия и открытия входного направляющего аппарата, радиальной неравномерности потока и величины монтажного натяга на результаты расчетов по прогнозированию флаттера лопаток. Показано, что влияние конструктивных параметров, кроме величины монтажного натяга, на границы флаттера незначительно. Значение же монтажного натяга существенно влияет на границы флаттера.
1. Vedeneev V.V., Kolotnikov M.E., Makarov P.V.. Experimental validation of numerical blade flutter prediction// Journal of propulsion and power. 2015. Vol. 31. No. 5. P. 1281-1291.
2. Абдухакимов Ф. А., Веденеев В. В. Исследование одномодового флаттера пластин различной формы при малой сверхзвуковой скорости// Ученые записки ЦАГИ. 2017. Т. 48. № 1. С. 86-98.
3. Абдухакимов Ф.А., Веденеев В.В., Колотников М.Е., Макаров П.В. Численное исследование влияния конструктивных параметров на прогнозирование флаттера лопаток// Проблемы машиностроения и надежности машин.(в печати).
Фаррух Адхамович Абдухакимов
ЦИАМ им. П.И. Баранова
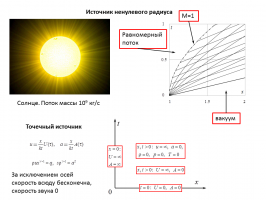
Получены решения начально-краевых задач об истечении идеального (невязкого и нетеплопроводного) совершенного газа из цилиндрических или сферических источников в пустоту. Время отсчитывается от момента включения источника, вне которого в момент включения – пустота. Фиксируются энтропийная функция, расход ("интенсивность" источника), равное или большее единицы начальное число Маха истекающего из источника газа, а также радиус начального цилиндра или сферы ("радиус источника"). Если радиус источника больше нуля, то область течения в плоскости "радиальная координата - время" состоит из двух подобластей: подобласти стационарного течения от источника и примыкающей к ней неавтомодельной центрированной волны разрежения (ЦВР) из С–-характеристик. Стационарное течение описывается известными конечными формулами, а ЦВР рассчитывается методом характеристик для одномерных нестационарных течений. При больших значениях радиальной координаты расчеты методом характеристик подтвердили полученные ранее асимптотические закономерности.
Граница между ЦВР и пустотой – прямая С0-характеристика (траектория частиц), совпадающая с граничной и единственной прямолинейной С–-характеристикой ЦВР. Она же – асимптота части С+-характеристик. Течение, возникающее при истечении в пустоту из источника с нулевым начальным радиусом, т.е. из "точечного" источника, принципиально отличается от описанного выше. В рассмотренной постановке при заданном конечном расходе и нулевом радиусе такого источника начальные скорость, плотность и скорость звука газа, истекающего из него, бесконечны. Вне зависимости от величины радиуса источника скорость газа и в стационарной части течения, и в нестационарной ЦВР с ростом радиальной координаты растет, а плотность и скорость звука уменьшаются. Показано, что такое же поведение этих параметров будет и для точечного источника. При этом скорость газа, будучи изначально бесконечной, остается такой всюду, а плотность и скорость звука, уменьшаясь, становятся нулевыми при любых ненулевых значениях радиальной координаты. При нулевом радиусе источника рассматриваемая задача становится автомодельной. Ее решение в плоскости "автомодельных" скорости и скорости звука дается тремя особыми точками дифференциального уравнения с этими переменными. Согласно сказанному выше в одной из них автомодельная скорость бесконечна, а автомодельная скорость звука равна нулю.
Работа выполнена при поддержке Российского фонда фундаментальных исследований (№ 17-01-00126).
Х.Ф. Валиев, А.Н. Крайко. Истечение идеального газа из цилиндрического или сферического источника в пустоту // Изв. РАН.Механика жидкости и газа. 2018. №5.
Харис Фаритович Валиев
ЦАГИ имени проф. Н.Е. Жуковского, Жуковский, Моск. обл.
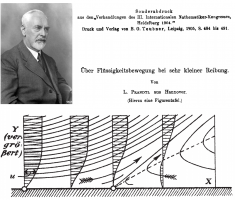
В докладе представлены исторические аспекты создания новых направлений в механике и в математике, связанные с новым подходом к исследованию проблем, содержащих малый параметр (или малые параметры). Эти подходы во многом связаны с именем Людвига Прандтля, создавшего как теорию пограничного слоя, так и методологию решения многих других задач с использованием асимптотических методов. Кроме истории создания этой теории представлены также и результаты, полученные в течение последующих 100 лет после публикации ключевой работы Прандтля. Обсуждаются перспективы дальнейших исследований, а также достигнутые результаты в области изучения устойчивости и перехода ламинарного пограничного слоя.
Рис. Сверху - Людвиг Прандтль и его труд «О движении жидкости с малым трением», 1904 г., снизу - пограничный слой на пластине (из работы Прандтля 1904 г.)
Игорь Иванович Липатов
Институт проблем механики им. А.Ю. Ишлинского РАН
Несмотря на то, что космическое пространство заполнено очень разреженным газом, для построения моделей физических явлений, встречающихся в космосе, часто используются методы гидроаэромеханики и магнитной гидродинамики. Это обусловлено, во-первых, тем, что обычно характерные масштабы этих явлений очень велики, а длины свободного пробега часто оказываются малыми по сравнению с ними. Во-вторых, космическое пространство заполнено в основном ионизованным газом, т.е. газом, который находится в состоянии плазмы. В последнем случае длины свободного пробега могут определяться не только парными кулоновскими столкновениями между заряженными частицами, но и так называемыми «коллективными» процессами, при которых длины свободного пробега существенно меньше длин свободного пробега в парных столкновениях, что дает возможность построения гидродинамических моделей. Активное развитие теоретических моделей тех явлений, которые встречаются в космическом пространстве, началось после того, как космические аппараты вышли в открытый космос, а приборы, устанавливаемые на них, смогли проводить прямые измерения гидродинамических параметров (скорости, плотности, температуры). Кроме того, появилась возможность исследования удаленных астрофизических явлений во всем диапазоне длин волн. Это, конечно, накладывает особую ответственность на ученых, занятых построением теоретических моделей, поскольку ценность модели определяется экспериментальным подтверждением ее выводов.
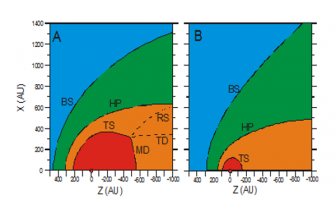
В настоящем докладе будут затронуты две проблемы, к которым автор имеет самое непосредственное отношение, а именно, взаимодействие солнечного ветра с межзвездной средой, окружающей солнечную систему, и с кометными атмосферами. Обе проблемы сводятся к газодинамическому или магнитогидродинамическому (МГД) взаимодействию двух сверхзвуковых потоков, в которых происходят химические реакции (процессы перезарядки, фотоионизации, ионизации электронным ударом и др.). Запуск космических аппаратов (КА) Voyager – 1, Voyager – 2, Pioneer – 10, Pioneer – 11 в середине 70-х годов прошлого столетия для изучения удаленных областей солнечной системы придал особую актуальность первой проблеме. Автору доклада вместе с сотрудниками и коллегами удалось построить пионерские модели с образованием двух ударных волн (в солнечном ветре и в межзвездной плазме) и тангенциального разрыва, разделяющего оба потока. В частности, в работе [1] впервые была предложена модель в ньютоновском приближении тонкого слоя. которая дала толчок к созданию реальной модели, учитывающей главный процесс резонансной перезарядки атомов Н, проникающими из межзвездной среды в солнечный ветер, с протонами [2]. Многие физические явления, предсказанные в модели [2], были через много лет подтверждены экспериментами на КА. В частности, на Рис. 1 приведены данные расчета формы и положения сильных разрывов, полученные в этой работе. Аппараты Voyager – 1 и Voyager – 2 пересекли ударную волну торможения солнечного ветра в 2004 и 2007 году на расстояниях 84 а.е. и 94 а.е., соответственно, что, с точностью ~ 3%, совпадает с предсказанным положением этой ударной волны (TS).
Для понимания процессов, которые происходят при взаимодействии солнечного ветра с кометными атмосферами, важным моментом были миссии космических аппаратов Вега – 1, Вега – 2, Giotto, Suissei и Sakigakе к комете Галлея в марте 1986 года и аппарата Rosetta к комете Чурюмова – Герасименко (2014 – 2016 годы). Пионерская работа по созданию гидродинамической модели в этой проблеме принадлежит авторам работы [3]. Применительно к исследованию кометы Галлея в марте 1986 года качественная модель в [3] была численно решена в работе [4], результаты которой хорошо совпали с данными экспериментов на космических аппаратах. В дальнейшем авторами работ [5 – 7] была развита МГД модель взаимодействия солнечного ветра с атмосферами комет Галлея, Григга – Шеллерупа и Чурюмова – Герасименко во время прохождения этих комет через перигелий.
Рисунок: Результаты численной модели взаимодействия солнечного ветра и межзвёздной звезды (Baranov and Malama, JGR, 1993). Левый рисунок не учитывает процесс резонансной перезарядки. Правый рисунок учитывает этот важный в проблеме эффект.
Автор выражает благодарность гранту РФФИ № 16-01-00305 за частичную финансовую поддержку доклада.
[1] Баранов В.Б., Краснобаев К.В., Куликовский А.Г., ДАН СССР, т. 194, стр. 41, 1970,
[2] Baranov V.B., Malama Yu.G., J. Geophys. Res., v. 98, pp. 15157 – 15163, 1993.
[3] L. Biermann, B. Brosowski, and H.U. Schmidt, Solar Phys., v. 1, p. 254, 1967
[4] Баранов В.Б., Лебедев М.Г., Письма в АЖ, т.. 12, стр.. 551, 1986
[5] Алексашов Д.Б., Баранов В.Б, Лебедев, Известия РАН, МЖГ, № 1, 2015
[6] Baranov V.B., Alexashov D.B., Lebedev M.G., MNRAS, v. 449, pp. 2268–2273, 2015
[7] Lebedev M.G., Baranov V.B., Alexashov D.B., Earth, Moon and Planets, v. 116, pp. 159 – 179, 2015
Баранов Владимир Борисович
ИТПМ СО РАН
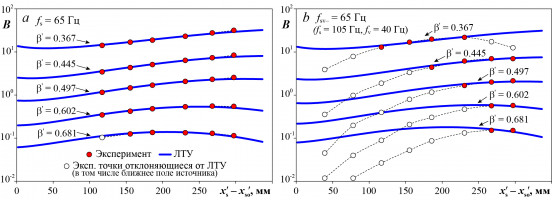
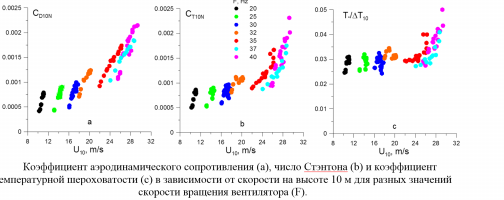
Настоящая работа направлена на изучение двух эффективных механизмов порождения в трехмерном пограничном слое на скользящем крыле мод неустойчивости поперечного течения (ПТ): локализованными вибрациями поверхности (1), а также за счет рассеяния на этих вибрациях вихрей набегающего потока (2). Исследование указанных задач восприимчивости проведено в рамках международного проекта RECEPT. Эксперименты проведены в пограничном слое экспериментальной модели с ламинаризированным крыловым профилем (угол скольжения 35°, хорда 0,8 м), которая была установлена в рабочей части малотурбулентной аэродинамической трубы MTL (КТИ, Стокгольм) под углом атаки –5 град. В результате, в экспериментальном пограничном слое нарастание мод неустойчивости Толлмина-Шлихтинга было подавлено благоприятным градиентом давления, а моды неустойчивости ПТ, напротив, могли усиливаться вниз по потоку. Эксперименты проведены с использованием метода контролируемых нестационарных возмущений. Источник локализованных вибраций поверхности представлял собой вибрирующую на частоте fs мембрану диаметром 6 мм. Мембрана была вмонтирована заподлицо с рабочей поверхностью экспериментальной модели на расстоянии ~130 мм от ее передней кромки. Двумерные вихревые возмущения потока генерировались вибрирующей на частоте fv проволочкой, которая была натянута параллельно передней кромке модели. Скорость набегающего потока составляла 10 м/c. Основные измерения выполнены однониточным датчиком термоанемометра.
Обнаружено, что оба исследуемых механизма восприимчивости приводят к достаточно эффективному порождению в пограничном слое пакетов трехмерных мод ПТ. В работе получены кривые нарастания амплитуд и фаз ПТ-мод, как порождаемых на частоте вибраций поверхности fs, так и на комбинационных частотах fsv± = fs ± fv. Получены оценки количественных характеристик исследуемых механизмов – амплитуды и фазы коэффициентов «вибрационной» и «вибрационно-вихревой» локализованной восприимчивости. Результаты получены в широком диапазоне параметров.
Верификация расчетов, выполненных по линейной (локально-параллельной) теории устойчивости (ЛТУ) показала, что эта теория способна надежно описывать развитие ПТ-мод на частоте fs (рис. 1а). Тем не менее, она не в состоянии объяснить эволюцию ПТ-мод, порождаемых на комбинационных частотах fsv± (рис. 1b). Анализ экспериментальных данных говорит в пользу того, что на частотах fsv± проявляется действие ранее не изученного механизма распределенной восприимчивости, связанного с рассеянием контролируемых вихрей набегающего потока на генерируемых вибрациями поверхности ПТ-модах. Изучение этого явления имеет большой научный и практический интерес.
Дмитрий Алексеевич Мищенко
Кубанский государственный университет
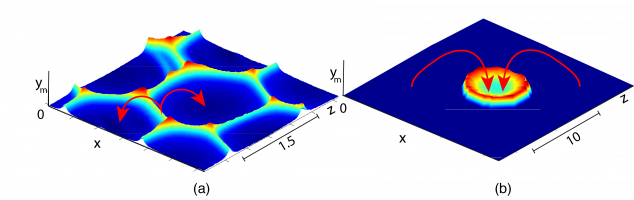
В последние десятилетия с развитием микро- и нанотехнологий ионоселективные поверхности нашли широкое применение в микроустройствах (например, лабораториях на чипе), что потребовало изучения их свойств в микро- и наномасштабах. Оказалось, что в электролите около таких поверхностей под действием внешнего электрического поля может скапливаться большой заряд, причем толщина заряженного слоя намного превосходит дебаевскую длину. Этот слой назвали зоной пространственного заряда. Пространственный заряд может быть неустойчивым, и при его возмущении развивается тангенциальное электрическое поле, которое приводит к электроконвективному движению [1]. Несмотря на множество практических приложений, наблюдается недостаток теоретических исследований в данной области. В частности, установки наподобие лабораторий на чипе часто не получают широкого распространения из-за невозможности добиться желаемых результатов в рамках изученных явлений. В свою очередь, большинство теоретических работ посвящено исследованию «чистой» электроконвекции, в то время как немногие, включающие в рассмотрение дополнительные эффекты (такие как Джоулев нагрев электролита [2]), показывают, что они могут приводить к качественно новым результатам.
Особенность данной работы заключается в том, что в модель включены дополнительные механизмы переноса электролита: помимо кулоновской силы, приводящей к электрокинетическим эффектам, в систему входит два механизма, связанных с подъемной силой. Первый из них – джоулев нагрев электролита, который приводит к возникновению термоэлектрокинетической неустойчивости [3], второй – это концентрационная конвекция, когда из-за неравномерного распределения соли меняется плотность электролита, и на его поведение начинает влиять сила тяжести [4]. Присутствие трех механизмов неустойчивости вызывает конкуренцию между ними. В работе получены критические значения параметров и составлена карта режимов.
Работа выполнена при частичной финансовой поддержке РФФИ 18-38-00611-мол_а
Наталья Юрьевна Ганченко
ИПФ РАН
Турбулентные потоки импульса и тепла на поверхности моря определяют обмен энергией и импульсом между атмосферой и океаном. На масштабе пограничного слоя, они являются ключевыми параметрами, которые определяют генерацию волн и формирование верхнего перемешанного слоя океана. Вопрос о коэффициентах обмена в приводном пограничном слое тесно связан с вопросом о влиянии поверхностного волнения, брызг, а также пены на обмен импульсом и массой между атмосферой и океаном.
Была выполнена серия экспериментов на Ветро-волновом канале ИПФ РАН по изучению процессов обмена импульсом и теплом в турбулентном пограничном слое воздушного потока над покрытой пеной взволнованной поверхностью. Эксперименты проведены в широком диапазоне скоростей ветра (диапазон изменения U10 в ходе эксперимента составил от 12 до 38 м/с) и параметров волнения. Для возможности непрерывного создания пены на поверхности воды был разработан специальный подводный пеногенератор, который не вносил бы существенного влияния на поверхностное волнение. Расход пены во всей серии экспериментов не изменялся.
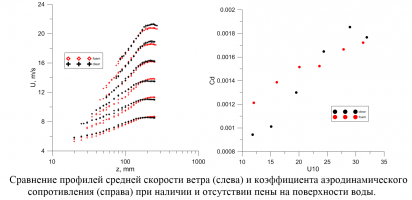
Используя разработанный ранее метод профилирования [1] средней скорости и температуры в рабочей секции канала были определены значения коэффициентов обмена импульсом и теплом. Построены зависимости коэффициентов обмена от параметров воздушного потока и характеристик волнения.
Работа выполнена при поддержке проектов РФФИ 18-05-00265, 18-55-50005, 17-05-00703, 16-55-52022, РНФ 14-17-00667, гранта Президента СП-1740.2016.1.
1. Yu. I. Troitskaya, D.A. Sergeev, A.A. Kandaurov, G.A Baidakov, M.A. Vdovin, V.I. Kazakov Laboratory and theoretical modeling of air-sea momentum transfer under severe wind conditions // JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 117, C00J21, 13 PP., 2012 doi:10.1029/2011JC007778
Максим Игоревич Вдовин
ИПФ РАН
Турбулентные потоки импульса, явного и скрытого тепла на поверхности моря определяют обмен энергией и импульсом между атмосферой и океаном. На масштабе пограничного слоя, они являются ключевыми параметрами, которые определяют генерацию волн и формирование верхнего перемешанного слоя океана. Вопрос о коэффициентах обмена в приводном пограничном слое (или о параметрах шероховатости) тесно связан с вопросом о влиянии поверхностного волнения, а также брызг на обмен импульсом и массой между атмосферой и океаном.
Была выполнена серия экспериментов на Ветро-волновом канале ИПФ РАН по изучению процессов обмена импульсом и теплом в устойчиво температурностратифицированном турбулентном пограничном слое воздушного потока над взволнованной поверхностью. Эксперименты проведены в широком диапазоне скоростей ветра и параметров волнения, включая экстремальные с интенсивным обрушением волн и образованием брызг. Для создания температурной стратификации пограничного слоя поступающий в канал воздух нагревался до 30-40 градусов. Температура поверхности воды при этом постоянной (около 15 градусов). Скорость ветра на оси канала от 8,8 м/с до 19 м/с, что соответствует эквивалентной скорости 10-35 м/с. Используя разработанный ранее метод профилирования [1] средней скорости и температуры в рабочей секции канала были определены значения коэффициентов обмена импульсом и теплом. Построены зависимости коэффициентов от параметров воздушного потока и характеристик волнения.
Было продемонстрировано, что в отличие от турбулентного потока импульса (скорости трения) и коэффициента обмена импульсом, температурная шероховатость (поток тепла) и, соответственно, коэффициент обмена теплом слабо зависит как от скорости, так и от параметров волнения до начала обрушения волн и генерации брызг. Брызги, которые начинают генерироваться тоже примерно после 27 м/с, приводят к сильному росту теплообмена, и тенденции к насыщению, как у коэффициента обмена импульсом, не наблюдается.
Работа выполнена при поддержке проектов РФФИ 18-05-00265, 17-05-00703, 16-55-52022и РНФ 14-17-00667, гранта Президента СП-1740.2016.1.
1. Yu. I. Troitskaya, D.A. Sergeev, A.A. Kandaurov, G.A Baidakov, M.A. Vdovin, V.I. Kazakov Laboratory and theoretical modeling of air-sea momentum transfer under severe wind conditions // JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 117, C00J21, 13 PP., 2012 doi:10.1029/2011JC007778
Максим Игоревич Вдовин
ИАП РАН
При полете в атмосфере метеорное тело со временем разрушается под действием увеличивающего скоростного напора, а также нагрева. В случае, если представленное тело является достаточно массивным, то оно может расколоться на отдельные фрагменты – осколки. Данные осколки затем продолжают свое движение в атмосфере совместно как группа тел.
Моделирование сверхзвукового полета группы осколков метеорного тела является актуальной проблемой вычислительной механики. При этом необходимо рассматривать большое количество вариантов возможных состояний систем в зависимости от количества образующихся осколков, их относительного положения, также размеров, формы и плотности отдельных фрагментов. В связи с этим целесообразным представляется решать сопряженную аэродинамическую и баллистическую задачи, и авторами был разработан метод численного расчета динамики системы тел [1]. Представленный метод дополнен алгоритмом для моделирования соударений между телами.
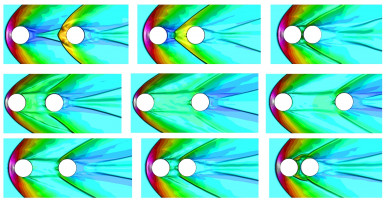
Рассмотрена задача о сверхзвуковом полете двух осколков метеорного тела изначально расположенных на одной линии вдоль вектора скорости. Так как лидирующее тело имеет большее сопротивление, то отстающее тело будет его догонять, постепенно втягиваясь в след лидирующего тела – эффект коллимации [2]. В результате тела столкнуться, обменяются импульсом и разлетятся. Со временем из-за меньшего аэродинамического сопротивления отстающее тело не только компенсирует разность скоростей тел, но и наберет скорость достаточную для того, чтобы опять догнать лидирующее тело, тела опять столкнуться, и процесс повторится (рис. - изменение картины течения со временем при числе Маха M=6).
Характер изменения амплитуды колебаний со временем позволяет предположить, что существует некоторое расстояние которое является равновесным для системы в заданных условиях.
1. Лукашенко В.Т., Максимов Ф.А. Математическая модель разлета осколков метеорного тела после разрушения // Инженерный журнал: наука и инновации. 2017. Вып. 9
2. Барри Н.Г. Ф.А. Аэродинамика фрагментов метеорного тела. Эффект коллимации // Астрономический вестник. 2010 . Т 44. № 1. С. 59–64.
Владислав Тарасович Лукашенко