Национальный исследовательский Томский государственный университет
Конвективный теплообмен во вращающихся полостях имеет многочисленные инженерные приложения, включающие в себя пищевые и химические процессы, охлаждение электронного оборудования, проектирование роторных систем и многое другое [1]. Целью настоящей исследования является численное моделирование конвективно-радиационного теплопереноса в квадратной вращающейся полости при наличии источника энергии постоянного объемного тепловыделения.
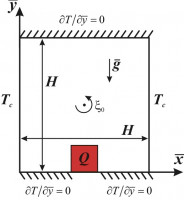
Полость, заполненная теплопроводной ньютоновской жидкостью, прозрачной для излучения, вращается против часовой стрелки с постоянной угловой скоростью 0. Вертикальные стенки поддерживаются при постоянной температуре Tc, горизонтальные стенки считаются адиабатическими. Внутри полости находится тепловыделяющий источник. Стенки полости являются диффузно-серыми. Теплообмен излучением между стенками анализируется в приближении поверхностного излучения.
Определяющие уравнения Обербека–Буссинеска записываются в безразмерном виде в переменных «функция тока–завихренность–температура» с учетом вращения системы [2]. Для упрощения анализа радиационного теплообмена используется метод сальдо, где безразмерная плотность радиационного потока определяется с помощью плотности потока эффективного излучения на основе условия теплового баланса. Для решения сформулированной краевой задачи используется метод конечных разностей. Дискретное уравнение Пуассона для функции тока решается отдельно методом последовательной верхней релаксации, уравнения дисперсии завихренности и энергии решаются с применением локально-одномерной схемы Самарского.
Численные исследования нестационарных режимов естественной конвекции и поверхностного теплового излучения в замкнутой вращающейся полости проведены в широком диапазоне изменения определяющих параметров. Исследовано влияние чисел Рэлея, Тейлора и Остроградского, а также приведенной степени черноты ограждающих стенок на распределения изолиний функции тока и температуры, а так же на среднюю температуру внутри источника энергии.
Работа выполнена при финансовой поддержке Российского научного фонда (проект № 17-79-20141).
-
You R., Li H., Tao Z. Experimental investigation on two-dimensional heat transfer and secondary flow in a rotating smooth channel // Int. J. Heat Mass Transfer. 2017. 113. P. 342–353.
-
Mikhailenko S.A., Sheremet M.A. Convective heat transfer combined with surface radiation in a rotating square cavity with a local heater // Numerical Heat Transfer A. 2017. 72. 697–707.
Степан Андреевич Михайленко
ФИАН им. П.Н. Лебедева
Рассматриваются свойства симметричной части тензора градиентов скорости, называемого тензором скоростей деформации, в развитом турбулентном потоке несжимаемой жидкости. На основании анализа численных данных [1, 2] обнаружена симметрия распределения тензора в однородном изотропном турбулентном потоке. Аналогичная симметрия получена аналитически для случая гауссового распределения скоростей [3].
Используя аналитическое выражение симметрии удается показать, что функция распределения нормированного собственного значения тензора [4, 5] имеет универсальный характер в обоих случаях.
Показано, что искажение симметрии распределения для малоинтенсивных пульсаций может быть связано с влиянием гауссовой крупномасштабной силы (или иного стохастического источника, поддерживающего стационарность потока), поскольку имеет ярко выраженный гауссов характер.
Исследование выполнено во ФГУП «Центральный аэрогидродинамический институт имени профессора Н.Е. Жуковского» за счет гранта Российского научного фонда (проект №17-11-01271)
1. Perlman E., Burns R., Li Y., Meneveau C. Data Exploration of Turbulence Simulations using a Database Cluster // Supercomputing SC07, ACM, IEEE., 2007.
2. Li Y., Perlman E., Wan M., Yang Y., Burns R., Meneveau C., Burns R., Chen S., Szalay A., Eyink. G. A public turbulence database cluster and applications to study Lagrangian evolution of velocity increments in turbulence // Journal of Turbulence, 2008, т. 9, № 31.
3. Kopyev A. V. Degeneracy of velocity strain-rate tensor statistics in random isotropic incompressible flows // Phys. Rev. Fluids, 2018, т. 3, 024603.
4. Kerr R. M. Histograms of helicity and strain in numerical turbulence // Phys. Rev. Lett., 1987, т. 59, № 7, 783-786.
5. Lund T. S., Rogers M. M., An improved measure of strain state probability in turbulent flows // Phys. Fluids, 1994, т. 6, № 5, 1839-1847.
Алексей Викторович Копьев
Центральный институт авиационного моторостроения имени П.И. Баранова
Выполнено сравнение термических коэффициентов полезного действия и удельных тяг и импульсов прямоточных реактивных двигателей разных типов с медленным ("дефлаграционным") горением (МГ) и с горением в движущихся (пульсирующих и вращающихся – «спиновых») и неподвижных детонационных волнах (ДВ). Актуальность такого сравнения обусловлена распространенными, особенно в последнее время, утверждениями о возможном увеличении тяговых характеристик воздушно-реактивных двигателей (ВРД) с горением в ДВ (в первую очередь, в пульсирующих – PDE и вращающихся – RDE) на десятки процентов в сравнении с прямоточными ВРД (ПВРД) с МГ при постоянном давлении в дозвуковом потоке. Подобные прогнозы, однако, опираются не на прямой расчет тяг этих двигателей, а на сравнение их идеальных термических коэффициентов полезного действия (кпд) – hth и на применимые только к стационарным течениям в инерциальных системах координат формулы, связывающие также идеальные удельные тяги и импульсы с идеальными кпд. Для PDE эти формулы неверны из-за нестационарности течения.
В России утверждения о преимуществах детонационного горения (ДГ) нередко сопровождаются ссылками на заметку Я.Б. Зельдовича [1] 1940 г., переведенную на Западе только в начале XXI века. Для незнакомых с этой заметкой ссылки на столь авторитетного ученого производят требуемый эффект в противоположность тому, что писал сам автор. Хотя Я.Б. Зельдович обнаружил некоторое увеличение термического коэффициента полезного действия (КПД) при ДГ, это не вызвало у него эйфории. Напротив, в той же заметке высказаны только скептические соображения о применении ДГ, например: "... поиски циклов с ДГ в погоне за небольшим увеличением принципиально достижимого кпд бесперспективны". Ни в этой, ни в других публикациях Я.Б. Зельдовича высказываний в поддержку ДГ нет.
В развитие [1, 2] выполнен термодинамический анализ разных типов ВРД с ДГ и МГ. В исследуемых далее ВРД горению почти всегда предшествует сжатие в воздухозаборнике поступающего из атмосферы со скоростью V0 воздуха и всегда заканчивается "расчетным" расширением в сопле продуктов сгорания до давления набегающего потока р0. В рассматриваемых моделях двигателей предварительное сжатие воздуха в воздухозаборнике и расширение продуктов сгорания в сопле принимаются изэнтропическими и стационарными. По определенным, как в [2], идеальным термическим кпд (hth) находится отношение Ve/V0, где Ve – скорость на выходе из сопла при расчетном расширении до р0. Удельные тяга и импульс пропорциональны разности (Ve/V0 – 1). Рассмотренные типы ВРД включают двигатели с МГ при постоянном давлении, как в ПВРД (по циклу Брайтона), и постоянном объеме (по циклу Хэмфри), пульсирующие детонационные двигатели (PDE) с горением в ДВ Чепмена - Жуге (ДВCJ), ВРД с горением в стационарных ДВCJ, в том числе, с предварительным торможением сверхзвукового потока (SDEy³1, y = Т3/Т0, Т0 и Т3 – температуры холодного воздуха и горючей смеси перед ДВ) и в косой ДВ – SDEOSW (при y = 1).
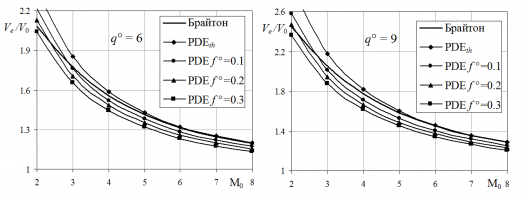
При фиксированных показателях адиабаты воздуха, горючей смеси и продуктов сгорания идеальные характеристики рассмотренных ВРД, предполагающие, как в [2], отсутствие потерь при торможении воздуха в воздухозаборнике, его смешении с газообразным топливом и истечении продуктов сгорания из реактивного сопла, зависят от двух безразмерных параметров: числа Маха полета М0 и q° = q/(cpT0) – безразмерной теплотворной способности горючей смеси (ср – теплоемкость при постоянном давлении). При q° = 6 и 9 сравнение идеальных кпд hth и рассчитанных по hth с помощью упомянутых выше формул (незаконных для PDE) идеальных удельных тяг и импульсов всех рассмотренных двигателей выполнено для М0 от 0.3 до 8. Для этих q° и М0 по такой идеальной тяге PDE незначительно превосходит ВРД с горением при постоянном объеме (по циклу Хэмфри), а ПВРД с МГ – намного только при М0 < 1.5. С ростом М0 превышение идеальной тяги PDE над идеальными тягами других ВРД за исключением SDEOSW быстро уменьшается. Так, при q° = 6 и 9 превосходство по идеальной тяге PDE над остальными становится малым при увеличении числа Маха полета М0.
Пусть PDE имеет n цилиндрических, синхронно работающих групп детонационных камер (ДК) с мгновенно открывающимися и закрывающимися клапанами (входными силовыми стенками). При открытых клапанах в ДК поступает идеально перемешанная горючая смесь. Период работы одной ДК PDE можно разбить на несколько этапов: 1. Открытие клапана, заполнение ДК горючей смесью, мгновенные закрытие клапана и инициирование ДВ волны у входного конца ДК; 2. Приход ДВ на правый конец ДК – сечение входа в идеально регулируемое реактивное сопло; 3. ДВ отражается от правого частично открытого сечения ДК (сужения сопла) как ударная волна (УВ), которая движется к закрытому входному сечению ДК. Далее нестационарные ударные волны, двигаясь по ДК, могут несколько раз отразиться от ее концов. Несмотря на затухание, отражающиеся УВ – не учитываемый при определении идеальных характеристик PDE источник роста энтропии. Клапан мгновенно открывается, когда среднее давление продуктов сгорания в ДК становится меньше давления заторможенного воздуха и идеально перемешанного с ним топлива в объеме перед клапаном.
Истечение продуктов сгорания происходит на протяжении всего цикла работы PDE. Течение в расширяющейся части сопла квазистационарное и изэнтропическое, площадь выходного сечения сопла идеально регулируемая. Расчёты проводились в рамках одномерной задачи в приближении уравнений Эйлера. Система уравнений одномерной нестационарной газовой динамики численно решалась с помощью явной монотонной распадной разностной схемы второго порядка (для гладких решений) по пространственной координате х и по времени t. Второй порядок по времени обеспечивался привлечением схемы Рунге - Кутты. При заданных f ° (отношении площади критического сечения сопла к площади поперечного сечения ДК), М0 и q° в течении периода работы ДК PDE отношение скоростей Ve/V0 получается как функция времени. Его интегрирование по периоду дает средние значения Ve/V0 и тяговые характеристики с учетом нестационарности и неизэнтропичности течения продуктов сгорания в детонационной камере.
На рисунке приведены кривые отношений Ve/V0 для ПВРД (цикл Брайтона, от времени не зависит) и для PDE: посчитанных по идеальному термическому кпд (PDEth) и для нескольких значений f °, найденных в рамках описанной выше нестационарной модели. Видно, что в типичных ситуациях ПВРД лучше многокамерных PDE с вращающимся клапаном (для f °= 0.3 и 0.1 – при М0 ³ 2 и М0 ³ 3). Согласно [3] тяговые характеристики ПВРД заведомо лучше тяговых характеристик и однокамерного PDE, предложенного в [4]. По этим характеристикам уступают ПВРД и все рассмотренные выше ВРД с горением в стационарных ДВ. Из еще не рассмотренных "детонационных" ВРД в последнее время особое внимание уделяется двигателям с вращающейся или спиновой ДВ (RDE). Одно из объяснений такого внимания – переход к стационарному течению во вращающейся со скоростью ДВ системе координат и последующие рассуждения с сохраняющейся в стационарных потоках полной энтальпией. При этом, правда, забывают, что в координатах, вращающихся с угловой скоростью w, вдоль линий тока сохраняется не "обычная" полная энтальпия H, а разность H °= H – (wr)2/2. В кольцевой камере сгорания RDE произведение wr равно скорости детонационной волны. Поэтому величина w так велика, что любые изменения радиальной координаты r при истечении продуктов сгорания заведомо исключают возможность определения отношения Ve/V0 через hth ВРД с ДГ. В противоположность этому, в силу сохранения H удельный импульс Isp RDE с сужающимся центральным телом и цилиндрической "внешней" образующей сопла заметно уменьшится. То что это так, подтверждают низкие значения Isp, рассчитанные в [5] для четырех вариантов RDE, летящих с М0 = 5 в однородной стехиометрической смеси водорода и воздуха с параметрами атмосферы Земли на высоте 20 км. Эти значения Isp = 1990, 2350, 2300 и 2250 с "традиционно" для авторов [5] (см. [3]) завышены: определяя Isp, они почему-то не учитывают сопротивления наветренной части центрального тела воздухозаборника. Исправленные значения Isp близки к 1420, 1830, 1780 и 1720 с, однако даже завышенные величины Isp заметно меньше Isp ПВРД, который при тех же условиях по оценке авторов [3] равен 3500¸3900 с. Дополнительное возрастание энтропии в RDE также имеет место – в УВ, примыкающей к ДВ на границе свежей горючей смеси и продуктов сгорания. Правда, интенсивность этой УВ невелика.
Итак, утверждения о возможном увеличении тяговых характеристик ВРД на десятки процентов благодаря использованию ДГ необоснованны. Даже для дозвуковых и малых сверхзвуковых чисел Маха полета, на которых ВРД с МГ может по тяговым характеристикам уступать PDE, последние заведомо уступают ТРД с МГ. Поэтому преимущества ВРД с ДГ, если и возможно, то не по тяговым характеристикам, а по простоте конструкции (как при малых М0 по сравнению с ТРД) или по меньшей теплонапряженности тракта двигателя (напротив, при больших сверхзвуковых числах Маха М0 > 5 в сравнении c пульсирующим детонационно-дефлаграционным двигателем [6]).
Работа выполнена при поддержке РФФИ (проект 17-01-00126).
Рисунок: кривые Ve/V0 ПВРД (цикл Брайтона) и PDE, рассчитанные по идеальному кпд (PDEth) и по нестационарной модели
1. Зельдович Я.Б. К вопросу об энергетическом использовании детонационного горения // ЖТФ. 1940. Т. 10. Вып. 17. С. 1453-1461.
2. Heiser W.H., Pratt D.T. Thermodynamic Cycle Analysis of Pulse Detonation Engines // J. of Propulsion and Power. 2002. V. 18. No. 1. P. 68-76.
3. Егорян А.Д., Крайко А.Н., Пьянков К.С., Тишин А.П. О расчете характеристик импульсного детонационного двигателя и их сравнении с характеристиками ПВРД // Теплофизика и аэромеханика. 2016. Т. 23. № 2. С. 307-310.
4. Remeev N.Kh., Vlasenko V.V., Khakimov R.A. Analysis of operation process and possible performance of the supersonic ramjet-type pulse detonation engine // Pulse and continuous detonation propulsion / Eds. G. Roy, S. Frolov. Moskow: TORUS PRESS, 2006. P. 235-250.
5. Дубровский А.В., Иванов В.С., Зангиев А.Э., Фролов С.М. Трехмерное численное моделирование характеристик прямоточной воздушно-реактивной силовой установки с непрерывно-детонационной камерой сгорания в условиях сверхзвукового полета // Химическая физика. 2016. Т. 35. № 6. С. 49-63.
6. Крайко А.Н., Александров В.Ю., Александров В.Г. и др. Способ организации горения топлива и детонационно-дефлаграционный пульсирующий прямоточный воздушно-реактивный двигатель. 2016. Патент РФ № 2585328.
Александр Николаевич Крайко
Кубанский государственный университет
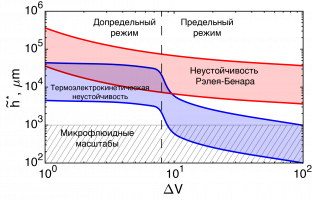
Работа посвящена теоретическому изучению термоэлектрокинетической неустойчивости. Данный тип неустойчивости возникает в электролите около ионоселективных поверхностей при учете Джоулева нагрева электролита вследствие прохождения через него электрического тока [1-3]. В результате линейного анализа устойчивости одномерного решения были обнаружены два типа неустойчивости, которые возникают при различных ориентациях канала относительно силы тяжести: Ra>0 для неустойчивости Рэлея-Бенара, Ra<0 для термоэлектрокинетической неустойчивости.
При малых разностях потенциалов, для допредельного режима, абсолютные величины критических значений числа Рэлея имеют одинаковые порядки. При увеличении разности потенциалов ∆V возникает режим предельных токов. Возникновение этого режима обусловлено появлением области пространственного заряда. Именно наличие зоны пространственного заряда является необходимым условием для возникновения классической электрокинетической неустойчивости. Как показывают расчеты, зона пространственного заряда никак не влияет на неустойчивость Рэлея–Бенара. Термоэлектрокинетическая неустойчивость же, напротив, непосредственно связана с проводимостью электролита и наличием объемного заряда, которое порождает скорость электроосмотического скольжения на границе с зоной пространственного заряда. Наличие скорости скольжения действует в совместно с термоэлектрокинетическим конвективным движением, поэтому критическое число Рэлея существенно уменьшается.
Для режима предельных токов критические числа Рэлея для термоэлектрокинетической неустойчивости уменьшаются в тысячи раз, что делает их физически возможными в микронных масштабах. В то же время критические числа Рэлея для неустойчивости Рэлея–Бенара имеют, по сути, тот же порядок, что и для режимов допредельных токов, это подтверждает устоявшееся мнение, что в задачах микрофлюидики неустойчивость Рэлея–Бенара не проявляется.
Работа выполнена при частичной финансовой поддержке РФФИ 18-38-00611-мол_а и Министерства образования и науки Краснодарского края, проект № 16-48-230107-р_а.
Наталья Юрьевна Ганченко
Пермский государственный национальный исследовательский университет
В проведенном исследовании экспериментальными и численными методами изучен механизм развития теплового и гидродинамического пограничных слоев вблизи нагретых пластин различной форм и размеров. В частности, исследованы пространственная периодичность и временная эволюция локальных конвективных потоков в жидкости. Рассмотрены вопросы устойчивости пограничного слоя на этапе формирования конвективного факела.
Визуализация течения выполнялась при помощи флуоресцирующего красителя, в качестве которого использовался родамин. При появлении в полости конвективного течения красящее вещество поднималось вверх, позволяя наблюдать структуру потока. На рисунке справа изображены фотографии течений над нагревателем различной формы в плоскости лазерного ножа с длиной волны 532 нм.
Лабораторные исследования проводились лишь для качественного представления реального процесса развития конвективного течения. С целью обобщения результатов наблюдений и исследования количественных характеристик более сложных течений выполнялось численное моделирование в пакете COMSOL. Основной результат исследования заключался в разработке теоретический модели, которая представляет собой комбинацию гармонических функций и позволяет описать структуру пограничного слоя исходя из граничных условий задачи.
Решение обсуждаемых в данной работе вопросов поможет лучше представлять механизмы передачи тепла от нагретых тел различной формы и способы организации конвективного течения в системах с локализованными источниками тепловыделения [1-3]. Кроме того, полученные результаты найдут применение в области проектирования современных систем охлаждения электронных устройств и компонентов, а также обеспечить научно обоснованный выбор оптимальных параметров геометрических размеров теплообменных поверхностей и неизотермических технологических процессов [4-7].
Работа выполнена при поддержке РФФИ (проект 18-31-00165 мол_а).
1.Гибанов Н.С., Шеремет М.А. Влияние формы и размеров локального источника энергии на режимы конвективного теплопереноса в квадратной полости // Компьютерные исследования и моделирование. 2015. Т. 7 № 2. С. 271–280.
2.Kaminski E. Rise of volcanic plumes to the stratosphere aided by penetrative convection above large lava flows // Earth and Planetary Science Letters. 2011. Vol. 301. P. 171–178.
3.Cagney N. et al. Temperature and velocity measurements of a rising thermal plume // Geochemistry, Geophysics, Geosystems. 2015. Vol. 16, no. 3. P. 579–599.
4.Lappa M. Some considerations about the symmetry and evolution of chaotic Rayleigh–Bénard convection: The flywheel mechanism and the “wind” of turbulence // Comptes Rendus Mécanique, 2011, Vol. 339, no. 9, P. 563–572.
5.Hattori T. et al. Prandtl number dependence and instability mechanism of the near-field flow in a planar thermal plume // J. Fluid Mech. 2013, Vol. 732, P. 105–127.
6.Keken P. E., Davaille A., Vatteville J. Dynamics of a laminar plume in a cavity: The influence of boundaries on the steady state stem structure // Geochemistry, Geophysics, Geosystems. 2013. Vol. 14, no. 1. P. 158–178. .
7.Kondrashov A., Sboev I., Dunaev P. Evolution of convective plumes adjacent to localized heat sources of various shapes // International Journal of Heat and Mass Transfer. 2016. Vol. 103. P. 298–304.
Иван Олегович Сбоев
НИИ механики МГУ им. М.В. Ломоносова
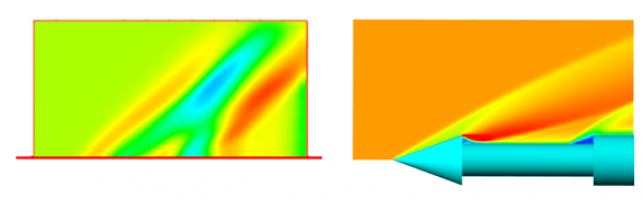
В рамках двухконтинуальной модели сжимаемого ламинарного пограничного слоя [1] исследуется продольное обтекание полубесконечной плоской теплоизолированной пластины сверхзвуковым газокапельным потоком. Массовая доля дисперсной фазы считается малой, но конечной. Рассматривается диапазон невысоких равновесных температур пластины, в котором испарением капель внутри пограничного слоя и на поверхности пластины можно пренебречь. Показано, что в заданных условиях необходимо учитывать неоднородность температуры вещества внутри капли. В межфазном обмене импульсом, помимо силы Стокса, учитывается подъемная сила Сэфмана [2], приводящая к осаждению капель на пластину и формированию тонкой жидкой пленки внутри пограничного слоя [3]. На основании параметрических численных расчетов исследованы распределения параметров фаз внутри пограничного слоя и равновесной температуры вдоль поверхности пластины. Показано, что снижение температуры обтекаемой поверхности напрямую зависит от величины силы Сэфмана, а также, что даже при небольших (порядка процента) массовых концентрациях капель в набегающем потоке равновесная температура стенки может понизиться на десятки градусов (Рис.1). Данное обстоятельство делает возможным использование примеси жидких капель в перспективных системах безмашинного энергоразделения газовых потоков [4].
Работа выполнена при финансовой поддержке РНФ (проект № 14-19-00699).
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Osiptsov A.N. Mathematical modeling of dusty-gas boundary layers// Appl. Mech. Rev. 1997. V. 50. P. 357-370.
2. Saffman P.G. The lift on a small sphere in a slow shear flow// J. Fluid Mech. 1965. V. 22. P. 385. Corrigendum: J. Fluid Mech. 1968. V. 31. P. 628.
3. Осипцов А.Н., Шапиро Е.Г. Обтекание поверхности аэродисперсным потоком с образованием жидкой плёнки из осаждающихся частиц// Изв. АН СССР. Механика жидкости и газа. 1989. № 4. С. 85-92.
Леонтьев А.И. Газодинамический метод энергоразделения газовых потоков// Теплофизика высоких температур. 1997. Т. 35, № 1. С. 157.
Ирина Валерьевна Голубкина
ФИАН им. П.Н. Лебедева

Известно, что турбулентность характеризуется перемежаемостью, что проявляется, в частности, в развитии неизотропных нестационарных интенсивных мелкомасштабных вихревых структур [1]. В работе показано, что исходя из общих уравнений динамики жидкости, можно дать количественные оценки явлению раскручивания и вытягивания небольших жидких частиц из инерционного интервала изотропной турбулентности. Само явление, названное ранее пируэт-эффектом [2], раскрывает механизм образования интенсивных структур в мелкомасштабной турбулентности. На основании [3] в работе построена линейная стохастическая лагранжева модель, в которой получено кинетическое уравнение на функцию распределения квадрата косинуса угла между завихренностью и собственным вектором тензора скоростей деформации жидкой частицы, а также аналитически посчитаны асимптотики зависимости от времени этой величины при больших и малых временах [4]. Результаты находятся в хорошем согласии с результатами проведенных ранее экспериментов и численных расчетов [2, 5]. Проведенный анализ показывает, что линейные процессы, возможно, играют основную роль в некоторых процессах принципиально нелинейного явления изотропной турбулентности.
Важность представленных результатов заключается в самом факте применимости линейной стохастической модели в принципиально нелинейном процессе турбулентности. Показано, что линейные эффекты возможно играют главную роль в пируэт-эффекте, который раскрывает механизм образования интенсивных вихревых структур в мелкомасштабной турбулентности.
Исследование выполнено во ФГУП «Центральный аэрогидродинамический институт имени профессора Н.Е. Жуковского» за счет гранта Российского научного фонда (проект №17-11-01271)
1. Кузнецов В.Р., Сабельников В.А. Турбулентность и горение, М: Наука, 1986, 288 с.
2. Xu H., Pumir A., Bodenschatz E. The pirouette effect in turbulent flows // Nat. Phys., 2011, 7, 709.
3. Зыбин К.П., Сирота В.А., Ильин А.С., Гуревич А.В. Генерация мелкомасштабных структур в развитой турбулентности // ЖЭТФ, 2007, 132, 2 (8), 510-523.
4. Зыбин К.П., Копьев А.В. Теоретическая модель возникновения вихревых структур в изотропном турбулентном потоке, основанная на линейном механизме // Изв. РАН. МЖГ, 2018, 4, в печати.
5. Pumir A., Bodenschatz E., Xu H. Tetrahedron deformation and alignment of perceived vorticity and strain in a turbulent flow // Phys. Fluids, 2013, 25, 035101
Алексей Викторович Копьев
Пермский Государственный Гуманитарно-Педагогический Университет

Исследуется влияние круговых поступательных вибраций на тепловую конвекцию в тонком горизонтальном плоском слое с изотермическими границами различной температуры. Плоский слой подогревается сверху и совершает поляризованные по кругу вибрации в горизонтальной плоскости. Изучена граница возбуждения вибрационной тепловой конвекции в устойчиво стратифицированной в поле силы тяжести жидкости в зависимости от интенсивности вибраций, толщины слоя и разности температур границ слоя. Результаты исследований представлены на плоскости управляющих безразмерных параметров, гравитационного и вибрационного чисел Релея. Эксперименты выполнены на тонких слоях воды, а также этилового спирта. Случай вращающегося плоского слоя в осциллирующих силовых полях при равенстве частоты осцилляций и частоты вращения ранее был рассмотрен в работе [1].Обнаружено повышение теплопереноса существенно ниже порога возбуждения «классической» вибрационной конвекции. Наблюдения показали, что в слое развивается система конвективных ячеек (см.рис.). Возрастание теплового потока наблюдается в ограниченной области частот. Предполагается, что развитие ячеистой вибрационной тепловой конвекции связано с возбуждением собственных колебаний устойчиво стратифицированной в поле силы тяжести жидкости. При высокочастотном вибрационном воздействии порог возбуждения тепловой конвекции близок к теоретически исследованному.
Работа выполнена в рамках в рамках задания Минобрнауки (проект РФ 3.9053.2017/БЧ).
1. Вяткин А.А., Иванова А.А., Козлов В.Г., Рысин К.Ю. Влияние тангенциальной составляющей силового поля на конвекцию во вращающемся плоском слое // Изв. РАН. Физика атмосферы и океана, 2017, том 53. № 2. С. 215–222.
Кирилл Юрьевич Рысин
НИИ механики МГУ им. М.В. Ломоносова
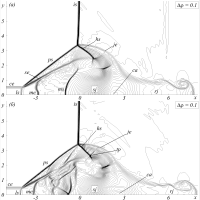
Эффект сильной перестройки фронта ударной волны, распространяющейся по ударной трубе, известен с 1954 года [1]. Аналогичное явление имеет место при распространении ударных волн от мощных взрывов [2]. Приповерхностный участок фронта волны обгоняет основной фронт волны, при этом формируется косая ударная волна, распространяющаяся по невозмущенному газу вдали от стенки. Ударно-волновая структура, обгоняющая основной фронт волны, получила название «предвестник». Перестройка течения обусловлена взаимодействием набегающей ударной волны с тонким слоем горячего газа, возникающим вблизи поверхности при прогреве последней излучением фронта волны. Подобный эффект крупномасштабной перестройки течения при наличии тонкой «тепловой иглы» лежит в основе идеи снижения волнового сопротивления затупленных тел при помощи локального энерговклада в набегающий сверхзвуковой поток [3]. Согласно предположению [4], с некоторого момента времени предвестник растет линейно и почти автомодельно, однако в [5] было показано, что на больших временных интервалах линейный характер роста нарушается за счет эффекта «запирания потока» и развития неустойчивостей внутри предвестника.
В настоящей работе на основе уравнений Эйлера численно исследуется трехмерная задача о взаимодействии ударной волны с продольным каналом газа пониженной плотности круглого, эллипсоидального или прямоугольного сечения. Применяется численный метод WENO-Z [6] высокого порядка аппроксимации. Детально описана структура формирующегося предвестника и показано, что в трехмерном случае неустойчивости сдвиговых слоев внутри последнего развиваются быстрее, чем в осесимметричном течении. Определена зависимость скорости роста предвестника от формы сечения канала и обнаружено, что длительность участка линейного роста предвестника зависит в первую очередь от наибольшего линейного размера сечения канала.
Работа выполнена в НИИ механики МГУ им. М.В. Ломоносова с использованием ресурсов суперкомпьютерного комплекса МГУ им. М.В. Ломоносова при поддержке Российского фонда фундаментальных исследований (грант №18-01-00793).
(подпись к рисунку) Структура предвестника: изолинии плотности. (а) двумерное осесимметричное течение, (б) трехмерное течение для тех же параметров. ls – лидирующий скачок; ps, hs – боковой и внутренний скачки предвестника; se – преломленная граница канала; je – граница высоконапорной струи; sj и rj – прямая и возвратная осевые струи; ca – область кумуляции высоконапорной струи.
1. R.G. Shreffler, R.H. Christian Boundary Disturbances in High‐Explosive Shock Tubes// Journal of Applied Physics. 1954. V. 25. № 3. P. 324-331.
2. М.А. Садовский, В.В. Адушкин Влияние нагретого пристеночного слоя на параметры ударной волны // Доклады академии наук СССР. 1988. Т. 300. № 1. С. 79-83.
3. П.Ю. Георгиевский, В.А. Левин Сверхзвуковое обтекание тела при подводе тепла перед ним // Труды МИ АН СССР. 1989. Т. 186. С. 197-201.
4. В.И. Артемьев, И.Э. Маркович, И.В. Немчинов, В.А. Суляев Двумерное автомодельное движение сильной ударной волны над нагретой поверхностью // Доклады академии наук СССР. 1987. Т. 293. № 5. С. 1082-1084.
5. П.Ю. Георгиевский, В.А. Левин, О.Г. Сутырин Взаимодействие ударной волны с продольным слоем газа пониженной плотности // Изв. РАН. МЖГ. 2016. № 5. С. 125-132.
6. M.Castro, B. Costa, W.S. Don High order weighted essentially non-oscillatory WENO-Z schemes for hyperbolic conservation laws //Journal of Computational Physics. 2011. V. 230. №. 5. P. 1766-1792.
Олег Георгиевич Сутырин
Объединенный институт высоких температур Российской академии наук, Москва
Неустойчивость фронта пламени – одна из актуальных задач современной механики жидкости и газа. В зависимости от процессов, определяющих рост неоднородностей, для свободного сферического пламени различают гидродинамическую (Дарье-Ландау), термодиффузионную и неустойчивость Рэлея-Тейлора. Условиям для развития последней и посвящена данная работа.
Неустойчивость Рэлея-Тейлора возникает на границе раздела двух жидкостей или газов разной плотности при наличии ускорения, направленного от более легкого к тяжелому. При распространении пламени менее плотные разогретые продукты горения двигаются с ускорением в более плотном газе. Когда вектор ускорения и градиент плотности на фронте пламени сонаправлены, происходит развитие неустойчивости. Основным параметром, определяющим скорость развития этой неустойчивости, является число Атвуда. В ходе работы было рассчитано число Атвуда и обнаружено, что на границе раздела продуктов сгорания и горючей смеси оно зависит от начального содержания водорода.
Для исследования развития неустойчивостей была проведена серия экспериментов. Прозрачные латексные оболочки наполнялись предварительно подготовленной водородно-воздушной смесью. В различных сериях экспериментов менялось процентное содержание водорода. Инициирование пламени производилось искровым разрядом с энергией 1мДж, разрядником, расположенным в центре оболочки. Регистрация распространения фронта пламени производилось с использованием теневого метода реализованного в теневом приборе ИАБ-451 и высокоскоростной камеры ВидеоСпринт. Видеосъемка процесса производилась с частотой от 500 до 1000 кадров в секунду с экспозицией в 500 мкс. С целью автоматизации обработки полученных изображений в среде Matlab написана программа, преобразовывающая набор изображений расширяющегося фронта пламени в зависимость среднего радиуса от времени.
Обнаружено, что на начальной стадии распространения возникают как ускорения, так и замедления фронта пламени. Экспериментально полученные параметры распространения фронта пламени дополнены расчетами, проведенными по аналитической модели из литературы.
Работа выполнена при поддержке Российского Научного Фонда, грант №14-50-00124.
Артём Евгеньевич Ельянов
Уральский государственный университет путей сообщения
Рассмотрена полная система уравнений Навье-Стокса в случае одномерного плоско-симметричного течения вязкого теплопроводного сжимаемого газа, с независимыми термодинамическими параметрами δ=1/ρ – удельный объем, p – давление [1, 2]. Для неё поставлена начально-краевая задача c условием непротекания на границах x=0 и x=π и условием теплоизоляции на этих же границах.
Решение данной начально-краевой задачи представляется в виде бесконечных тригонометрических рядов. Чтобы получить уравнения для коэффициентов рядов, каждое уравнение системы проецируется на свою систему базисных гармоник. Из-за того, что эти коэффициенты зависят только от одной переменной, данной процедурой задача построения всего решения сводиться к решению бесконечной системы обыкновенных дифференциальных уравнений (СОДУ).
Чтобы численно построить решение полученной СОДУ, ограничиваем количество слагаемых рядов, а также упрощаем выражения в правых частях СОДУ, избавившись от двойных сумм. Данная СОДУ решается с помощью метода Рунге-Кутты 4-го порядка точности. После нахождения коэффициентов рядов, их значения подставляются в исходное представление решения.
Полученное решение полной системы уравнений Навье-Стокса совпадает с результатами предыдущих исследованиях полученными в [1].
1.Баутин С.П., Замыслов В.Е., Скачков П.П. Математическое моделирование тригонометрическими рядами одномерных течений вязкого теплопроводного газа. Новосибирск: Наука; Екатеринбург: Изд-во УрГУПС, 2014.
2.Баутин С.П. Характеристическая задача Коши и её приложения в газовой динамике. Новосибирск: Наука, 2009.
Екатерина Анатольевна Родина
Уральский Государственный Университет Путей Сообщения
Тропический циклон — тип циклона, или погодной системы низкого давления, что возникает над теплой водяной поверхностью и сопровождается мощными грозами, выпадением ливневых осадков и ветрами штормовой силы. Традиционно считается, что тропические циклоны получают энергию от поднятия влажного воздуха вверх, конденсации водяных паров в виде дождей и опускания более сухого воздуха вниз.
В книгах [1,2] предложена другая схема возникновения и функционирования тропических циклонов. Неравномерный локальный нагрев подстилающей поверхности приводит к появлению неоднородностей температуры, плотности и давления. При действии сил тяжести и Кориолиса это является причиной возникновения сложного нестационарного закрученного движения среды.
Для решения задачи о моделировании трехмерных нестационарных течений, имеющих место в тропических циклонах, предлагается строить решение полной системы дифференциальных уравнений Навье-Стокса, при действии сил тяжести и Кориолиса. Для численного моделирования таких течений используется метод конечных разностей с использованием явной разностной схемы.
1.Баутин С.П. Торнадо и сила Кориолиса. Новосибирск: Наука, 2008.
2.Баутин С.П., Дерябин С.Л., Крутова И.Ю., Обухов А.Г. Разрушительные атмосферные вихри и вращение Земли вокруг своей оси. Екатеринбург: Изд-во УрГУПС, 2017.
Юлия Анатольевна Агеева
НИИ механики МГУ имени М.В. Ломоносова, Москва/ ООО "Тесис", Москва
Сверхзвуковое обтекание элементов конструкции потоком газа может иметь сложную и неоднозначную структуру из-за наличия отрывных областей и скачков уплотнения. В ряде случаев возможен гистерезис, проявляющийся в зависимости итоговой картины течения от предыстории его развития. В области гистерезиса при одних и тех же физических параметрах и граничных условиях могут реализовываться различные устойчивые картины обтекания.
Важной особенностью течений с гистерезисом является то, что при внесении в области гистерезиса разового возмущения нужной мощности структура течения изменяется и не возвращается к предшествующей структуре после исчезновения возмущения.
Работа посвящена исследованию управления потоком в условиях гистерезиса. Исследования проводятся с использованием численного моделирования в программных комплексах Abaqus и FlowVision на двух задачах: колебании упругой пластины в сверхзвуковом потоке и сверхзвуковом обтекании осесимметричного тела с кольцевой каверной.
Колебания упругой пластины можно условно разделить на три основных вида: простой одномодовый флаттер с одной независимой частотой, резонансный флаттер с двумя кратными частотами и непериодический флаттер с двумя или более некратными частотами. Гистерезис реализуется в области резонансного и непериодического флаттеров, содержащих более одной независимой частоты [1]. Внесение кратковременного возмущения в области гистерезиса приводит к развитию колебаний другого вида.
Течение в кольцевой каверне осесимметричного тела при сверхзвуковом обтекании может быть двух видов: с открытым и замкнутым режимами [2]. На определенном интервале соотношений между длиной и глубиной каверны в зависимости от предыстории реализуются либо замкнутый, либо открытый режим. При наличии каверны сопротивление обтекаемого тела с замкнутым режимом течения в каверне может существенно превышать сопротивление аналогичного тела с открытым режимом течения. Внесение кратковременного возмущения в уже сформировавшееся течение позволяет изменить режим течения в каверне и тем самым увеличить или уменьшить сопротивление тела.
Исследования проводились в рамках проекта РФФИ 18-01-00404 и госбюджетных тем АААА-А16-116021110201-2 и АААА-А16-116021110196-1 НИИ механики МГУ (http://www.imec.msu.ru).
1. Shishaeva A. S., Vedeneev V. V., Aksenov A. A., Sushko G. В.. Transonic panel flutter in accelerating or decelerating flow conditions// AIAA Journal, 2018, V. 56(3), P. 1-14.
2. Шишаева А. С., Симоненко М. М., Гувернюк С. В., Аксенов А. А.. Численное моделирование аэродинамического гистерезиса при сверхзвуковом обтекании осесимметричного тела с каверной в программном комплексе flowvision. // Физико-химическая кинетика в газовой динамике, 2017, Т. 18(1).
Анастасия Сергеевна Шишаева
НИИ механики МГУ
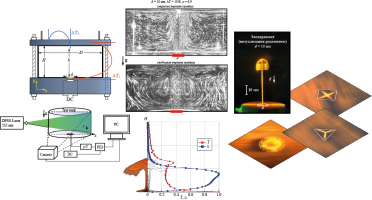
Было создано компактное устройство, формирующее воздушную струю диаметром 0.12 м, которая остается ламинарной на расстоянии 5.5 диаметров от выхода из формирующего устройства при числах Рейнольдса около 10000 [1].
Первым этапом настоящей работы является теоретическое исследование развития малых возмущений в струе с профилями скорости, соответствующими экспериментальным в начальном сечении струи и нескольких сечениях, близких к началу струи. Пространственный анализ устойчивости показал, что существует две ветви растущих возмущений: первая ветвь порождается точками перегиба на профилях скорости, расположенными вблизи границы струи; вторая — точкой перегиба, расположенной недалеко от оси струи. При этом скорости роста возмущений, соответствующих первой ветви, значительно больше скоростей роста возмущений, соответствующих второй ветви. Однако, с удалением от выхода из формирующего устройства, возмущения, соответствующие первой ветви, становятся затухающими (происходит слияние двух точек перегиба на профиле скорости в одну). Тогда неустойчивость продолжает порождаться только второй ветвью. Диапазон частот растущих возмущений для обеих ветвей одинаков и соответствует частотам 0…14 Гц. Частоты наиболее быстро растущих возмущений для обеих ветвей также лежат в одинаковом интервале — от 4 до 6 Гц.
Достаточно большой диаметр и длинный ламинарный участок струи, создаваемой экспериментально, позволяют детально измерять характеристики течения и визуализировать его. Были проведены эксперименты по внесению в струю возмущений посредствам колеблющейся с заданной частотой и фиксированной амплитудой проволоки. Визуализация течения показала, что при частотах, соответствующих теоретически полученному диапазону наиболее быстро растущих возмущений, струя разрушается ближе к выходу из формирующего устройства, чем при воздействии на струю возмущениями с частотами вне указанного диапазона. Были вычислены длины волн, возникающих в струе под воздействием возмущений, вызываемых колеблющейся проволокой. Эти длины волн хорошо коррелируют с длинами волн, полученными теоретически.
Исследование является первым шагом в экспериментальном изучении развития неустойчивости в затопленной струе круглого поперечного сечения и сравнении результатов с предсказаниями модальной теории устойчивости.
Работа поддержана РФФИ, проект №18-38-00745.
На рисунке - Схема устройства для внесения возмущений в струю и системы визуализации потока. Фотографии струи под воздействием возмущений с частотами 5 и 10 Гц.
[1] J. Zayko, S. Teplovodskii, A. Chicherina, V. Vedeneev, and A. Reshmin. Formation of free round jets with long laminar regions at large Reynolds numbers. 2018. Physics of Fluids, 30, 043603.
Олег Олегович Иванов
Пермский государственный национальный исследовательский университет
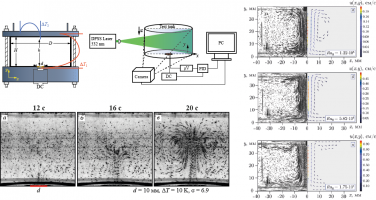
В ходе работы исследованы характеристики стационарного конвективного течения жидкости в цилиндрической полости, вызванного локализованным подогревом нижней границы. Опыты проводились с цилиндрическим слоем, у которого соотношение высоты к диаметру составляет H/D = 1 и 3 (рисунок). Высота рабочего слоя выбиралась равной 40 мм. Снизу полость ограничивалась массивом из оргстекла толщиной 25 мм, а сверху – алюминиевой пластиной толщиной 7 мм, либо оставалась открытой. С боковых сторон слой жидкости окружался трубкой из оргстекла с толщиной стенок 3 мм. Прозрачность боковой границы позволила исследовать структуру конвективных движений методом PIV. Для этого в рабочую полость, заполненную дистиллированной водой (0.97 г/см3), вносились светоотражающие частицы (1.05 г/см3), а при помощи вертикального лазерного ножа с длиной волны 532 нм вырезалась плоскость в центре слоя. Подогрев выполнялся за счет медного нагревателя диаметром d = 10 мм, расположенного в центре нижнего основания. С внутренней стороны медный теплообменник приводился в контакт с резистором. Для измерения температуры нагревателя ΔT1 внутри источника располагался спай дифференциальной термопары. Интенсивность подогрева поддерживалась постоянной за счет регуляции мощности тока, проходящего через резистор.
Имеющиеся результаты в виде термограмм ΔT2(t), зарегистрированных второй термопарой на высоте h = 37 мм над источником тепла, позволяют судить о длительности распространения теплового возмущения после включения источника тепла. Такой подход позволил исследовать зависимость времени достижения всплывающим конвективным факелом от степени подогрева. Однако существенное ограничение результатов этих исследований заключается в том, что, используя лишь сигнал термопары, нельзя получить представление о распространении факела раньше, чем он достигнет датчика температуры. Поэтому в ходе проведенного исследования уточнялась предлагаемая модель для скорости распространения конвективного факела [1]. Для этого применялась визуализация течения, которая позволила оценить продолжительность формирования конвективного течения и получить поправку для скорости распространения конвективной струи. Вместе с этим были исследованы характеристики установившегося течения при различных значениях управляющего параметра, в качестве которого использовалось число Рэлея Ra, а также для полостей с разным аспектным соотношением и граничными условиями на верхней стенке [2]. Кроме этого, на основе известной модели эволюции конвективного факела предприняты попытки обобщить теорию на случай течения в периодически изменяющемся инерционном поле.
Работа выполнена при поддержке РФФИ (проект 18-31-00165 мол_а).
1.Бабушкин И.А. и др. Развитие теплового плюма в узком вертикальном слое // Вестник ТГУ. Математика и механика. 2015. Т. 2, № 34. С. 41–52
2.Aminossadat S.M., Ghasemi B. A numerical study of mixed convection in a horizontal channel with a discrete heat source in an open cavity // European Journal of Mechanics - B/Fluids. 2009. Vol. 28, no. 4, P. 590–598
Иван Олегович Сбоев