НИИ механики МГУ
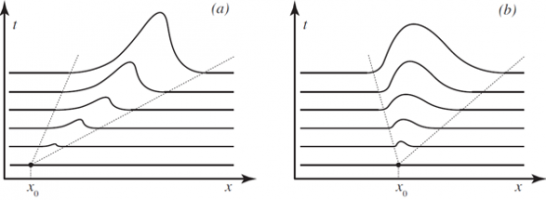
Абсолютный или конвективный характер неустойчивости сдвиговых течений оказывает большое влияние на развитие возмущений, в том числе на возможность реализации ламинарных течений на практике. Неустойчивость в однонаправленных затопленных струях, вызванная точкой перегиба в профиле скорости, обычно считается конвективной, хотя строго это было доказано лишь для одного конкретного семейства профилей как для плоских [1], так и для круглых [2] струй. Недавно в невязком приближении было показано [3], что существуют условия, в которых неустойчивость круглой струи без возвратного течения становится абсолютной. А именно, были установлены два фактора, управляющих характером неустойчивости – величина скорости в точке перегиба профиля скорости и «крутизна» профиля скорости в точке перегиба – и продемонстрирован профиль скорости, в котором сочетание этих факторов приводит к смене конвективного характера неустойчивости на абсолютный.
В настоящей работе этот вопрос исследуется с учётом вязкости. В плоскопараллельном приближении исследуется плоская затопленная струя несжимаемой жидкости, задаваемая профилем осевой скорости U(y). Рассматривается семейство параметризованных профилей, обеспечивающее гладкий переход от “классического” профиля скорости с единственной точкой перегиба, скорость в которой равна половине максимальной скорости, к профилю скорости, неустойчивость которого в невязком приближении абсолютна. Численным решение задачи на собственные значения для уравнения Рэлея (в невязком приближении) или Орра-Зоммерфельда (с учётом вязкости) анализируется положение седловой точки в комплексной плоскости функции ω(α), где ω – комплексная частота, α – комплексное волновое число. На первом этапе продемонстрировано, как в невязком приближении происходит движение седловой точки при гладкой деформации профиля скорости и, соответственно, смена конвективного характера неустойчивости на абсолютный.
На втором этапе для профилей скорости, абсолютно неустойчивых в невязком приближении, показано, что с учётом вязкости неустойчивость снова становится конвективной, если число Рейнольдса ниже некоторого критического значения. Найдена зависимость этого критического числа Рейнольдса от профиля скорости и показано, что оно может быть достаточно низким, при котором в экспериментах наблюдаются ламинарные участки струй. Обсуждаются возможные способы создания абсолютно неустойчивых струй и их возможные применения в технике.
Работа поддержана грантом РНФ № 20-19-00404.
1. Huerre P., Monkewitz P.A. Absolute and convective instabilities in free shear layers // J. Fluid Mech. 1985. V.159. P. 151-168.
2. Abid M, Brachet M, Huerre P. Linear hydrodynamic instability of circular jets with thin shear layers // Eur. J. Mech. B/Fluids. 1993. V.12(5). P. 683-693.
3. V. Vedeneev, J. Zayko. On absolute instability of free jets // Journal of Physics: Confer-ence Series. 2018. Vol. 1129. 012037.
Василий Владимирович Веденеев
НИИ механики МГУ
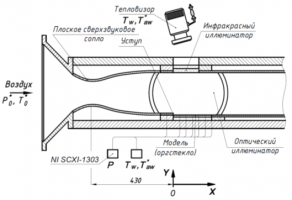
Одним из наиболее распространенных критериев оценки теплогидравлической эффективности каналов и трактов теплообменного и энергетического оборудования является коэффициент аналогии Рейнольдса – отношение коэффициента теплоотдачи, определяющего интенсивность теплообмена, к коэффициенту сопротивления, определяющего суммарные потери давления. Практически во всех методах интенсификации теплообмена (поверхностные турбулизаторы в виде ребер, штырьков, спиралей, вихревых камер и т.п.) коэффициент аналогии Рейнольдса снижается по сравнению с течением без интенсификаторов. Однако существуют отдельные перспективные способы интенсификации теплообмена, в которых наблюдается обратная тенденция опережающего роста теплообмена по сравнению с увеличением сопротивления: течение с положительным градиентом давления [1], использование вихреобразующего рельефа, формирование областей отрыва пограничного слоя и областей взаимодействия скачков уплотнения с пограничным слоем [2]. В данной работе внимание сконцентрировано на исследовании аналогии Рейнольдса в отрывной области сверхзвукового потока.
Исследование проводилось на сверхзвуковом аэродинамическом стенде АР-2 с использованием систем регистрации данных National Instruments, автоматизированных программ опроса и обработки показаний датчиков в среде LabView, термопар с термокомпенсацией, тепловизора и методов визуализации с помощью теневого прибора Теплера [3]. Число Маха набегающего потока варьировалось в диапазоне 2.0-3.0, температура торможения составляла около 293 К, число Рейнольдса, рассчитанное по длине динамического пограничного слоя от горла сопла, не менее 2·107.
1.Kiselev N.A., Leontiev A.I., Vinogradov Y.A., Zditovets A.G., Popovich S.S. Heat transfer and skin-friction in a turbulent boundary layer under a non-equilibrium longitudinal adverse pressure gradient // International Journal of Heat and Fluid Flow. 2021. Vol. 89. P. 108801.
2.Leontiev A.I., Popovich S.S., Vinogradov U.A., Strongin M.M. Experimental research of supersonic aerodynamic cooling effect and its application for energy separation efficiency // Proceedings of the 16th International Heat Transfer Conference, IHTC-16. 2018. V. 212244. 8 p.
3.Попович С.С. Особенности автоматизации эксперимента и обработки результатов при исследовании теплообмена в сверхзвуковом потоке сжимаемого газа // Программная инженерия. 2018. № 1. С. 35–45.
Сергей Станиславович Попович
Пермский национальный исследовательский политехнический университет
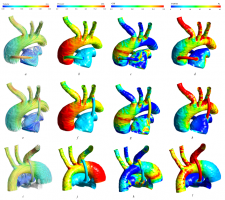
Показатели детской смертности у детей с врожденным пороком сердца неуклонно растут в России. Обструктивные поражения выводного тракта правого желудочка, изолированные или сочетающиеся с другими врожденными пороками сердца, составляют 25–30% врожденных аномалий сердца [1]. Хирургическое вмешательство является основным методом лечения нарушений развития сердечно – сосудистых структур при врожденных пороках сердца. Прорывным решением в хирургическом лечении цианотических врожденных пороков сердца оказалось создание модифицированного шунта Blalock–Taussig. Однако, хирурги встречаются с множеством факторов, влияющих на успешность операции, для анализа которых необходимо математическое моделирование и методы биомеханики [2]. В данной работе рассмотрена модель течения крови системы «аорта – шунт – легочная артерия» реального пациента с учетом взаимодействия «жидкость – твердое тело». Было проанализировано влияние анизотропной гиперупругой (Хольцапфеля–Гассера–Огдена) и изотропной гиперупругой моделей материалов аорты и легочной артерии, а также изотропной линейно – упругой и изотропной гиперупругой моделей материалов шунтов на значения гемодинамических параметров. Было выявлено, что модели материалов, как аорты и легочной артерии, так и шунтов имеют незначительное влияние на характер распределения гемодинамических параметров. Однако количественные значения данных параметров различаются. Показано, что модели материалов имеют незначительное влияние на объёмный расход через поперечное сечение шунта. Гемодинамически значимым является лишь местоположение шунта.
Александр Рафаелович Хайрулин
Институт океанологии РАН им П.П.Ширшова
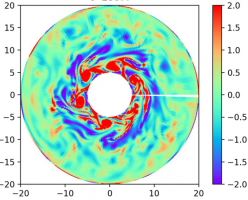
Преобразования энергии от крупномасштабных течений, вызываемых внешними воздействиями, являются объектом пристального внимания в силу важности приложений в геофизических, астрофизических и технических областях. Для планетарных систем в качестве внешнего воздействия могут выступать глобальные приливы, деформирующие жидкую оболочку. В частности, одним из важных проявлений являются крупномастшабные вихревые структуры типа волн Россби. Для выяснения базовых закономерностей формирования крупномасштабных структур в турбулентных режимах мы провели ряд численных и лабораторных экспериментов. Ранее [5,6] нами были выявлены закономерности аккумуляции волновой энергии во вращающихся слоях и механизмы потери устойчивости. При развитии нелинейных режимов возникает каскад триадных резонансов, приводящий к мелкомасштабным течениям и возникает обратный каскад, при котором возникают крупные (в терминах размеров слоя) вихревые структуры, медленно дрейфующие в азимутальном направлении. Таким образом, мы как численно, так и экспериментально получили преобразование симметрично поступающей механической энергии в азимутальный дрейф крупномасштабных вихревых структур. Проводится сопоставление полученных режимов с известными ранее теориями дрейфа крупномасштабных вихревых структур.
Ильяс Наилевич Сибгатуллин
НИИ механики МГУ, Москва
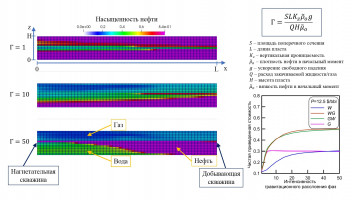
Исследуется влияние гравитационного расслоения фаз на оптимальные режимы водогазового воздействия на нефтяные пласты, предполагающего поочередную закачку воды и газа с целью вытеснения нефти. Целью данной работы является поиск безразмерного параметра, характеризующего гравитационное расслоение фаз, и исследование его влияния на коэффициент извлечения нефти и на значение чистой приведённой стоимости, характеризующей рентабельность водогазового воздействия. Для этого используется модель, объединяющая в себе физические и экономические параметры течения. Ранее рассматривалась аналогичная модель, описанная в [1], но для одномерного течения. В данной работе исследуются влияние стратификации фаз на оптимальные режимы водогазового воздействия.
Рассматривается двумерная модель нефтяного пласта заданной длины и высоты. На левой и правой границах расположены нагнетающая и добывающая скважины соответственно. В данной работе рассматриваются различные интервалы перфораций скважин и несколько различных режимов поочередной закачки смеси воды и углекислого газа. Параметр, характеризующий гравитационное расслоение фаз, выводится из системы уравнений, состоящей из законов сохранения массы каждой компоненты и закона Дарси. Исследуется влияние данного параметра на чистую приведённую стоимость закачки. Также рассмотрено несколько различных интервалов перфорирования скважин и исследовано их влияние на коэффициент извлечения нефти и чистую приведённую стоимость при различных значениях параметра подобия, характеризующего стратификацию фаз.
1. Afanasyev A., Andreeva A., Chernova A. Influence of oil field production life on optimal CO2 flooding strategies: Insight from the microscopic displacement efficiency // Journal of Petroleum Science and Engineering. 2021. V. 205. P. 108803
Анна Александровна Чернова
НИИ Механики МГУ
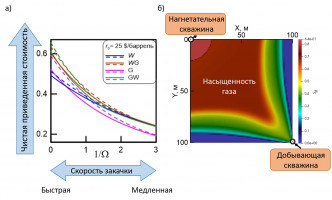
Для повышения нефтеотдачи пластов применяют различные методы, к примеру, закачка воды и газа. В статье [1] с использованием одномерной модели проведено исследование оптимальных режимов газового воздействия на нефтяные пласты с целью повышения нефтеотдачи и захоронения углекислого газа. Однако, реальные течения в пласте трехмерные, поэтому для более надежного описания фильтрации нужно использовать более сложные двух- и трех- мерные модели. Но так как увеличение размерности влечет увеличение сложности вычислений, то рассмотрим только двумерную модель в плоскости Oxy. Цель этого исследования понять, как меняется эффективная стратегия при переходе от одномерного течения к двумерному и насколько оправдано использование одномерной модели.
Закачка газа и/или воды проводится через нагнетательную скважину, расположенную в точке с координатами (0,0) (рис.). Рядом с нагнетательной скважиной фронт вытеснения распространяется осесимметрично при малых временах закачки. Далее, при приближении к добывающей скважине (100,100) фронт вытягивается, оставляя неохваченными области рядом с границами X=100 и Y=100. Коэффициент охвата нефти в этом случае меньше единицы. В одномерном случае, когда вытеснением охвачен весь объем породы, коэффициент охвата равен единице. Так значения чистой приведенной стоимости (NPV), соответствующие случаю 2-D, всегда ниже значений, соответствующих 1-D случаю. Но области оптимальных стратегий закачки качественно совпадают в 1-D и 2-D постановках задачи.
Анна Игоревна Андреева
Институт механики и машиностроения ФИЦ КазНЦ РАН
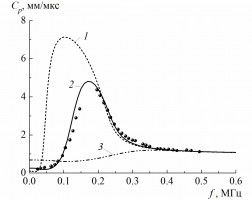
Покрытые вязкоупругой оболочкой пузырьки встречаются во многих областях. Но основное применение они нашли в биомедицине, где используются в качестве контрастных веществ для ультразвуковой диагностики [1]. В рамках данной работы получено модифицированное уравнение Релея-Ламба, учитывающее радиальные колебания пузырька газа, покрытого вязкоупругой оболочкой и находящегося в вязкоупругой среде. Учет вязкоупругости оболочки и несущей жидкости проводится на основе реологических моделей Кельвина-Фойгта и Максвелла. Для случая малых возмущений найдено дисперсионное уравнение, учитывающее межфазный теплообмен межу газом, вязкоупругой оболочкой и несущей средой. Проиллюстрировано влияние оболочки пузырьков, упругости несущей фазы на динамику акустических волн. В частности, на приведенном рисунке представлено влияние упругости несущей среды, оболочки пузырьков на зависимости фазовой скорости от частоты возмущений для смеси полидиметилсилоксана (PDMS RTV-615) с воздушными пузырьками. Дано сравнение теории с экспериментальными данными [2]. Параметры расчета и математическая модель представлены в работах [3, 4]. Кривая 1 построена без учета упругости несущей среды, кривая 2 – с учетом упругости несущей среды, кривая 3 – с учетом упругости несущей среды и при наличии вязкоупругой оболочки пузырьков. Как видно из рисунка, учет упругости несущей фазы приводит к сдвигу резонансной частоты возмущений (кривая 2), что также хорошо подтверждается экспериментальными данными. Дополнительный учет вязкоупругой оболочки приводит к еще большему значению резонансной частоты (кривая 3). Наличие оболочки пузырьков может привести также к исчезновению полосы непрозрачности у фазовой скорости (фазовая скорость не превысит скорость звука в несущей фазе во всем диапазоне частот). Это связано с тем, что оболочка пузырьков сдерживает пульсации включений. Пузырьки ведут себя как твердые частицы и, в связи с этим, происходит меньшее рассеяние акустической волны по сравнению с обычными пузырьковыми средами.
1.Goldberg B.B., Raichlen J.S., Editors F.F. Ultrasound contrast agents. Basic principles and clinical applications. Martin Dunitz, 2001.
2. Leroy V., Strybulevich A., Page J.H., Scanlon M. G. Influence of positional correlations on the propagation of waves in a complex medium with polydisperse resonant scatterers // Physical Review E. 2011. V. 83. P. 046605.
3. Губайдуллин Д.А., Федоров Ю.В. Волновая динамика покрытых оболочкой включений в вязкоупругой среде // ПМТФ. 2020. Т. 61. № 4. С. 22-30.
4. Gubaidullin D.A., Fedorov Yu.V. Acoustics of a viscoelastic medium with encapsulated bubbles // Journal of Hydrodynamics. 2021. V. 33. № 1. P. 55-62.
Юрий Валентинович Федоров
ПЕРМСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Производство кварцевых оптических волокон – сложное высокотехнологичное дорогостоящее производство, поэтому задача об оптимальном стабилизирующем управлении этим процессом является актуальной в течении уже нескольких десятилетий.
Численная реализация решения системы оптимальности для задачи оптимального управления процессом вытяжки кварцевых оптических волокон [1] проводилась с использованием метода конечных элементов в пакете мультифизического моделирования Comsol Multiphysics. Процесс решения данной системы можно разделить на нескольких этапов:
- поиск стационарного решения (функций , и );
- нахождение функций , , , , , , , , , , , зависящих от стационарных состояний;
- непосредственное решение системы оптимальности, а также отыскание функции оптимального управления;
- анализ полученных результатов.
Значения параметров, входящих в систему, описывающую процесс вытяжки оптических волокон, а также в систему оптимальности, представлены в [2]. Для решения системы оптимальности возмущение радиуса волокна от его стационарного состояния задавалось в виде, представленном на рис. 1. Максимальное отклонение радиуса волокна составило 2%. На рис. 2 представлена полученная функция управления . Ее максимальное значение +7%, что соответствует реальным возможностям производства. Для анализа эффективности управления были найдены функции отклонения радиуса готового волокна для двух разных режимов вытяжки (в точке ): без управления – сплошная линия 1 и с управлением – пунктирная линия 2 (рис. 3). Отметим, что процесс имеет тенденцию к стабилизации уже со 2 секунды, а концу 6 секунды – стабилизируется полностью, т.е. отклонение функции радиуса готового волокна равно нулю.
Ирина Викторовна Гордеева
НИИ механики МГУ
Движение по воде наземных транспортных средств вызывает большой интерес. Они не только являются амфибиями, то есть могут двигаться одновременно по воде и по суше, но и при движение по воде, значительно экономят топливо. В работе рассматривается машинка с гусеницей, которая оснащена грунт зацепами и при взаимодействии с водой создаёт тягу больше, чем колесо. Рассматривается плоскопараллельное движение и во всё время объект наклонён к горизонтальной поверхности под некоторым постоянным углом (в данной задаче рассматривались малые углы наклона). Таким образом, имеется две степени свободы – это координаты центра масс. Вертикальная указывает, насколько машинка погружена в воду, изменение горизонтальной координаты – линейную скорость. Эти два параметра будут основными, при изучении движения данного объекта.
На машинку действуют сила тяжести, подъёмная сила и сила сопротивления со стороны воды на её погруженную часть, а также тяга создаваемая гусеницей. В модели учитывается погружение машинки, это приводит к изменению сил, связанных с взаимодействием с водой. Тяга и подъёмная сила моделируются на основе данных экспериментов, которые проводились на водоканале НИИ механики МГУ. Дана оценка начальной скорости и угловой скорости вращения гусеницы, при которой машинка не будет тонуть. Приведены результаты моделирования и получен диапазон значений, при которых возможно движение по поверхности воды.
Андрей Петрович Голуб
Институт механики и машиностроения ФИЦ Казанский научный центр РАН
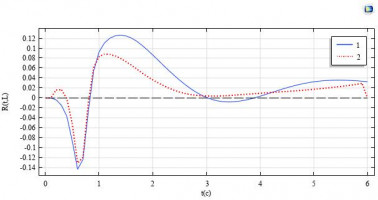
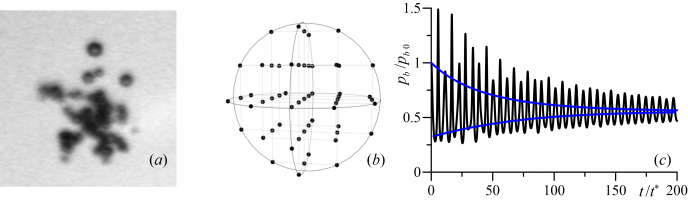
При достаточно больших концентрациях парогазовых пузырьков в жидкости значительную роль играет их гидродинамическое взаимодействие [1, 2]. В результате взаимодействия пузырьки могут сильнее расширяться и сжиматься, перемещаться по жидкости, образовывать кластеры (рис. а) и т.д. Эти и другие особенности взаимодействия пузырьков могут быть использованы в различных приложениях.
В настоящей работе изучается влияние взаимодействия между воздушными пузырьками в сферическом кластере (рис. b) в водоглицериновой смеси при мгновенном повышении их внутреннего давления. В экспериментах подобное повышение давления реализуется, например, при образовании пузырьков искровым или оптическим (лазерным) пробоем жидкости. До момента времени t=0 пузырьки и жидкость находятся в состоянии покоя, радиус пузырьков R0=0.25 мм, давление жидкости pL=1 бар, ее плотность rL=1156 кг/м3. Центры пузырьков расположены в узлах равномерной кубической сетки внутри сферической области так, что один из пузырьков располагается в центре этой области. Размер ячеек сетки 5 мм. При t=0 давление в пузырьках pb мгновенно повышается от равновесного значения pb0 до pb0+Dp, где Dp варьируется в диапазоне от 0.1 до 0.8 бар. Динамика пузырьков в кластере описывается системой ОДУ, представляющей собой частный случай уравнений работы [1].
Рис. (a) – фотография кластера пузырьков из эксперимента [2]; (b) – схема изучаемого кластера из 57 пузырьков; (c) – изменение безразмерного давления в центральном пузырьке кластера (черная кривая) и огибающие экстремальных значений давления в одиночном пузырьке (синие кривые), t*=R0(rL/pL)0.5.
Повышение давления в пузырьках приводит к возникновению их радиальных колебаний, которые постепенно затухают под влиянием сжимаемости и вязкости жидкости. В результате система со временем переходит в новое равновесное состояние. Процесс перехода в новое равновесное состояние пузырьков кластера во многом отличается от перехода одиночного пузырька, что обусловлено взаимодействием пузырьков. В частности, колебание давления в пузырьках кластера затухает существенно немонотонно (рис. c). При этом у пузырьков в кластере скорость затухания и частота колебаний давления значительно меньше, чем у одиночного пузырька. Максимальные давления в пузырьках центральной области кластера принимают значения, заметно превосходящие максимальное давление в одиночном пузырьке.
1. Aganin A.A., Davletshin A.I. Equations of interaction of weakly non-spherical gas bubbles in liquid // Lobachevskii Journal of Mathematics. 2018. V. 39. № 8. P. 1047-1052.
2. Luther S. Theoretische Beschreibung und experimentelle Untersuchung raum-zeitlicher Strukturbildung in akustischen Kavitationsblasenfeldern. – Niedersächsische Staats- und Universitätsbibliothek, 2000.
Анас Ильгизович Давлетшин
НИИ механики МГУ имени М.В. Ломоносова, Москва
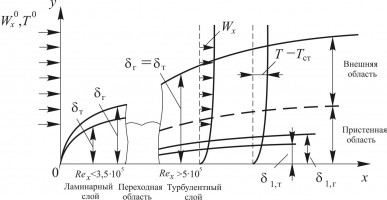
Установлены законы подобия для профилей скорости и температуры, справедливые в пристеночной области до- и сверхзвукового турбулентного пограничного слоя, которые позволяют представить профили скорости и температуры в потоке сжимаемого газа через профили этих величин в несжимаемом пограничном слое. Они получены как асимптотические разложения решения уравнений Рейнольдса по малому параметру – числу Маха, вычисленному по динамической скорости и энтальпии газа на стенке. Главный член разложения для профиля скорости соответствует известной формуле Ван Дриста. Однако полученное решение содержит еще дополнительные слагаемые порядка единицы, что объясняет расхождение формулы Ван Дриста с экспериментальными данными. Аналогичную структуру имеет закон стенки для температуры, который для сжимаемого течения сформулирован впервые.
Кроме постоянной Кармана и турбулентного числа Прандтля в логарифмической области, известных для течения несжимаемой жидкости, полученные соотношения содержат три новые универсальные константы, которые не зависят от молекулярных свойств и отношения теплоемкостей газа.
Работа выполнена при поддержке гранта Московского Центра фундаментальной и прикладной математики.
Алексей Игоревич Агеев
Институт механики сплошных сред УрО РАН
В процессе химического производства, в том числе минеральных удобрений возникает необходимость утилизации избыточных высокоминерализованных рассолов. Основным средством утилизации рассолов является сброс в поверхностные водные объекты или подземные водоносные горизонты. При этом при распространении насыщенного рассола в поверхностных водных объектах, происходит аккумуляция солей в грунтовых водах речного дна. Накопленные примеси в водоносном слое дна реки, безопасные при малых и средних расходах, с увеличением интенсивности течения реки в период половодья становятся интенсивным источником загрязнения, существенно органичивающим режим водопользования.
Работа посвящена трехмерному численному моделированию выноса примеси из дна реки. Расчетная область состояла из массива жидкости (реки), распространяющейся над пористой средой (дно реки). Проведены расчеты выноса, накопленных загрязнений в зависимости от гидрологического режима водоема-приемника. Численное моделирование транспорта примеси в двухслойной системе жидкость – пористая среда, насыщенная жидкостью, проводилось для параметров максимально приближенных к описанию течения, возникающего в естественных водных объектах. Промоделировано дальнейшее распространение шлейфа загрязняющих веществ.
Трехмерное численное моделирование турбулентных течений и массопереноса проводилось с использованием k-omega модели турбулентности с учетом плотностной стратификации, возникающей из-за наличия «тяжелых» примесей. Для дискретизации определяющих уравнений и граничных условий использовался метод конечных объемов.
Верхняя граница области, соответствующая свободной поверхности жидкости, считалась недеформируемой; на ней ставились условия отсутствия нормальной компоненты скорости и касательных напряжений, а также условие отсутствия потока примеси. На нижней и боковых границах расчетной области выполнялись условия равенства нулю производной скорости по нормали и отсутствия потока примеси. На входе расчетной области задавалась постоянная скорость течения и постоянная концентрация примеси. На выходе расчетной ставились «мягкие» граничные условия продолжения потока. На прочих границах задавались условия прилипания, и границы считались непроницаемыми для вещества. Для пространственной дискретизации уравнений использовалась схема второго порядка точности. Временная эволюция моделировалась по явной схеме второго порядка. Начальное распределение по глубине полагалось однородным. В результате проведения вычислений получены распределения концентрации рассола по глубине, получены критические параметры потока, при которых происходит залповый вынос загрязнений, исследован дальнейший характер распространения примеси.
Янина Николаевна Паршакова
Институт механики и машиностроения – обособленное структурное подразделение ФИЦ КазНЦ РАН
Воздействие волновых процессов на ограниченную многофазную среду приводит к возникновению нелинейных явлений [1]. В работе [2] рассматриваются резонаторы в виде конуса, рупора или колбы. Создаваемые колебания сильно влияют на поведение частиц в данных объемах [3]. Например, изменению поля средней температуры [4], усилению перемешивания [5], ускорению осаждения и увеличению теплообмена среды [6]. Ранее рассматривались осаждения частиц аэрозоля при резонансных колебаниях в трубах [7].
В данной работе исследуется динамика аэрозоля в резонаторе прямоугольного сечения вблизи резонансной частоты. Получены значения колебаний давления газа вблизи резонанса. Выявлено, что начальная концентрация капель монотонно уменьшается со временем по сравнению с естественным осаждением.
Исследование выполнено за счет гранта Российского научного фонда (проект № 20-79-00144).
1.Нигматулин Р.И. Динамика многофазных сред // Москва: Наука. 1987. Т. 1. 464 с.
2.Mortell M.P., Seymour B.R. Nonlinear resonant oscillations in closed tubes of variable cross section // J. Fluid Mech. 2004. V. 519. P. 183–199.
3.Davidson G.A., Jager W. Turbulence and aerosol coagulation in high intensity sound fields // J. Sound and Vibr. 1980. V. 72. №. l. P. 123.
4.Daru V., Baltean-Carles D., Debesse P., Gandikota G. Two-dimensional numerical simulations of nonlinear acoustic streaming in standing waves // Wave Motion. 2013. V. 50. P. 955–963.
5.Аганин А.А., Кузнецов В.Б., Мартынов Е.В., Смирнов Э.Т. Экспериментальное и численное исследование акустических течений около объемных резонаторов // ПМТФ. 1997. Т. 38. № 6. С. 61-71.
6.Tkachenko L.A., Shaidullin L.R., Kabirov A.A. Acoustothermal Effect in an Open Tube with Section Leap for Nonlinear Gas Oscillations // Lobachevskii J. Math. 2020. V. 41. P. 1300–1304.
7.Gubaidullin D. A., Zaripov R. G., Tkachenko L. A., Shaidullin L. R. Deposition of polydisperse gas suspensions with nonlinear resonance oscillations in a closed tube // J. Acoust. Soc. Am. 2019. V. 145. № 1. EL30- EL33.
Линар Радикович Шайдуллин
МИРЭА – Российский технологический университет

Пространственное распространение пандемии COVID-19 изучается с помощью кинетического метода с введением двух параметров. Предлагается одномерная модель на основе уравнения кинетического типа для изучения динамической плотности распределения носителей вируса во времени и пространстве с учетом их миграции из выделенного центра. Данная модель является новой и принципиально отличается от известных моделей типа диффузия-реакции. Строится аналитическое решение; для получения серии расчетов применяются и численные методы. Производится сравнение модельных и реальных данных в Италии, России и Чили (возможность применения простой одномерной модели для этих стран связана с особенностями их географического положения). Помимо скорости заражения, вводится в рассмотрение «скорость выздоровления». При прохождении волны выздоровления по территории с большей частью населения страны делается вывод о начале глобального выздоровления, что соответствует реальным данным. Предсказания оказываются точными и для второй волны пандемии в России. Ожидается, что модель способна адекватно описать не только развитие COVID-19, но и последующих эпидемий.
Андрей Дмитриевич Ястребов
НИИ Механики МГУ им. М.В. Ломоносова
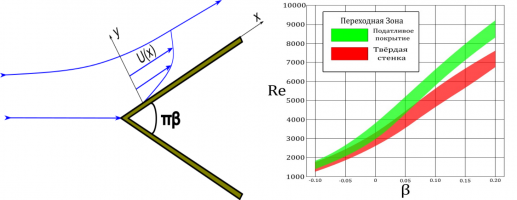
В линейной постановке исследовалась устойчивость пограничных слоев Фолкнера-Скэн над монолитным податливым покрытием. Путём решения связанной линеаризованной системы уравнений Навье-Стокса и уравнений движения вязкоупругого слоя для нормальных мод определялось наименее устойчивое собственное значение. В расчётах учитывалось изменение скорости внешнего потока в продольном направлении, использовались экспериментальные зависимости свойств покрытия от частоты [1]. При помощи метода оценивалось влияние податливого покрытия на положение области ламинарно-турбулентного перехода [2]. Расчеты показывают существенное влияние покрытия на ламинарно-турбулентный переход. Так, для течений с благоприятным градиентом давления рассматриваемое покрытие увеличивает координату конца ламинарно-турбулентного перехода на 41 %, по сравнению с увеличением на 32 % для пограничного слоя Блазиуса [3].
Исследование выполнено за счет гранта Российского научного фонда
(проект № 20–11–20141).
1. Kulik V. M., Boiko A. V., Lee I. Using two-layer compliant coatings to control turbulent boundary layer // Thermophysics and Aeromechanics. 2019. V. 26. № 1. P. 47-57.
2. van Ingen J. The eN method for transition prediction. Historical Review of Work at TU Delft // 38th Fluid Dynamics Conference and Exhibit., Seattle, June 23-26, 2008. American Institute of Aeronautics and Astronautics Inc. (AIAA), 2008. P. 1-49.
3. Ашуров Д. А. Устойчивость и переход к турбулентности в пограничных слоях с градиентом давления над монолитным податливым покрытием. // Прикладная Механика и Техническая Физика. 2021 (в печати).
Денис Абдулвагабович Ашуров